
Лекция. Элементы Векторной Алгебры
.pdfП 3.Каноническое уравнение гиперболы.
•О. Гипербола - геометрическое место всех
точек плоскости, координаты которых в некоторой прямоугольной системе координат Oxy удовлетворяют уравнению
(6.2) |
x2 |
|
y2 |
1, |
где a 0, |
b 0. |
|
a2 |
b2 |
||||||
|
|
|
|
|
•Уравнение (6.2) - каноническое уравнение
гиперболы.

•1. Координатные оси являются осями симметрии.
•2. Точки (±a,0)– вершины гиперболы.
•3. Точка О(0,0) – центр гиперболы.
•4. Прямые
гиперболы.
y ba x - асимптоты
• 5. Линейный эксцентриситет гиперболы –
число |
|
|
|
|
|
c |
a |
2 |
b |
2 |
|
|
|
|
•6. Точки F1=(-c,0), F2=(c,0) – фокусы
гиперболы.
•Свойство гиперболы :
•Теорема. Для любой точки M(x,y)
гиперболы абсолютная величина разности
расстояний от этой точки до фокусов есть
величина постоянная, равная 2a, т.е.
•| | F1M |- | F2M | |=2a.
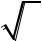
Пример.
•Через точку М(0,-1) и правую вершину
гиперболы 3x2-4y2=12 проведена прямая.
Найти вторую точку пересечения этой
прямой с гиперболой.
•Решение. Каноническое уравнение этой гиперболы:
x2 |
y2 |
|
|
|||
|
|
|||||
|
|
|
1, |
т.е. a 2,b 3 |
||
4 |
3 |
|||||
|
|
|
|
|||
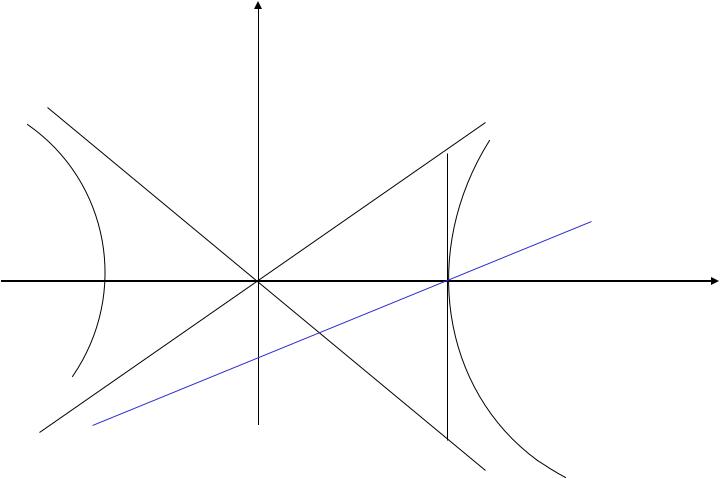
y
F2 x
M
•Правая вершина: B(2,0).
•Уравнение прямой, проходящей через М и B:
y 1 |
|
x 0 |
, |
т.е. x 2 y 2 0. |
||
0 1 |
|
2 0 |
||||
|
|
|
||||
• Точка D пересечения этой прямой с
гиперболой: |
x 2 y 2 |
||||
|
|
2 |
4 y |
2 |
12 |
3x |
|
|
|||
•3(2y+2)2-4y2=12 => 8y2+24y=0 8y(y+3)=0.
•=> y=0 , y=-3.
•Итак, yD =-3, xD =2yD +2=-4. Ответ: D(-4,-3).
П 4.Каноническое уравнение параболы.
•О. Парабола - геометрическое место всех
точек плоскости, координаты которых в некоторой прямоугольной системе координат Oxy удовлетворяют уравнению
(6.3) |
y2 2 px, где |
p 0. |
•Уравнение (6.3) - каноническое уравнение
параболы.
•1. Ось абсцисс Ox является осью
симметрии.
•2. Точка О(0,0) – вершина параболы.
•3. Число p – фокальный параметр
параболы.
•4. Точка F(p/2;0) – фокус параболы.
•5. Прямая x=-p/2 – директриса параболы.
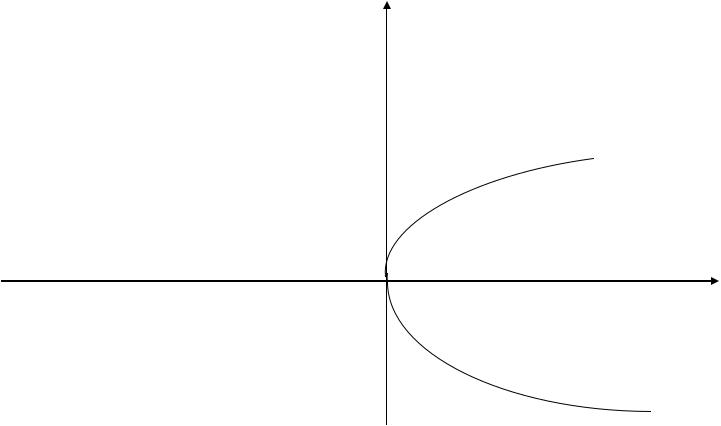
y2=2px.
y
-p/2 |
|
p/2 |
x |
|
|||
|
|
||
|
|
|
|
|
|
|
|
Свойство параболы.
•Теорема. Точка M(x,y) принадлежит параболе она равноудалена от фокуса
и директрисы.
