2. 5. Распределенные и нераспределенные термины в простых суждениях

Основные структурные элементы простого суждения - субъект и предикат - называются терминами суждения. В любом суждении каждый термин является распределенным или нераспределенным.

Термин считается распределенным (т.е. развернутым, исчерпанным, взятым в полном объеме), если в суждении речь идет обо всех объектах, входящих в объем этого термина, и обозначается знаком «+», а на круговых схемах Эйлера изображается полным кругом (т.е. кругом, который не содержит в себе другого круга и не пересекается с другим кругом:

+

Термин считается нераспределенным (т.е. неразвернутым, неисчерпанным, взятым не в полном объеме), если в суждении речь идет не обо всех объектах, входящих в объем этого термина, и обозначается знаком «-», а на круговых схемах Эйлера изображается неполным кругом (т.е. кругом, который содержит в себе другой круг или пересекается с другим кругом):

  

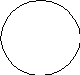
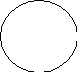
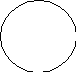
Например, в суждении: Все акулы (S) являются хищниками (Р) речь идет обо всех акулах, значит субъект этого суждения распределен. Однако, в данном суждении речь идет не обо всех хищниках, а только о части хищников (именно – о тех, которые являются акулами), следовательно, предикат указанного суждения нераспределен. Изобразив отношения между субъектом и предикатом (которые находятся в отношении подчинения) рассмотренного суждения круговыми схемами Эйлера, увидим, что распределенному термину (субъекту акулы) соответствует полный круг, а нераспределенному (предикату хищники) – неполный (попадающий в него круг субъекта как бы вырезает из него какую-то часть):

P-

Распределенность терминов в простых суждениях может быть различной в зависимости от вида суждения и характера отношений между его субъектом и предикатом. Рассмотрим все случаи распределенности терминов в простых суждениях.

1. Если в суждении вида А субъект и предикат находятся в отношении равнозначности, то они оба являются распределенными (S+, P+), например: Все квадраты (S) - это равносторонние прямоугольники (P).

S=P

2. Если в суждении вида А субъект и предикат находятся в отношении подчинения (других отношений между субъектом и предикатом в суждениях вида А, кроме равнозначности и подчинения, как мы знаем, быть не может), то субъект распределен, а предикат нераспределен (S+, P-), например: Все розы (S) являются цветами (P).

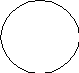
P

S

3. Если в суждении вида I субъект и предикат находятся в отношении пересечения, то они оба являются нераспределенными (S-, P-), например: Некоторые школьники (S) - это спортсмены (P).

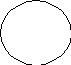
S P

4. Если в суждениях вида I субъект и предикат находятся в отношении подчинения (других отношений между субъектом и предикатом в суждениях вида I, кроме пересечения и подчинения, быть не может), то субъект нераспределен, а предикат распределен (S- P+), например: Некоторые животные (S) являются хищниками (P).

S

P

5. В суждениях вида Е субъект и предикат находятся только в отношении несовместимости. Поэтому в этих суждениях они всегда оба распределены (S+, P+), например: Все киты (S) не являются рыбами (P).

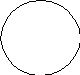
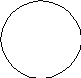
S P

6. Если в суждениях вида О субъект и предикат находятся в отношении пересечения, то, в отличие от их распределенности в суждениях вида I, субъект нераспределен, а предикат распределен (S-, P+), например: Некоторые школьники (S) не являются спортсменами (P).

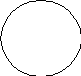
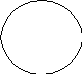
S P

Несмотря на пересекающиеся круги на схеме Эйлера, субъект данного суждения нераспределен, а предикат распределен. Почему так получается? (Выше мы говорили о том, что пересекающиеся на схеме круги обозначают нераспределенные термины). На схеме штриховкой показана та часть субъекта, о которой идет речь в суждении, а речь в нем идет о тех школьниках, которые спортсменами не являются, в силу чего круг, обозначающий на схеме предикат, остался полным (т.е. круг, обозначающий субъект, не отрезает от него какую-то часть, как это происходит в суждении вида I, где субъект и предикат находятся в отношении пересечения).

7. Если в суждении вида О субъект и предикат находятся в отношении подчинения, то субъект нераспределен, а предикат распределен (S-, P+), например: Некоторые животные (S) не являются хищниками (P).

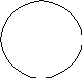
S

P

Итак, cубъект всегда распределен в суждениях вида А и Е и всегда нераспределен в суждениях вида I и О, а предикат всегда распределен в суждениях вида Е и О, но в суждениях вида А и I он может быть как распределенным, так и нераспределенным в зависимости от характера отношений между ним и субъектом в этих суждениях.