§1. Формулировка задачи.

В m сосредоточен однородный груз в количествахЭтот груз нужно перевезтиn потребителям в количествах Известны числа- стоимость перевозки единицы груза отi-го поставщика j-му потребителю (тариф перевозки).

Будем считать, что потребности в грузе равны его запасам: (задача с правильным балансом).

Обозначим - объём груза, перевозимого отi-го поставщика j-му потребителю.

Условия транспортной задачи будем записывать в виде транспортной таблицы.

bj ai	b1	b2	…	bn
a1	c11	c12	…	c1n
a2	c21	c22	…	c2n
…
am	cm1	cm2	…	cmn

Введём вектор

Х – план перевозок.

План перевозок должен удовлетворять следующим условиям

1.

1. 

Условие (1) – требование того, чтобы грузы от каждого поставщика были вывезены полностью.

2.

2. 

Условие (2) – требование того, чтобы запросы каждого потребителя были полностью удовлетворены.

3. 

Математическая формулировка транспортной задачи:

Найти такой план Х, удовлетворяющий системам ограничений (1) и (2), условиям неотрицательности (3) и обеспечивающий минимум целевой функции f.

Симплекс-процесс:

1. Определение исходного опорного решения.

2. Оценка этого решения.

3. Переход к лучшему решению путём однократного замещения одной базисной переменной на свободную.

Однако специфичность системы ограничений (1) , (2) позволяет систематизировать для её решения более простой вычислительный алгоритм, чем симплексный метод.

Особенности системы ограничений (1), (2):

1. Коэффициенты при неизвестных (1), (2) равны единице.

2. Каждая неизвестная встречается в двух и только двух уравнениях, причем одно из уравнений входит систему (1), а другое – в (2).

§2. Ранг системы уравнений транспортной задачи.

Запишем систему уравнений (1), (2) в векторной форме:

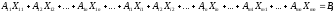
где -- - вектор-столбец коэффициентов при неизвестн.Х₁₁ в системе (1), (2).

1-я строчка

(m+n) координат

(m+1) строчка

(m+j) строчка

i-я строчка

Каждый вектор А_ij состоит из (m+n) строк. Только два элемента равны единице, остальные – нулю. Одна единица расположена в строке с номером, равным первому индексу вектора, вторая единица в строке, номер которой равен второму индексу j+m.

Теорема.

Ранг системы векторов условий транспортной задачи (*) равен (m+n-1).

Доказательство:

Надо доказать, что максимальное число линейно независимых векторов системы (*) равно (m+n-1).

Рассмотрим систему из (m+n-1) вектора:

(**)

Докажем:

1. Система (**) линейно независима.

вектор коорд. вектора	A1n	A2n	A3n	…	Amn	A11	A12	…	A1n-1
1 2 3 …	1 0 0 …	0 1 0 …	0 0 1 …	… … … …	0 0 0 …	1 0 … …	1 0 … …	… … … …	1 0 … …
m	…	…	…	…	1	…	…	…	…
m+1 m+2	… …	… …	… …	… …	0 …	1 0	0 1	… …	… …
… m+n-1 m+n	… 0 1	… 0 1	… 0 1	… … …	… 0 1	… 0 0	… 0 0	… … …	… 1 0

Составим линейную комбинацию векторов системы (**).

Выясним, при каких значениях коэффициентов вектор Y – нулевой.

Два вектора равны тогда и только тогда, когда равны их соответствующие координаты

Система имеет единственное решение .

Это означает, что только тривиальная линейная комбинация системы векторов (**) равна θ система векторов (**) линейно независима.

2. Добавим в систему (**) вектор , при этом, т.к. всеn векторов с первым индексом «1» входят в систему (*), q<n, т.к. все m векторов, у которых второй индекс равен «n», входят в систему (**).

В результате получим следующую систему векторов

(+)

вектор коорд.	Apq	-Apn	-A1q	A1n
1 … p … q+m … m+n	1 1	-1 -1	-1 -1	1 1

- нетривиальная линейная комбинация векторов - линейно зависимыевся система векторов (+) линейно зависима. Из 1) и 2)ч.т.д.

Следствие: ранг системы ограничений (1), (2) транспортной задачи равен m+n-1, т.е. число базисных неизвестных в любом общем решении системы (1), (2) равно (m+n-1).