Не разобранные / Линейное программирование / шпоры / 1-16

1.Формулировка и различные формы записи задачи линейного программирования. Найти вектор X=(x₁,x₂,…,x_n), который удовлетворяет системе линейных ограничений и обеспечивает экстремальное (минимальное или максимальное) значение целевой функции. Ограничения могут быть сформулированы в виде равенств или неравенств. В зависимости от этого различают различные формы записи задач линейного программирования. Общая форма записи ЗЛП. Дано: система линейных ограничений, в которой S равенств и (m-S) неравенств

(2) (3) Требуется найти такое решение системы (1) X=(x₁,x₂,…,x_n), которое удовлетворяет условию (2), и на котором целевая функция достигает экстремума (максимума или минимума). Симметричная форма. В ней ограничение (1) содержит только неравенства

(3) (1) i=1,2,…,m

(2) (3)

(1) i=1,2,…,m (2) Каноническая форма.Ограничение (1) содержит только равенства

(3) (1) i=1,2,…,m

(2) Определение. Вектор X=(x₁,x₂,…,x_n), координаты которого являются решением ограничений (1) и (2), называется допустимым решением ЗЛП. Множество всех допустимых решений задачи называется областью допустимых решений (ОДР). Допустимое решение X, на котором целевая функция достигает максимума или минимума, называется оптимальным решением задачи.

2.Переход от одной формы записи задачи к другой.

Теорема. Пусть дано линейное неравенство с n переменными (4)

И переменная такая, что , (6)

тогда .

Док-во: (достаточность)→: Пусть X=(α₁, α ₂,…, α _n) – решение (4), т.е. 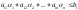(4’)

Введём α_n+1 =b_i-, (5’)

При этом . (6’)

Пусть выполняется (5’) и (6’). Отбросив в левой части уравнения (6’) , получим неравенство (4’).Теорема позволяет от неравенств в системе ограничений перейти к уравнениям и, наоборот, от уравнения перейти к неравенству.

3.Графический метод решения задачи линейного программирования.Этим методом можно решать: 1) Задачи с 2 переменными, имеющими симметричную форму записи. 2) Задачи с n переменными, имеющие канон. форму записи, если выполняется условие n-r≤2, где n – число неизвестных, r – ранг системы линейных уравнений (1).Задача типа 2 сводится к задаче типа 1, для чего нужно перейти от канонической к симметричной форме записи. Рассмотрим решение задач типа 1. Найти X=(x₁,x₂), который является решением (1), удовл. (2), (2) x₁≥0, x₂≥ 0 и на котором целевая функция f(X)=c₁x₁+c₂x₂ (3) достигает экстремума (максимума или минимума).Решение задачи содержит 2 этапа: Построим ОДР (7) Решением такого неравенства является любая пара чисел (x₁;x₂), которая при подстановке в (7) обращает его в верное числовое равенство. На координатной плоскости (x₁;x₂) – точка . Множество решений (7) – некоторое множество точек на x₁Ox₂. Выясним, какую область на плоскости x₁Ox₂ образуют точки, которые являются решением ограничений (1) и (2). Заменим неравенство (7) соответствующим ему равенством. - (8) это уравнение определяет на плоскости x₁Ox₂ прямую линию. Эта линия делит плоскость x₁Ox₂ на 2 полуплоскости π₁ и π₂. Утверждение. Точки одной из этих полуплоскостей являются решением , а точки другой полуплоскости являются решением неравенства . (**) Нахождение ОДР оптимального решения задачи.Рассмотрим уравнение (3) При конкретном значении f это уравнение определяет на плоскости прямую линию. При изменении f мы получим семейство параллельных прямых (прямые ||, т.к. они все имеют один угловой коэффициент ). Каждую из этих прямых называют линией уравнения, т.к. согласно равенству (3) на каждой такой прямой функция f сохраняет постоянное значение. Определение. Линия уровня, имеющая общие точки с ОДР и расположенная так, что ОДР целиком находится в одной из полуплоскостей, на которые данная линия уровня делит координатную плоскость, называется опорной прямой. Чтобы найти ОДР оптимального решения, выполним: 1- Строим в начале координат. 2- Перпендикулярно проводим одну из линий уровня, имеющую общие точки с ОДР. Перемещая эту линию уровня в направлении в задаче на max или в противоположном направлении в задаче на min, находим опорную прямую. Совместно решив уравнения прямых, ограничивающих ОДР и имеющих общие точки с опорной прямой, найдем оптимальное решение. В зависимости от вида ОДР и целевой функции задача может иметь единственное решение, бесконечное множество решений, или не иметь решений ввиду несовместности системы ограничений или неограниченности целевой функции ОДР.

4.Преобразование однократного замещения. Пусть дана система линейных уравнений

1. r<n (ранг системы) Приведём эту систему к разрешённому виду методом Жордано-Гаусса и выпишем общее решение системы (общее решение системы – это формулы, выражающие базисные неизвестные через свободные).Общее решение(1’)

Положив в этих формулах значение всех свободных неизвестных, равных нулю, мы найдём базисное решение системы. Исходная система (1) будет иметь не одно базисное решение, т.к. из n неизвестных можно составить разные наборы из r неизвестных, но не каждый такой набор из r неизвестных можно взять за базисные неизвестные, т.к. среди r векторов коэффициентов при этих неизвестных могут быть линейно зависимые и, следовательно, базиса из них составить нельзя. Если мы знаем какое-либо одно базисное решение, то, преобразовав систему от одного единичного базиса к другому, можем найти любое другое базисное решение системы.

5.Опорные решения. Отыскание исходного опорного решения.Определение. Опорным решением системы линейных уравнений называется базисное допустимое решение (для которого векторы условий, соответствующие положительным координатам, линейно независимы). Отыскание исходного опорного решения рассмотрим на примере. Теорема: если в системе линейных уравнений выполнить однократное замещение с разрешающим элементом a_k4, то все свободные члены уравнений системы останутся неотрицательными. Замечание. Для того чтобы найти исходное опорное решение системы линейных уравнений, надо привести систему к разрешённому виду. Если при этом все свободные члены уравнений системы будут «≥0», то базисное решение будет опорным. Если среди свободных членов уравнений разрешённой системы есть отрицательные, то следует выполнить преобразования 1) и 2). Пусть после выполнения этих преобразований все свободные члены уравнений стали неотрицательными, но i-е уравнение системы стало неразрешённым; выберем s-й столбец в таблице по положительному элементу a_is>0 в i-й строке.Найдём разрешающий элемент, согласно (*), при этом может оказаться:

1. Разрешающий элемент a_ks оказался в i-й строке, т.е. k=i.

Выполним однократное замещение с разрешающим элементом a_is, тогда i-е уравнение системы станет разрешающим относительно x_s, и все свободные члены уравнений системы будут неотрицательными, и мы сможем выписать исходное опорное решение.

2. Разрешающий элемент i-й строке, , при этом b_k>0.

Выполним однократное замещение с разрешающим элементом a_ks.

При этом свободный член i-го уравнения уменьшится, но i-е уравнение останется неразрешённым, но свободный член уменьшится. После конечного числа шагов придём к случаю 1., либо в i-м не останется положительных коэффициентов при неизвестных, что означает несовместность системы в ОДР, либо придём к случаю 3.

3. Поэтому, прежде чем выполнять преобразование однократного замещения с разрешающим элементом a_ks, нужно попробовать выбрать другой разрешающий столбец по другому положительному элементу в i-й строке. Если это сделать нельзя, то нужно выполнить однократное замещение с разрешающим элементом a_ks, тогда изменится состав базисных неизвестных, и выбор разрешающего элемента нужно будет начинать сначала. Через конечное число шагов придём к случаям 2. или 1., либо установим несовместность системы уравнений в ОДР.

6.Область допустимых решений n-мерной задачи линейного программирования. Гиперплоскость. Полупространство. Выпуклые множества.

При анализе систем линейных уравнений с n неизвестными широко используется понятие n-мерных векторов или точек n-мерного пространства. Введём n-мерное векторное (линейное) пространство Rⁿ. Элементами этого пространства являются возможные наборы из n действительных чисел, взятых в определённом порядке. - вектор или точка пространства Rⁿ. x₁,x₂,…,x_n – координаты вектора или точки. В Rⁿ определяются операции сложения элементов и умножения элементов на число.

1. X+Y=(x₁+y₁,x₂+y₂,…,x_n+y_n)

2. 

1. Вводится вектор-нуль θ=(0,0,…,0)

2. вектор, противоположный X (-X): X+(-X)=θ.

1. ***Операции I и II обладают следующими свойствами: Коммутативность X+Y=Y+X.

2. Ассоциативность сложения X+(Y+Z)=(X+Y)+Z.

3. Ассоциативность умножения , с₁,c₂ – действительные числа.

4. Дистрибутивность

А) векторная Б) скалярная

По аналогии с двух- и трёхмерными векторами в Rⁿ можно ввести понятие скалярного произведения Наличие скалярного произведения в Rⁿ позволяет ввести понятие длины вектора и расстояния между элементами Rⁿ. Длиной вектора (его модулем) наз. «» из скалярного квадрата. A(x₁,x₂,…,x_n) – каждый из которых является решением линейного уравнения относительно n переменных, называется гиперплоскостью.

A(x₁,x₂,…,x_n) – называется полупространством, расположенным по одну сторону от граничной гиперплоскости.

- коллинеарные

Параметрическое уравнение прямой m - (*)

Если , то (*) определяет прямую линию - радиус-вектор точки А из Rⁿ

- радиус-вектор точки B из Rⁿ .

Определение. Отрезком , соединяющим точки A и B, называется множество точек этого пространства, радиус-векторы которых определяются уравнением (*) Определение. Множество M называется выпуклым, если вместе с любыми своими двумя точками A и B она содержит и все точки отрезка AB, их соединяющего.

7.Теорема: пересечение выпуклых множеств есть выпуклое множество.

Пусть M₁ и M₂ – выпуклые множества и их пересечение – непустое множество , тогда - выпуклое множество.

Доказательство: Возьмём

Доказать:

Т.к. множества M₁ и M₂ – выпуклые, то

Следствие: Пересечение конечного числа выпуклых множеств – выпуклое множество.

- выпуклое множество.

M₁, M₂,..., M_n. - выпукло е

8.Теорема: область решений системы линейных уравнений и область решений системы линейных неравенств есть выпуклое множество.

Область решений системы линейных уравнений и неравенств есть выпуклое множество. Докажем, что ОР одного уравнения с n неизвестными, которое определяет гиперплоскость в Rⁿ – есть выпуклое множество. (1) . Где - вектор из неизвестных. . Пусть и - решение (1). Т.е. т. А и т. В – точки, принадлежащие ОР уравнения (1).

Возьмём любую точку С внутри [AB]. Её координаты определяются из равенства Проверим, что эта т. С также является решением уравнения (*).

Т. С является решением уравнения (1). Вместе с двумя точками А и В ОР уравнения (1) содержит все точки отрезка [AB]. ОР уравнения (1) – выпуклое множество.Докажем, что ОР одного линейного неравенства с n переменными, т.е. полупространство n-мерного пространства также есть выпуклое множество.

1. (2) - решение (2)

внутри [AB] и проверяем, что эта точка также является решением (2)

т. С является решением (2) и все точки отрезка [AB] принадлежат полупространству, которое определяется неравенством (2).

9.Угловые точки выпуклого множества. Выпуклые многогранники. Область решений системы из линейных уравнений и неравенств есть выпуклое множество. Эта область есть пересечение конечного числа гиперплоскостей и полупространств, и по теореме 2 – есть также выпуклое множество. Следствие. ОДР ЗЛП – есть выпуклое множество. Во всяком выпуклом множестве можно выделить внутренние, граничные и угловые точки. Т. А называется внутренней точкой множества М, если существует окрестность этой точки, которая принадлежит множеству М. Т. А – внутренняя точка множества М, если А – граничная точка множества М, если имеются как точки множества М, так и точки, не принадлежащие этому множеству М.

Т. А – угловая точка выпуклого множества М, если она не является внутренней ни для какого отрезка, соединяющего две другие точки множества. Множество, содержащее все свои граничные точки, называется замкнутым.

Множество М, называется ограниченным, если , что для каждой точки

Множество может быть замкнутым, но неограниченным и наоборот. Например: гиперплоскость - замкнутое неограниченное множество.

Определение. Выпуклое множество, являющееся пересечением конечного числа полупространств, называется выпуклым многогранником. Т.к. полупространство определяется линейными неравенствами, то можно сказать, что выпуклый многогранник – это множество, которое определяет конечная система линейных равенств. Т.о При решении n-мерной ЗЛП удобно использовать каноническую форму записи. Т.к. систему линейных неравенств (1) можно заменить эквивалентной ей системой линейных уравнений, то мы приходим к выводу, что областью допустимых решений n-мерной ЗЛП является n-мерный выпуклый многогранник, поэтому геометрически ЗЛП – есть задача отыскания максимума (минимума) линейной функции на выпуклом многограннике.

10.Теорема о существовании опорного решения. (без доказательства) Опор. (базис.) реш-ем нзв такое допуст.реш-е Х=(х₁, х₂,…,х_м, 0,…,0), для кот.в-ра условий, соотв.положит.коорд-там А₁, А₂, … , А_м, явл.лин.независ.системой в-ров («допуст.базисное реш-е») *Базисом опор.реш-я нзв базис системы в-ров-условий (А₁-А_м), влюч.в свой состав в-ра, соотв.отличным от 0 коорд-там опор.реш-я. ***Теорема: любое опор.реш-е есть угловая точка ОДР. И наоборот: любая угловая точка ОДР есть опор.реш-е. Каждое опорное решение явл базисным, но не каждое базисное явл опорным. Если система линейных уравнений имеет хотя бы одно допустимое решение, то среди этих решений есть хотя бы одно опорное. Доказательство: Систему линейных уравнений (1) запишем в векторной форме Где А₁ – вектор-столбец из коэффициентов при неизвестных .

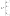
Пусть ранг векторов системы . Для определённости будем считать, что первые n векторов этой системы образуют базис. Это означает, что существует общее решение системы (1), где - базисные, - свободные; сущ. базисн. реш. . (2) Последние n-r координат вектора равны нулю.

Если первые координаты вектора неотрицательны, то это базисное решение является ещё и опорным решением системы (1). По условию теоремы 1 существует хотя бы одно допустимое решение системы (1).

1. Возможны следующие два случая: , - опорное. Т.к. n-r последних координат X₁ равны нулю X₁ – базисное решение. Кроме того, первые r координат неотрицательны

2. . В этом случае X₁ – допустимое решение, но не базисное, т.к. число последних нулевых координат меньше, чем k-r.

Т.к. X₁ – решение, поэтому (а)

Отметим, что система векторов линейно зависима, т.к. в этой системе число векторов k>r - ранг системы векторов , значит, существует нетривиальная линейная комбинация.

11.Теорема о связи между угловыми точками области допустимых решений задачи линейного программирования и опорными решениями (без доказательства) Допустимое решение ЗЛП является угловой точкой ОДР тогда и только тогда, когда это решение – опорное.

Пусть дана ЗЛП и пусть системы ограничений (1) и (2) определяют выпуклый многогранник М. Пусть - угловая точка М все

1. тогда из теоремы 1 мы получаем, что это решение является опорным.

2. (а)

- лин. завис. (б) Уравнение (а) ± уравнение (б) t, t – число, большее нуля.

Подберём число t так, чтобы все координаты векторов X₁ и X₂ были неотрицательными.

1. с₁>0 Из первого неравенства системы получаем, что .

Из второго неравенства системы получаем, что .

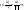
2. с₁<0 Если то первые координаты будут неотрицательными.

Решив систему , (*) найдём отрезок [-t₂,t₂], для каждой точки которого выполняется неравенство (*). Выполним этот процесс для всех ненулевых координат векторов X₁ и X₂. Найдём k чисел t₁,t₂,…,t_k. Среди этих чисел возьмём наим. тогда на [-t_i,t_i] все координаты X₁ и X₂ будут неотрицательными, это означает, что X₁ и X₂ принадлежат ОДР, т.е. это две точки многогранника М. это означает, что точка X – середина отрезка, концами которого являются т. X₁ и т. X₂, т.е. т. X не является угловой точкой по определению угловой точки. Получим противоречие, т.к. т. X – угловая по определению.

12.Выпуклая линейная комбинация системы векторов. Теорема о совпадении множества точек ограниченного n-мерного многогранника с множеством выпуклых линейных комбинаций его угловых точек (формулировка). Определение. Пусть X₁,X₂,…,X_s – система n-мерных векторов . - числа:

1. 

2. 

- выпуклая линейная комбинация системы векторов Х₁,…,X_s.

Примеры: 1-) - выпуклая линейная комбинация. 2) - не выпуклая линейная комбинация. 3) - не выпуклая линейная комбинация.

Теорема 3. Множество точек ограниченного выпуклого n-мерного многогранника совпадает с множеством выпуклых линейных комбинаций его угловых точек.

Без доказательства. Теорема содержит два утверждения: Если х₁,х₂,…,х_s – угловые точки многогранника М, то любая точка х из многогранника М.

1. .

2. Любая точка х, определяемая равенством (1) при условии, что х₁,х₂,…,х_s – угловые точки многоугольника М

Например, отрезок – многогранник, порождённый двумя точками (своими концами) и т.д. Существенно то, что многогранник – ограниченный, для неогран. теорема не выполняется.

12.Основная теорема об экстремумах линейной функции задачи линейного программирования. Теорема 1. Если ОДР ЗЛП – ограниченная, то оптимальное решение ЗЛП существует и совпадает хотя бы с одним из опорных решений системы линейных уравнений (1) – ограничений. Доказательство: Доказать, что Х – опорное решение. Пусть х₁,х₂,…,x_s – угловые точки (опорные решения) ОДР, тогда