Не разобранные / Линейное программирование / шпоры / 25-26

Теорема 1. Если ОДР ЗЛП – ограниченная, то оптимальное решение ЗЛП существует и совпадает хотя бы с одним из опорных решений системы линейных уравнений (1) – ограничений.

Доказательство:

Т.к. ОДР – ограниченная, то по второй теореме Вейерштрасса непрерывная функция на замкнутом и ограниченном интервале принимает максимальное и минимальное значение.

Пусть х – допустимое решение.

Доказать, что Х – опорное решение.

Пусть х₁,х₂,…,x_s – угловые точки (опорные решения) ОДР, тогда

(*)

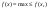Поскольку Х – допустимое решение, то для любой точки х

Т.к. x_k – допустимое решение, то (**)

Из (*) и (**):

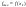
Теорема 2. Если ОДР ЗЛП – ограниченная, а функция не ограничена сверху (снизу), то задача отыскания максимума f (минимума f) не имеет решений.

Min f (max f) существует и достигается по крайней мере в одном из опорных решений.

Без доказательства.

Теорема 3. Если max (min) достигается в нескольких опорных решениях х₁,х₂,…,х_l, то любая выпуклая линейная комбинация оптимальн. опорн. реш. есть также оптимальное решение.

Доказательство:

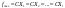
Рассмотрим вектор Y, который является линейной комбинацией оптим. реш.

Теорема доказана.

Теоремы 1,2,3 можно обобщить в основную теорему линейного программирования.

Основная теорема: если ЗЛП имеет оптим. реш., то оно совпадает, по крайней мере, с одним из опорных решений системы ограничительных уравнений.

Основная теорема указывает схему, которая может быть использована при решении ЗЛП.

Схема решения ЗЛП.

1. Найти все опорные решения.

2. Подсчитать значения линейной функции на каждом опорном решении.

3. Сравнивая найденные значения, установить опорн. реш.

Недостаток схемы: нужно исследовать каждое опорное решение.

Эта схема предполагает беспорядочный перебор опорных решений.

Симплексный метод предполагает упорядоченный перебор опорных решений так, что на каждом следующем опорном решении значение функции ближе к оптимальному решению, чем предыдущее (идея последовательного улучшения решения).

Три элемента симплексного метода:

1. Нахождение исходного опорного решения.

2. Правило перехода к следующему, лучшему опорному решению.

3. Критерий, который позволяет установить оптимальность опорного решения или необходимость его дальнейшего улучшения, или отсутствия решения.