§5. Преобразование однократного замещения.

Пусть дана система линейных уравнений

1. 

r<n (ранг системы)

Приведём эту систему к разрешённому виду методом Жордано-Гаусса и выпишем общее решение системы (общее решение системы – это формулы, выражающие базисные неизвестные через свободные).

Общее решение

(1’)

Положив в этих формулах значение всех свободных неизвестных, равных нулю, мы найдём базисное решение системы.

Исходная система (1) будет иметь не одно базисное решение, т.к. из n неизвестных можно составить разные наборы из r неизвестных, но не каждый такой набор из r неизвестных можно взять за базисные неизвестные, т.к. среди r векторов коэффициентов при этих неизвестных могут быть линейно зависимые и, следовательно, базиса из них составить нельзя. Если мы знаем какое-либо одно базисное решение, то, преобразовав систему от одного единичного базиса к другому, можем найти любое другое базисное решение системы.

Пример.

Дана система линейных уравнений, приведённая к единичному базису. Требуется преобразовать её к какому-либо другому единичному базису.

Базисные неизвестные	x1	x2	x3	x4	x5	bi	Базисное решение
x1,x4,x5	0 0 1	0 -3 1	5	0 1 0	1 0 0
	0 0	0 -3	5 1	0 1 0	1 0 0
x3,x4,x5			0 0 1	0 1 0	1 0 0

Для того чтобы найти какой-либо другой единичный базис, возьмём за разрешающий элемент любой неравный нулю коэффициент при каком-либо свободном неизвестном и выполним одну итерацию методом Жордано-Гаусса.

Свободное неизвестное x₃ стало базисным, а базисное неизвестно x₁ стало свободным. Такое преобразование называется преобразованием однократного замещения, т.к. произошло замещение базисного неизвестного x₁ свободным неизвестным x₃. Т.о. данная система уравнений преобразована к новому единичному базису, в котором вектор-коэффициенты при x₃,x₄,x₅. Последовательно выполняя преобразования однократного замещения, можно найти все базисы векторов коэффициентов и все базисы решений данной системы.

Замечание.

Для данной системы уравнений нельзя в качестве базисных неизвестных взять набор x1,x2,x4, т.к. им соответствуют вектор-коэффициенты , которые линейно зависимы, т.к. А₁-А₂-3А₄=θ.

§6. Опорные решения. Отыскание исходного опорного решения.

Определение.

Опорным решением системы линейных уравнений (1, §5) называется базисное допустимое решение (для которого векторы условий, соответствующие положительным координатам, линейно независимы). Отыскание исходного опорного решения рассмотрим на примере.

Пример.

Найти исходное опорное решение системы уравнений.

1. 

Система уравнений приведена к единичному базису.

Выпишем базисное решение:

.

Это базисное решение не является допустимым, т.к. x₁=-1<0, x₂=-4<0, x₇=-1<0.

Поэтому это базисное решение не является опорным. Это происходит от того, что в данной разрешённой системе (1) среди свободных членов есть отрицательные.

Выполним следующие два преобразования:

1. Среди свободных отрицательных членов найдём наибольший по модулю (-4).

Из уравнений (1) и (4) системы линейных уравнений вычтем уравнение (2)

2. 

В результате этого преобразования свободные члены уравнений (1) и (3) стали положительными, и эти уравнения остались разрешёнными относительно неизвестных x₁ и x₇ соответственно.

2. Умножим уравнение (2) на (-1) в системе (1). В результате преобразований 1 и 2 все свободные члены уравнения системы стали положительными, но при этом второе уравнение системы стало неразрешённым, т.к. неизвестное x₂ вошло в уравнение 1 и 3 с коэффициентом (-1) и в уравнение (2) с коэффициентом (-1) после второго преобразования.

Теперь мы должны второе уравнение разрешить относительно какой-либо переменной так, чтобы члены всех уравнений системы (2) остались неотрицательными.

Утверждение.

Если система линейных уравнений содержит уравнение , (*) в котором всето система линейных уравнений не имеет неотрицательных решений (несовместна в ОДР).

Доказательство:

Предположим противное:

Существует неотрицательное решение системы линейных уравнений . Тогда должно выполняться числовое равенство, но это числовое равенство невозможно, т.к. левая часть уравнения «≤0», а правая часть «>0».

Получили противоречие предположение о существовании такого вектораX неверно.

Систему линейных уравнений (2) запишем в виде таблицы.

x1	x2	x3	x4	x5	x6	x7	b
1 0 0 0	-1 -1 0 -1	0 0 1 0	3 4 4 2	-2 -3 -2 -1	3 1 3 0	0 0 0 1	3 4 10 3	3:3=1 4:4=1 10:4= 3:2=
1 0 0 0	-1 0 -1	0 0 1 0	3 1 4 2	-2 -2 -1	3 3 0	0 0 0 1	3 1 10 3
1 0 0 0		0 0 1 0	0 1 0 0			0 0 0 1	0 1 6 1

Во втором уравнении системы (2) найдём какой-либо положительный элемент; если такого элемента не существует, то это будет означать в соответствии с утверждением несовместность с ОДР.

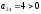
Тем самым четвёртый столбец таблицы стал разрешающим.

Определим разрешающую строку. Для этого для положительных элементов четвёртого столбца вычислим отношение свободных членов (стоящих в той же строке) к этим положительным элементам.

Пусть (*)

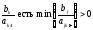Теорема: если в системе линейных уравнений (2) выполнить однократное замещение с разрешающим элементом a_k4, то все свободные члены уравнений системы останутся неотрицательными.

Доказательство:

Возьмём любой свободный член b_p и покажем, что он остаётся неотрицательным.

a_p4 b_p

a_k4 b_k

1. a_p4<0, тогда (после выполнения итерации)=

2. a_p4≥0, тогда =

В таблице (2) в первой и во второй строке мы возьмём за разрешающий элементa=4, находящийся во второй строке.

Выпишем опорное решение .

Замечание.

Для того чтобы найти исходное опорное решение системы линейных уравнений, надо привести систему к разрешённому виду. Если при этом все свободные члены уравнений системы будут «≥0», то базисное решение будет опорным.

Если среди свободных членов уравнений разрешённой системы есть отрицательные, то следует выполнить преобразования 1) и 2).

Пусть после выполнения этих преобразований все свободные члены уравнений стали неотрицательными, но i-е уравнение системы стало неразрешённым; выберем s-й столбец в таблице по положительному элементу a_is>0 в i-й строке.

Найдём разрешающий элемент, согласно (*), при этом может оказаться:

1. Разрешающий элемент a_ks оказался в i-й строке, т.е. k=i.

Выполним однократное замещение с разрешающим элементом a_is, тогда i-е уравнение системы станет разрешающим относительно x_s, и все свободные члены уравнений системы будут неотрицательными, и мы сможем выписать исходное опорное решение.

2. Разрешающий элемент i-й строке, , при этомb_k>0.

Выполним однократное замещение с разрешающим элементом a_ks.

a_is b_i

a_ks b_k

При этом свободный член i-го уравнения уменьшится, но i-е уравнение останется неразрешённым, но свободный член уменьшится.

После конечного числа шагов придём к случаю 1., либо в i-м не останется положительных коэффициентов при неизвестных, что означает несовместность системы в ОДР, либо придём к случаю 3.

3. Поэтому, прежде чем выполнять преобразование однократного замещения с разрешающим элементом a_ks, нужно попробовать выбрать другой разрешающий столбец по другому положительному элементу в i-й строке. Если это сделать нельзя, то нужно выполнить однократное замещение с разрешающим элементом a_ks, тогда изменится состав базисных неизвестных, и выбор разрешающего элемента нужно будет начинать сначала. Через конечное число шагов придём к случаям 2. или 1., либо установим несовместность системы уравнений в ОДР.