20. Теорема Штейница и следствие.

Пусть даны две сист. векторов - в₁,в₂,в₃….в_m (1) и a₁,a₂,a₃….a_n (2). Каждый вектор сист (1) линейно выражается через векторы сист (2). Тогда если m>n, то векторы сист (1) Лин Зав.

Док: По условию каждый вектор сист (1) линейно выражается через векторы сист (2)

в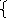₁= к₁₁а₁+ к₁₂а₂+…+к_1nа_n к₁₁…..к_mn – известные числа сист (1)

в₂= к₂₁а₁+ к₂₂а₂+…+к_2nа_n (3)

в_m= к_m1a₁+ к_m2а₂+…+к_mnа_n

λ₁в₁+λ₂в₂+….+λ_mв_m= λ₁(к₁₁а₁+к₁₂а₂…+к_1nа_n)+ λ₂ (к₂₁а₁+к₂₂а₂…+к_2nа_n)+…+ λ_m(к_m1а₁+к_m2а₂…+к_mnа_n)= θ =>(равносильно)

λ₁к₁₁+λ₂к₂₁+…+λ_mк_m1=0

λ₁к₁₂+λ₂к₂₂+…+λ_mк_m2=0 (3)

λ₁к_1n+λ₂к_2n+…+λ_mк_mn=0

Сист. 3-система однородных уравн. относительно λ₁, λ₂… λ_m, где m-неизвестных и n-уравн. Т.к. m>n=>система уравн неопределенна и сущ нетривиальные решения=>сущ нетривиальные лин комбинации сист (2) = θ. Следствие: Пусть сист векторов (1) – ЛЗ и каждый вектор сист разлагается по векторам сист (2), тогда n≥m Док: Предположим, что n<m тогда сист (1) – ЛЗ (по??????),но это не так.

14. Векторная форма записи системы линейных уравнений.

Пусть дана система m лин. ур-ий с n неизв.

(1)

Введем m-мерные векторы коэф-тов:

Каждая коорд. вектора- коэф-т при неизв.вi-ом ур-е сис-мы (1).

Введем вектор , каждая коорд. которого есть свободн. член соотв. ур-я.

Теперь сис-му (1) можно записать в виде векторн. ур-я: (2)

Утверждение: - реш-е ур-я (2) тогда и только тогда, когда- реш-е (1)

Док-во:

1) Пусть - реш-е ур-я (2). Подставимв лев. часть ур-я (2):

(3)

Вектор (3)=вектору (из (2)). Из равенства 2-х этих векторов следует равенство для всехn координат этих векторов:

(4)

Равенства (4) означают, что явл. реш-ем сис-мы (1).

2) Пусть вектор явл. реш-ем сис-мы (1), т.е. выполняется равенства (4), котор. равносильны рав-ву 2-хn-мерных векторов: вектора, записанного под (3) и . Т.е. получаем, откуда след., чтоявл. реш-ем векторн. ур-я (2), которое будем называть системой лин. ур-й.

24.Теорема Кронекера – Капелли (доказать)

Теорема: Система совместна тогда и только тогда , когдат ранг векторов коэф-ов равен рангу расшир. Сист векторов

r=r1

Док-во(необходимое)

Пусть дана система:

x1+x2+…+ xn = (1)

Пусть она совместна(ранги совпадают, сущ. Реш-е) допустим:

=( ) – реш-е сист (1)

Пусть k1a1+k2a2+…+ knan= лин. Выражается через векторы-коэф. Сист (1), ранг ()=r

добавим вектор b: (,,…,), получим расшир систему

ранг (,…,)=r по Т. так как в лин. Выраж через (,…)

Док-во (достаточное)

Пусть r=r () ,базис сист векторов-коэф. А значит и базис сист. Векторов

=k1 +k2 +…+ kr ↔↔(k1,k2…kr,0,…,0) – реш-е сист (1) ⇒ сист (1) совместна.

21- Теорема: Каждый базис данной системы векторов включает одно и то же кол-во векторов.

Док-во: Пусть дана сис-ма векторов ;- базис (I), - базис (II). Доказать: s=m.

Т.к. (II) – базис, по опр. каждый вектор сис-мы (I) разлагается по базису (II). С другой стороны, векторы сис-мы (I) лин. незав. Тогда по следствию из т. Штейнца .

Векторы сис-мы (II) лин. незав. и каждый вектор сис-мы (II) разлагается по векторам (I), => по следствию . =>,- такое возможно, только еслиs=m, ч.т.д.