шпоры по матану
.doc|
1.Функция, математ., если две переменн. величины связаны условиями вопроса так, что только одной из них можно давать произвольн. значения, а соответствующие значения другой получатся из заданной зависимости между переменными, то первая переменная наз. независимой, а вторая зависимой или ее функцией; обозначается это так y=f (x), где x независим. переменная; у—функция. Например, площадь круга есть функция его радиуса. Если зависимость Ф. от перемен. независимых выражена при помощи конечного числа алгебраическ. действий (сложение, вычитание, умножение, деление, возвышение в степень и извлечение корня), то такая Ф. наз. алгебраической, все остальные Ф. наз. трансцедентными. Алгебраич. Ф. делятся на рациональные и иррациональные; рациональная Ф. может быть целой и дробной, из трансценд. Ф.— показательные, логарифмические, тригонометрические и эллиптические. 3. Определение предела последовательности. последовательностей. Последовательности. Предел последовательности. Пусть N-множество натуральных чисел n=1, 2, 3… . Если задано отображение множества натуральных чисел N в множество действ.чисел R, то говорят, что задана последовательность. Опр:Число А-предел последовательности { an },если для всех ξ>0 нер-во │ an -А│<ξ выполняется.начиная с некоторого N,т.е. все n≥N. n→∞ n→∞ Опр-е предела ф-ии в точке.Примеры.Св-ва пределов ф-ии. Опр-е:пусть f(x) задана проколотой окр-ю точки х=а.Число b наз-ся пределом f(x) при х→а если нер-во ׀f(x)-b׀‹E,Е‹0.Выполняется для всех хєUб^0(а) для некоторых б. Примеры:1)f(x)=c limf(x)=c х→а док-во:׀f(x)-b׀‹Е (выполняется для всех х) ׀с-с׀‹Е 0‹Е 2)f(x)=x limf(x)=a x→a док-во: ׀f(x) -b׀‹E ׀x-a׀‹E при х є U(a),т.е. при х 0‹׀x-a׀‹б если б=Е док-во выполнено.3)f(x)=x^2/х f(x)=x,если х≠0 или х=0 не опред. Рассмотрим f1(x)=x(при всех х) Ф-я f1(x) отличается в 1-ой единственной точке,а именно в т. х=0.Согласно замечанию(факт существования/отсутствия предела не изменится если изменить знач-я ф-ии в т. х=а),кот следует из опр-я,мы можем утверждать,что пределы этих ф-ий при х→0 одинаковы.limx→0x^2/x=limx→0 x=0. 4.Непрерывность ф-ии в точке.Теорема о непрерывности злементарных ф-ий.Правило вычисления предела непрерывной ф-ии. Пусть ф-я определена в некот окр-ти т. а и в самой т. а.Если справедливо рав-во:limx→af(x)=f(a),то f(x) наз-ся непрерыв в т.а. Все ф-ии,кроме ф-ии у=׀х׀ наз-ся элементарными. Т: все элементарные ф-ии непрерывны в любой точке из области опр-я если ф-я определена в некоторой двусторонней окр-ти этой точки.Замечание:ф-я у=׀х׀ непрерывна в любой точке. Правило...:для того чтобы подсчитать знач-е непрерыв ф-ии над выч-ть знач-е этой ф-ии в т. а. 5. Бесконечно малые последовательности и их свойства. Опр: {an} б/м если an →0. Примеры:1/n;1/2n ;arcctg x. Св-ва: 1)всякая сходящаяся послед-ть может быть представлена в виде суммы своего предела и беск/мал посл-ти.Док-во: xn=а+ ( xn -а),где ( xn -а) это αn.Проверим,что αn беск/мал,т.е. limn→∞( xn -а)=0. Для этого рассмотрим │( xn -а) -0│<ξ (*)→выполняется для всех n≥N,т.к. limn→∞xn=а(по усл.).Значит,и (*) выполняется для всех n≥N,т.е. ( xn -а)= αn 2)сумма беск/мал послед-тей есть беск/мал посл-ть. 3)произведение беск/мал и ограниченной посл-тей явл-ся беск/мал посл-тью.Следствие:произведение беск/малых есть беск/малая посл-ть. Т.к. хn– б.м. => хn огранич (т.к. сходящаяся посл-сть оганич ) (св-во 1) Тогда по св-ву 3 хn* уn – б.м. посл-сть. 6. Арифметические действия с пределами. Теорема. Пусть lim x = a , lim у = b , тогда: Пусть limn→∞xn=а и limn→∞yn=b.Тогда 1) limn→∞(xn±yn)=а±b 2)limn→∞(xnyn)=аb Док-во:представим xn=а+ αn(беск.мал), yn=b+βn(беск.мал) тогда xnyn=(а+αn)(b+βn)=ab(число)+αnb(б/ м и огран)+ βna(б/ м и огран)+ αn βn(б/ м и огран).Т.к. xnyn=число+б/м,то limn→∞(xnyn)=число.3)если yn≠0 и b≠0,то limn→∞(xn/yn)=а/b 3) Если у ≠ 0 для любого n и b ≠ 0, то lim xn/уn= а / b n Следствие: 1) 1/ n² , 1/ n³ – б.м. , т.к. 1/ n² = 1/ n * 1/ n
2) (-1)ⁿ / n – б.м. , т.к. (-1)ⁿ * 1/ n
3) sin n / n = sin n * 1/ n – беск.мал.
|
7.Первый и второй замечательные пределы. А)limx→0(1+x)1/x=e limx→a(1+α(x))1/α(x)=e, если α(х)→0 при х→а. Док-во: limx→0sinx/x=limx→0x/sinx=1. пусть х є (0;π/2) Рассмотрим сектор АОС Sкр=πr^2=π (т.к r =1)→2π радиан, Sсек=у →х радиан У=Sсек=πх/2π=х/2 SАOC<SсекАОС<SBOC 1/2*1*sinx≤x/2≤1/2*1*1*tgx (*)1<x/sinx<1/cosx,х є (0;2π) х=-у след-но у є (-π/2;0) 1<-y/sin(-y) < 1/cos(-y) 1<y/siny<1/cosy y є(-π/2; 0) Отсюда с учетом нер-ва(*) получаем (**) 1<x/sinx<1/cosx,х є (-π/2;0)υ(0;π/2). Т.к 1/cosx стремится к 1/cosx=1,то из нер-ва(**) по теореме о пределе пром ф-ии limx→0 x/sinx=1 2ой зам пред: limx→aα(x)/sin(α(x))= limx→asinα(x)/α(x)=1 если α(х)б.м. при х→а Предел отношения sin малого угла к самому этому углу,а также предел обраного отношения=1.
8.Производная ф-ии в точке.Линейные операции и производная. Пусть ф-я определена в некотор двусторон окр-ти т.х0. ∆х-приращение аргумента.∆f=f(x0+∆x)-f(x0) Предел отношения приращ-я ф-ии к приращению аргумента когда приращение аргумента→0 наз-ся производной ф-ии. lim∆x→0∆f/∆x=f′(x0)
9.Вывод правил вычисления производных произведения и частного. Пусть даны 2 ф-ции f(x) и g(x), определенные в А и имеющие конеч.производные в т.хА. Тогда композиция этих функций h(x) вида: f*g и f/g (g(x)≠0) – также имеет конеч.производную в т.х, равную f’g+fg’ и f’g-fg’/g² соответственно.
f*g=1/2((f+g)²-f²-g²) (f*g)’=1/2[((f+g)²)’-(f²)’-(g²)’]=1/2[2(f+g)(f’+g’)-2ff’-2gg’]=1/2[2ff’+2fg’+2gf’+2gg’-2ff’-2gg’]=fg’+gf’
(f/g)’=(f*(1/g))’=f’*(1/g)+f*(1/g)’=f’/g-fg’/g²=(f’g-fg’)/g². 10-11.Вывод производных для ф-ий x^2,1/х,sinx,cosx. 1)f(x)=x2 ∆f=(x0+∆x)2-x02 =2x0*∆x+(∆x)2=∆x(2x0+∆x) ∆f/∆x=2x0+∆x lim∆x→0∆f/∆x=2x0 (x2)′=2x0 f(x)=1/x ∆f=1/(x0+∆x)-1/x0=-∆x/x0(x0+∆x) ∆f/∆x=-1/x0(x0+∆x) lim∆x→0=-1/x02 f(x)=sinx ∆f=sin(x0+∆x)-sinx0=2sinx((x0+∆x)-x0)/2*cos(2x0+∆x)/2=2sin∆x/2*cos(2x0+∆x)/2 f′(x0)=(2sin∆x/2*cos(2x0+∆x)/2)/∆x=lim(sin∆x/2cos(2x0+∆x)/2)/∆x/2=cosx0 f(x)=cosx ∆f=f(x0+∆x)-f(x0)=cos(x0+∆x)-cosx0=-2sin(2x0+∆x)/2*sin∆x/2 ∆f/∆x=(-2sin(2x0+∆x)/2*sin∆x/2)/∆x=(-sin(2x0+∆x)/2*sin∆x/2)/∆x/2 lim∆x→0∆f/∆x=-sinx0 12.Вывод производных для ф-ий lnx,logax, (lnx)′=1/x ∆f/∆x=(ln(x+∆x)-lnx)/∆x=1/∆x*ln(x+∆x)/x=1/x*x/∆x*ln(1+∆x/x)=1/x*ln(1+∆x/x)x/∆x=1/x*lne=1/x (logax)′=(lnx/lna)′=(1/lna*lnx)′=1/lna*1/x=1/xlna (ex)′=ex ∆f/∆x=(ex+∆x-ex)/∆x=(ex(e∆x-1))/∆x = пусть е∆х=1+t t→0 если ∆х→0 ∆х=ln(1+t) =(ex(t))/ln(1+t)=ex*1/(1/t*ln(1+t)) limt→0ex*1/(1/t*ln(1+t))=limt→0ex/ln(1+t)1/t=ex 13. Формула производной сложной функции. Примеры Пусть даны ф-ции y=f(u), определенная в В, и u=φ(x), определенная в А, имеющие конечные производные в u0 и x0. Тогда F(x)=f(φ(x)) имеет производную в т.х0, равную F’(x0)=f(φ(x0))’=f’(u0)φ’(x0)
Степенная ф-ция xp (x>0, pR)
14. Вывод производной для функции xp. Степенная ф-ция xp (x>0, pR)
15. ex,ax (ax)′=ax*lna ∆f/∆x=(ax+∆x-ax)/∆x=(ax(a∆x-1))/∆x= Пусть а∆х-1=t t→0 если ∆х→0 a∆x=t+1 ∆x*lna=ln(t+1) ∆x=(ln(t+1))/lna ax*(tlna)/(ln(1+t))=ax*lna*1/(1/t*ln(1+t))=axlna
|
16. Вывод производных для функций tgx, ctgx.
Взаимно обратные ф-ции и их свойства. Производная обратной ф-ции. 1. f(x), g(x) – взаимно обратные, если обл.значений одной из них совпадает с областью определения другой и наоборот. D(f)=E(g) E(f)=D(g) 2. f(a)=b g(b)=a Осн.св-ва: 1. Графики взаимно обр.ф-ций симметричны относительно прямой у=х. 2. g(f(x))=x, xD(f) f(g(x))=x, xD(g) Примеры:
Пусть f и g взаимно обр.ф-ции и известна производная f’(x). Найдем производную g’(x). f(g(x))=x, xD(g) (f(g(x)))’=1 f’(g(x))g’(x)=1 => g’(x)=1/f’(g(x)) 17. Вывод производных обратных тригонометрических ф-ций. arcsinx=g(x)
18.
Производные высших порядков Если
функция f
(x)
дифференцируема при всех x
є (a;
b)
, то мы можем рассмотреть функцию
если эта производная
существует. n-я
производная называется также производной
n-го
порядка, а
её номер n
называется порядком
производной.
При
|
19. Теорема Ролля
Пусть функция
Замечание
5.2 Это
утверждение можно переформулировать
так: между двумя корнями a
и b
дифференцируемой функции
Рис.5.4.Между двумя корнями дифференцируемой функции лежит хотя бы один корень её производной
Доказательство
теоремы Ролля: Tак
как при наших предположениях функция
Если же
|
||||||||||||
|
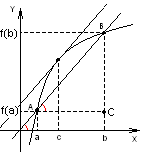
20. Теорема Лагранжа и ее геометр.смысл Пусть f(x) определена на отр.AB,имеет произв-ю в инт-ле (a,b) и непрерыв.слева в т.А, а справа в т.В. Тогда внутри инт-ла АВ найдется т.С, для к-рой справедливо рав-во: f’(C)*(b-a)=f(b)-f(a) Геометр.смысл:
Теорема утверждает, что найдется т.С внутри инт-ла АВ, касат-ная в к-рой || хорде АВ. Д-во: введем вспомогательную ф-ю
Она непрерывна на [a,b] как сумма непрерыв.ф-й, имеет производную
в (a,b)
и F(a)=F(b)=0.
=>
При х=с
21. Правило Лопиталя для раскрытия неопределенностей (0/0, /, 0, -, 1, 0, 00) Если имеется неопред-ть вида 0/0 или /, то предел отношения ф-ий можно заменить пределом отношения их производных. Теорема: Если 1)ф-ии f(x) и g(x) заданы в проколотой окрест-ти т.х0; 2)в этой окрест-ти сущ.производные f’(x) и g’(x); 3) g’(x) ≠0, g(x)≠0; 4) f(x) и g(x) обе либо беск. малые, либо беск.большие (при хх0), тогда справедливо равенство
Замечание1: Правило Лопиталя можно исп.для вычисления одностор.пределов, а также при х() Замечание2: Если lim(f’(x)/g’(x)) не сущ., то правило неприменимо. xx0 Пример:
22. Монотонные ф-ии. Признак монотонности. Ф-ия f(x) нзв монотонно возрастающей (убывающей), если х и x’А выполняется усл-е: x<x’ =>f(x)<f(x’) (или f(x)>f(x’)). Если фунуциональное рав-во выполняется нестрого, f(x) нзв неубывающей (или невозраст.). Св-во монотонности может проявляться либо на всем множ-ве А, либо на отдельных подмнож-вах. При этом на одних участках ф-ия может возрастать, а на других – убывать. Теорема. Если f’(x)>0 при x(a,b),то f(x) возрастает. Если f’(x)<0 при x (a,b),то f(x) убывает. Д-во: рассмотр.произв.точки x1 и x2 из инт-ла (a,b). х1<x2. Напишем теорему Лагранжа для a=x1 и b=x2. f(x2)-f(x1)=f’(c)*(x2-x1), c(x1,x2) >0 >0 f(x1)-f(x2)>0 => f(x2)>f(x1), т.е. f(x) возрастает. Аналогично для убывающ.ф-ии f(x2)<f(x1) при x1<x2. 23. Экстремум ф-ии y=f(x). Необходимое усл-е экстремума.Ф-ия y=f(x), определенная и непрерыв. в А, имеет локальный экстремум в т.х0А, если такая -окрестность х0, что для х (х0-, х0+) выполн.усл-е знакопостоянства приращения f (f≥0 или f≤0).В первом случае f(x)>f(x0) при х≠х0 и f(х0) нзв лок.минимумом; во 2-ом случае f(x)<f(x0) при х≠х0 и f(х0) нзв лок.максимумом. Справедливо, если f(x) сохраняет непрерывность в т.х0. Необх.усл-е экс-ма: Если в т.х0: 1) имеется лок. экс-мум; 2)существ.производная, то в этой точке она обращается в 0. Док-во: пусть х0 – т.лок.макс-ма.=> f≤0 при х(-,). Т.к.в точке существ.производная, то существ.оба одностор.предела и они равны.
1) при x>0 f/x≤0
2)
при x<0 f/x≥0
т.е. f’ должно быть ≤0 и ≥0 одновременно, что возможно только в случае f’(x0)=0. Замечание: в т.лок.экс-ма производная может не существовать (как конеч.число).
|
24. Достаточное усл-е экстремума ф-ии. Пусть f’(x) определена в проколотой окрест-ти точки х0, а сама ф-ия f(x) непрерывна в некотор.окрест-ти х0. Тогда, если f’(x) имеет разные знаки слева и справа от х0, то в т.х0 экстремум ф-ии. Док-во: проверим, что в усл-ях теоремы f имеет пост.знак при х(-,) f(x) имеет знак а (+ или -) и сменила знак на ā (- или +).
Рассмотрим знак величины f. f=f(x0+x)-f(x0)=(по теореме Лагранжа) f’(c)*x
Знак f не зависит от знака х, т.е. в т.х0 есть экстремум.
25. Асимптоты графика ф-ии. Асимптотой кривой нзв прямая, к к-рой неограниченно приближается точка кривой при ее удалении по кривой в бесконечность. I. Если lim f(x) = , то прямая х=а нзв вертикальной xa асимптотой. Напр. y=lnx lim lnx= - => x=0 вертик.ас-та x0+ Если ф-ия непрерывна в точке, то вертик.ас-тот нет. II. Если ф-ия f(x) представлена в виде f(x)=kx+b+α(x), где α(x) беск.малая при х+(-), у=kx+b нзв 1)горизонт.ас-той, если k=0; 2)наклон.ас-той, если k≠0. 1. Вычисление k:
2. Вычисление b: f(x)-kx=b+α(x) lim(f(x)-kx)=b x Замечание3: правило Лопиталя можно применять к неопред-тям вида 0, -, 1, 0, 00 , если предварительно выражение, от к-рого ищется предел, преобразовать.
26. Дифференциал и его геометрический смысл. Формула дифф-ла. Ф-ия нзв дифференцируемой в т.х0, если приращение ф-ии в этой точке может быть представлено в виде f=Ax+α(x)x, где А – постоянная, не завис.от x, α(x) – беск.малая при x0. Величина Ax явл.главным членом разложения у и нзв дифференциалом ф-ии f(x): df= Ax.
Геометр.смысл:
BC=AC*tgα=x*f’(x0)=df(x) f=DC; df=BC (дифф-ал f(x)– это приращение касательной к грфику в т.х0) f≈df. (*) Приближенное вычисление с помощью диф-ла основано на (*). Необходимо обратить внимание на ошибку вычисления или погрешность данной формулы. Оценка погрешности: - погрешность ≤max f″(x)(x)² x[x0; x0+x]
27. Функция от
нескольких переменных. Всякая
функция от нескольких переменных
становится функциейот меньшего числа
переменных,если часть переменных
зафиксировать,т.е. придать постоянные
значения. Геометрическим изображением
(графиком) функции двух переменных z
= f
(x,y)
является, вообще говоря, поверхность
в пространстве Oxyz.
В некоторых случаях можно получить
наглядное геометрическое представление
о характере изменения функции,
рассматривая её линии уровня (или
поверхности уровня),т.е. линии (или
поверхности), где данная функция
сохраняет постоянное значение. Линией
уровня функции z=
f
( x,y)
называется множество всех точек
плоскости Oxy,
для которых данная функция имеет одно
и то же значение (изокривая). Поверхностью
уровня функции u=f
(x,y,z)
называется множество всех точек
пространства Oxyz,
для которых данная функция имеет одно
и то же значение (изоповерхности).
Полное
приращение,приращение, приобретаемое
функцией нескольких переменных, когда
все аргументы получают (вообще говоря,
не нулевые) приращения Dx1,
Dx2,...,
Dxn.
При некоторых условиях (например, если
все частные производные непрерывны)
П. п. можно представить в виде суммы
слагаемого, линейно зависящего от
приращений аргументов и называемого
полным
дифференциалом,
и слагаемого, бесконечно малого по
сравнению с
|
28. Частные приращения ф-ции и част.производные. Геом.смысл част.производных. Частная производная. Переменная z называется однозначной функцией переменных x и y, если каждой паре значений x и y в некоторой области из изменения постановлено в соответствие одно значение z.Функционально зависимость z от x и y записывают в виде z=F(x.y)
Производная
функции z=F(x,y)
по x
,найденная в предположении, что y
остается постоянным называют частной
производной
z
по x
и обозначается
Геом. смысл: уравнение z=F(x.y) геометрически определяет некоторую поверхность. Пара значений x и y определяет на плоскости xOy точку P(x,y) , а z=F(x,y) - аппликату соответствующей точки M(x,y,z) на поверхности. Поэтому говорят, что есть функция точки P(x,y) , и пишут z=F(P)
29. Частные производные высших порядков.
Пусть дана функция,
имеющая частные производные
Аналогично, определяются и обозначаются частные производные третьего порядка:
Для вычисления част.производных справедливы все правила, выведенные для ф-ций одной переменной. Теорема о смешанных производных: если смеш.част.производные непрерывны в некотор.точке, то они равны между собой в этой точке. 30. Полный дифференциал функций многих переменных. Методы дифференциальных исчислений применяются для изучения функций нескольких переменных. Для функции двух независимых переменных z = f (х, у) частной производной по х называется производная этой функции по х при постоянном у. Эта частная производная обозначается z'x, f'x (x, y), ¶z/¶х или ¶f (x, y)/¶x, так что
Аналогично определяется и обозначается частная производная z по у. Величина Dz = f (x + Dx, y + Dy) - f (x, y) называется полным приращением функции z = f (x, y). Если его можно представить в виде Dz = ADx + ВDу + a, где a — бесконечно малая более высокого порядка, чем расстояние между точками (х, у) и (х + Dх, у + Dу), то говорят, что функция z = f (x, y) дифференцируема. Слагаемые АDх + ВDу образуют полный дифференциал dz функции z = f (x, y), причём А = z'x, B = z'y. Вместо Dx и Dy обычно пишут dx и dy, так что
Геометрически дифференцируемость функции двух переменных означает существование у её графика касательной плоскости, а дифференциал представляет собой приращение аппликаты касательной плоскости, когда независимые переменные получают приращения dx и dy. Для функции двух переменных понятие дифференциала является значительно более важным и естественным, чем понятие частных производных. В отличие от функций одного переменного, для функций двух переменных существование обеих частных производных первого порядка ещё не гарантирует дифференцируемости функции. Однако, если частные производные кроме того ещё непрерывны, то функция дифференцируема. Аналогично определяются частные производные высших порядков. Частные производные ¶2f/¶х2 и ¶2f/¶у2, в которых дифференцирование ведётся по одному переменному, называют чистыми, а частные производные ¶2f/¶x¶y и ¶2f/¶у¶х— смешанными. Если смешанные частные производные непрерывны, то они между собой равны. Все эти определения и обозначения переносятся на случай большего числа переменных.
31. Необходимое условие экстремума ф-ции 2-х переменных. Точки возможного экстремума и стационарные точки. Точка локал.min: (х0,у0) явл.точкой локал.мин f(x,y), если f(x,y)≥ f(x0,y0) при (x,y)U(M0). Аналогично относительно точки локал.макс. Общее название точек мин. и макс. – экстремумы.
Если функция
имеет экстремум в некоторой точке, и
в этой точке определены обе частные
производные, то они обязаны обратиться
в ноль. Эти точки называются критическими. 32. Достаточное условие экстремума ф-ции 2-х переменных. Примеры критических точек и наличие или отсутствие экстремума в них.
Пусть
а)
если
б)
в)
|
33. Условный экстремум 1) Усл-ый экстремум (метод множ-ей Лагранжа): Постановка задачи: Найти экстремумы ф-ии Z=f(x,y) при усл, что φ(x,y)=0. Составляют ф-ию Лагранжа: L=f(x,y) + η φ(x,y) ; η – множ-ль Лагранжа. Для того, чтобы найти т экстремума, находят стац-е точки ф-ии Лагранжа, т.е. решают систему:
Достат-ое усл экстремума: Если опред-ль ∆>0, то экстр-м есть и при том max; Если ∆<0 => экст-м есть – min
вычисленный в точке (x0, y0, λ 0) (стац т). 34. Метод наименьших квадратов. (x1; y1) (x2; y2) (xn; yn)
Подобрать теоретич. прямую вида y=ax+b "наилучшим образом" согласующуюся с этими данными. δi=yi теор – yi эмпирич; МНК:∑(δi)2→min
35. Первообразная.ее св-ва Если F΄(х)=f(х), х€J,тогда F(х)-первообразная для ф-ции f(х), 1.пусть F(х) первообр. f(х), х€J,G(х)-первообр.g(х), х€J, к-число, тогда а) F(х)+ G(х) первообр для f(х)+ g(х), х€J б) к ∙F(х)-первооб для к ∙ f(х) 2.а) F(х)+С является первообр для f(х) для всех С. б)если F1 другая первообразн для f(х), то существует число С, для к-рого F1(х)= F(х)+С Неопределенный интеграл и его св-ва. Неопред. интегралом от функции f(x) на данном промежутке наз. множество всех первообразных от этой ф-ии на этом промежутке.
Св-ва неопредел. интеграла. Интегр-ие – действие, обратное диффер-ию. 1) (∫f(x)dx)' = f(x); 2) d (∫f(x)dx)=f(x)dx; 3)∫df(x)= f(x)+c 4)∫f ' (x)dx = f(x)+c 36. Метод интегр-ия по частям и рекомендации. ∫udv = uv – ∫vdu. Док-во: d(uv)=duv + udv ; d(uv) – duv=udv ; ∫udv=uv – ∫vdu. Метод применяется, когда подинтегр. ф-ия предст-ет собой произведение алгебр-ой и трансцендентной ф-ий. При этом за ф-ию u принимают ту часть подинт-го выр-ия, к-ая упрощается при дифф-ии, а к dv – часть, интеграл от к-ой может быть вычислен. Обратные и трансцинд-ые ф-ии обычно относят к u (лог-ие и обратно тригоном-ие). 1) ∫ многочлен ∙ тригоном показат dx └─────┘ └────────────┘ u dv 2) ∫ обрат трансц ∙ многочлен dx └──────┘ └────────┘
37. Метод замены переменных. Вывод ф-лы. Примеры. Пусть F(x) первообр для f(x); x=φ(t)
Надо проверить, что ф-ия F(φ(t)) явл первообр для подинтегр ф-ии f(φ(t))* φ’(t)dt
Следствие: Подстановку x= φ(t) можно осущ как до интегр, так и после – результаты будут одинаковы.
∫((ln3x)/x)dx=∫((ln3x)/x)* (d(lnx))/(lnx)'=∫u3du=(ln4x)/4 +c
u dv
38. Интегр-ие тригоном-их ф-ий. 1) Преобразование произв-ия в сумму. cosαx cosβx, sinαx sinβx, sinαx cosβx. cosαx ∙ cosβx = ½(cos(α−β)x + cos(α+β)x) sinαx∙ sinβx=½(cos(α−β)x – cos(α+β)x) sinαx∙ cosβx=½(sin(α−β)x + sin(α+β)x) 2) ∫sinmx cosnx dx a) среди m и n есть нечетное, значит от нечетной степ. отдел. 1 сомножитель и подводится под дифф-л.sin2x + cos2x=1 б) m и n - четные, тогда sin2x = (1-cos2x)/2, cos2x = (1+cos2x)/2 ; sinx cosx = (sin2x)/2. Универсальная подстановка.∫R(sinx, cosx)dx; tg(x/2)=t , => x=2arctg t , dx= (2/(1+t2)) dt , тогда sinx=(2/(1+t2)), cosx = (1-t2)/ (1+t2)
|
||||||||||||
|
39. Интегрирование нек-ых рациональных ф-ий. Отношение многоч-ов назыв рац-ой ф-ей. Если степень мног-на в числителе равна или больше степени мног-на в знаменателе, то рац-ая ф-ия назыв неправильной дробью, в противном случае-правильной. Из всякой прав-ой др можно выделить целую часть (мног-ен) и правильную др, для этого мног-ен числителя делят «уголком» на мног-ен знамен-ля. При делении мног-ов «уголком», старший одночлен делимого делится на старший одночлен делителя. Результат деления запис-ся в след виде:
Правильная др раскл-ся в сумму простейших др-ей. Имеется 4 типа правильных дробей:
Для того, чтобы выяснить, как выгл разложение в сумму прост-их, поступают след образом: знам-ль расклад в произв-е сомн-ей (x – a), x2+px+q, (p2-4q<0). Затем, если сомн-ль (x – a)k появ в степени k, то в разложении в сумму простейших возн-ет выр-ие:
A1, A2, Ak – это числа, кот-ые нужно найти.
40. Определенный интеграл. Ньютон-Лейбниц Определенный интеграл
Пусть
функция f(х) определена на отрезке
где
называется интегральной суммой функции f(x) на отрезке [а, b].
Предел
интегральной суммы Sn
при
условии, что число разбиений отрезка
[а,
b]
неограниченно увеличивается,
т.е.
где f(x) – подынтегральная функция; а – нижний предел интегрирования;
b
- верхний предел интегрирования.
Формулой
Ньютона - Лейбница называется равенство
вида:
|
41. Вычисление площадей плоских фигур с помощьюопределенного интеграла. Для вычисления площади плоской фигуры обычно используют следующие этапы: 1) определяется вид искомой площади фигуры 2)устанавливаются пределы интегрирования 3)устанавливаются участки, на которых подынтегральная функция положительная и отрицательная 4)берутся интегралы, на каждом участке находится суммарная абсолютная величина площадей этих участков Если требуется вычислить S фигуры, ограниченной двумя кривыми на участке [a,b] y1= f1(x), y2=f2(x), то искомая S находится как разность площадей криволинейных трапеций, ограниченных разными кривыми
S= a∫b f1(x)dx - a∫b f2(x)dx = a∫b (f1(x) - f2(x))dx В некоторых случаях пределы интегрирования не заданы,и они находятся в процессе решения.
42. Вычисление объёмов тел вращения. Проведем через х сечение, перпендикулярное Ох . S (x)=π y2 ∆xi=xi+1 - xi Si= π y2(xi) Vi=Si∆Xi Vn=i=0∑n=1 πy2(Xi)∆Xi = - интегральная сумма для б(х) = i=0∑n=1 S(Xi) )∆Xi Предел этой суммы – объём этой фигуры V=limn→∞ i=0∑n=1 б(Xi) ∆Xi = a∫b S(x)dx = π a∫b y2dx U= f a∫b x 2 dy
43. Вычисление длины кривой. Изобразим на плоскости Оху некоторую кривую y=f(x) на [a,b] Разобъём [a,b] на n в общем случае равных частей. Восстановим перпендикуляры, соединим точки А1,М1,М2 и т.д. хордой Мi Mi+1 ∆Yi=Yi+1 – Yi ∆Si= √(∆Xi^2 + ∆Yi^2) = √( 1 + ∆Yi^2 / ∆ Xi^2) ∆Xi
Sn= i=0∑n=1 ∆Si= i=0∑n=1 √(1 + ∆Yi^2 / ∆ Xi^2) ∆Xi
Применим формулу Лагранжа для приращения функции f’(Xi)= ∆Yi / ∆Xi Sn= i=0∑n=1 √(1 + f ’ ^2 (Xi)) ∆Xi S= a∫b √(1 + f ’ ^2 (X))dx = a∫b √(1 + Y ^2(x)) dx
44. Приближенное вычисление определенного интеграла а). Метод трапеций. Пусть необходимо вычислить
который вычисляется точно далеко не всегда. Воспользуемся геометрическим смыслом и получим приближенную формулу для вычисления интеграла.
Рис. 4.3
Разобьем отрезок
[a,b]
на n равных частей длиной
Тогда точки разбиения хi = х0+i×h, a yi = f(xi), i = 0,1, ... , n дадут нам n трапеций с основаниями yi = f(xi) и высотой h. Суммируя площади этих трапеций, будем иметь формулу трапеций для вычисления приближенного интеграла
|
45. несобственные интегралы 1-го и 2-го рода Несобственные интегралы 1-го рода – это несобственные интегралы с бесконечными пределами. a∫+∞f(x)dx =limb→+∞ a∫bf(x)dx, если этот предел существует и равен конечному числу, то это число и есть значение несобственного интеграла; если же этот предел не существует или равен бесконечности, то говорят,что несобственный интеграл расходится.
Несобственные интегралы 2-го рода – этонесобственные интегралы от неограниченной ф-ции.Выделяют 4 разновидности несобственных интегралов 2-го рода:
a∫bf(x)dx=limε→ο+ a+ε∫bf(x)dx 2)когда f(x) неогранич в левосторон окрестн x=b a∫bf(x)dx= limε→ο+ a∫b-εf(x)dx 3)когда f(x) неогранич в любой двусторон окрестности x=c € (a;b) a∫bf(x)dx= a∫cf(x)dx+ c∫bf(x)dx, оба интеграла должны в сумме сходится в число, если же хотя бы один из интегралов в сумме расходится, то интеграл по отрезку [а;b] тоже расходится 4) когда f(x) неограниченна в x=a и в x=b a∫bf(x)dx= a∫cf(x)dx+ c∫bf(x)dx, если оба интеграла в сумме сходятся, то интеграл подсчитывается. 46. Кратный интеграл,интеграл от функции, заданной в какой-либо области на плоскости, в трёхмерном или n-мерном пространстве. Среди К. и. различают двойные интегралы, тройные интегралы и т. д. n-кратные интегралы.
Пусть
функция f
(x,
y)
задана в некоторой области D
плоскости хОу.
Разобьем область D
на n
частичных областей di,
площади
которых равны si,
выберем в каждой области di
точку (xi,
hi)
(см.
рис.)
и составим интегральную сумму
|
|

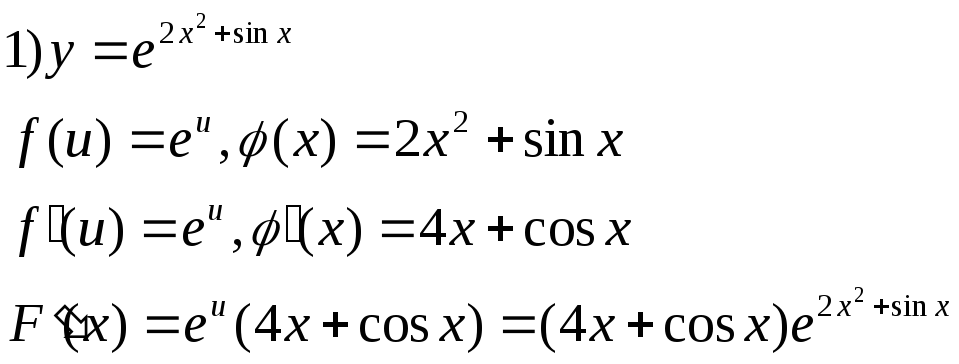
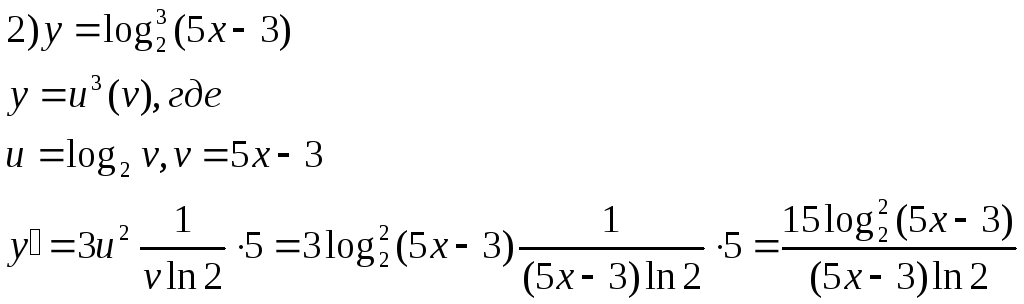


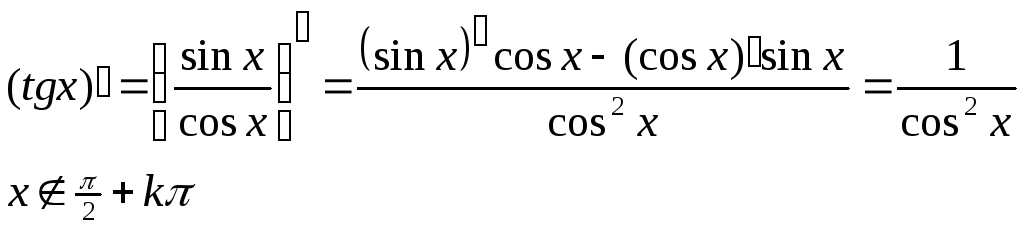
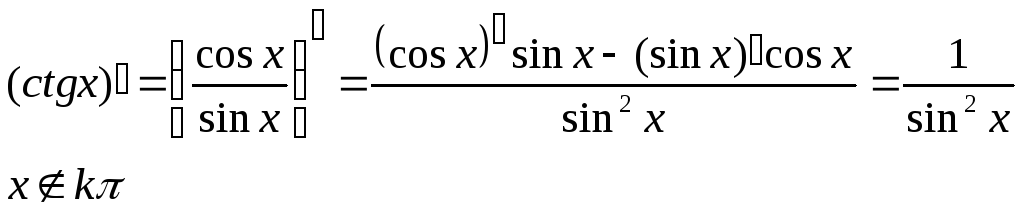
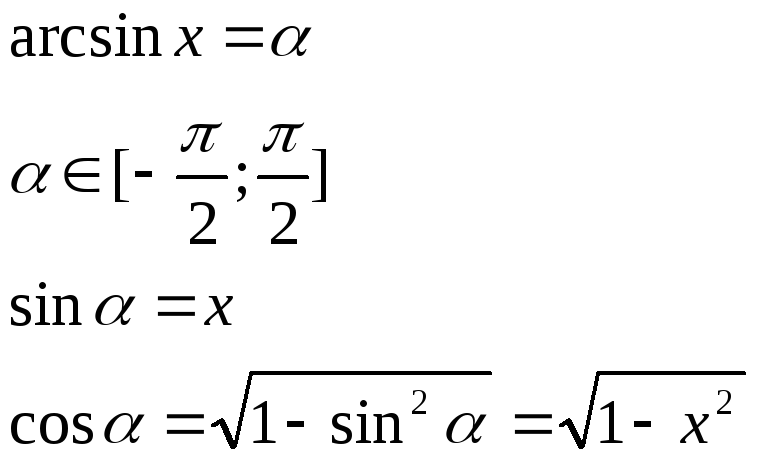

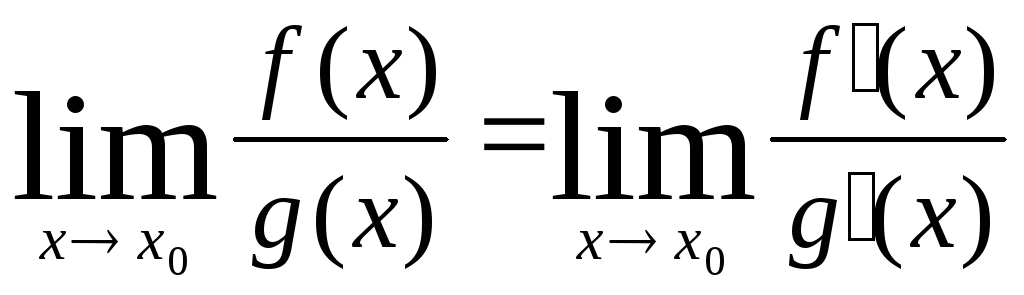

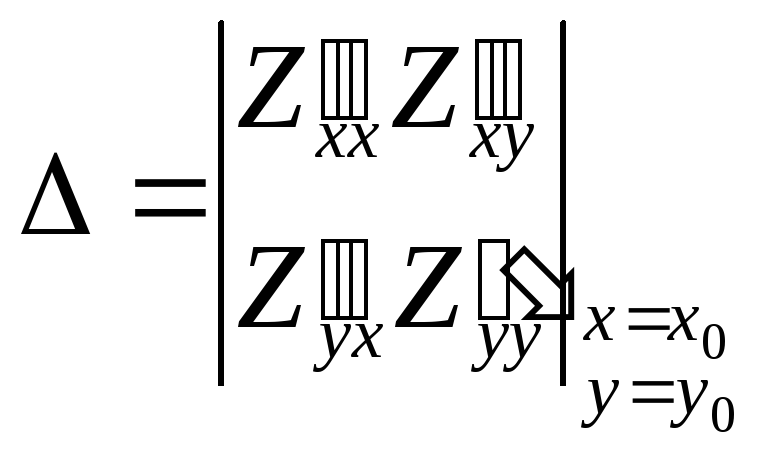
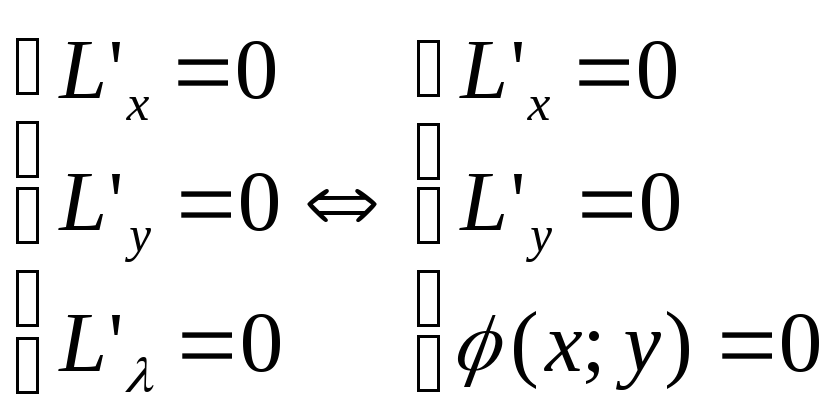

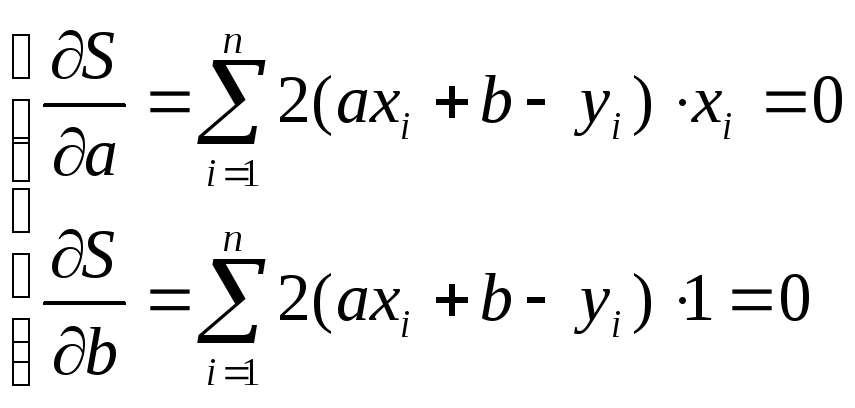


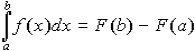 При
этом предполагается, что подынтегральная
функция f(x)
непрерывна при всех значениях x,
удовлетворяющих условиям a
x
b.
При
этом предполагается, что подынтегральная
функция f(x)
непрерывна при всех значениях x,
удовлетворяющих условиям a
x
b.