
7-Применение определителей к системе линейных уравнений.
Рассмотрим кв.систему линейных ур-ний:
а 11х1+а12х2+…+а1nxn=b1
(1)
11х1+а12х2+…+а1nxn=b1
(1)
an1x1+an2x2+…+annxn=bn
d
 et
A=а11
а12
а1n
et
A=а11
а12
а1n
an1 an2 ann
Теорема 1 (Крамера)
пусть кв. система лин. ур-ний (1) имеет отличный от нуля определитель D (D≠0), тогда сист.(1) является определенной – имеет единственное решение (k1, k2, …, kn) и решение находится по формуле kj=Dj/D . Dj – определитель, получаемый из определителя D заменой его j-столбца на столбец свободных членов сист.(1).
Теорема 2.
Если система n-линейных однородных уравнений с n неизвестными имеет ненулевые решения, то определитель системы D=0.
Доказательство:
Тк столбец свободных членов нулевой, то D1=D2=…=Dn=0, тк каждый такой определитель создает нулевой столбец kj=Dj/D. Если D≠0, то тогда решение (k1, k2, …, kn)=(0,0,…,0), по т.1(Крамера) решение единственное. Если D=0, система неопределенная и кроме тривиальных решений сущ. ненулевые решения. Система дает необх.условие существования ненулевых решений. D=0 кв.система однород.ур-ний имеет ненулевые решения.
18. Доказать теорему: базис системы векторов есть максимальная линейно независимая часть этой системы.
Пусть ai1, ai2, …, air – базис сист.векторов a1, a2,…,an.
Добавим любой aj из данной системы. Получим ai1, ai2, …, air, aj. По определению базиса, любой вектор данной сист.векторов разлагается по базису: aj=k1ai1+k2ai2+…+krair. По теореме 2 (сист.векторов явл.л.з. óесли хотя бы 1 из них явл.лин.комбинацией остальных векторов)=> ai1, ai2, …, air, aj – лин.з.=> ai1, ai2, …, air – max л.н.часть.
Билет 10.
Пусть квадр.матрица
порядка n-
это А.Квадратн.матрица
назыв.неособенной(невырожденной),если
ее определитель не равен нулю.Если ее
определитель равен нулю,то она
особенная(вырожденная).Если существует
матрица В,такая что АВ=ВА=Е,то В
назыв.обратной матр.А(В=![]() ).
).
Теорема:Если матрица невырожденная,то она имеет обратную матрицу и при том единственную.
Д-во: Пусть А=![]() – квадратная. DetA≠0-невырожденный,составим
à =
– квадратная. DetA≠0-невырожденный,составим
à = ![]() ,где
,где ![]() -алгебраическое
дополнение элементов
-алгебраическое
дополнение элементов ![]() в определителе А. det
в определителе А. det![]() =1,n.Подчеркнём,что
в i-ой строке матрицы Ã стоят
алгебраич.дополнения к элементам i-ого
столбца DetA.Матрицу
à наз.присоединенной матрицей А.Умножим
все элементы Ã на число
=1,n.Подчеркнём,что
в i-ой строке матрицы Ã стоят
алгебраич.дополнения к элементам i-ого
столбца DetA.Матрицу
à наз.присоединенной матрицей А.Умножим
все элементы Ã на число ![]() =
=![]()
![]() =
=![]()
Докажем,что матрица
![]() обратная матрица.Составим произв-е
обратная матрица.Составим произв-е
![]() *
А
*
А
![]() =
=
![]() *
* 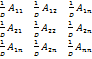 =
= 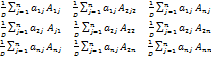
По свойству 3
определителя суммы расположен на главной
диагонали ![]() *
А есть DetA=D
по св-ву 5 определителя,все остальные
суммы равны нулю.
*
А есть DetA=D
по св-ву 5 определителя,все остальные
суммы равны нулю.
А*![]() =
=
![]() = Е. Докажем сущ-е
= Е. Докажем сущ-е ![]() :Докажем
единственность
:Докажем
единственность ![]() .Предположим
сущ-е еще матр.ЕС,такая что АС=СА=Е.
.Предположим
сущ-е еще матр.ЕС,такая что АС=СА=Е.
![]() *
АС=
*
АС=![]() *А*С=ЕС=С
;
*А*С=ЕС=С
; ![]() *
АС=
*
АС=![]() след. С=
след. С=![]()
Билет 26.
![]() +
+![]() +…+
+…+![]() - однородная система ур-й (1). АХ=
- однородная система ур-й (1). АХ=![]() ,(2)
,(2)
![]() -матрица
коэф-ов системы ; Х-столбец неизвестности
-матрица
коэф-ов системы ; Х-столбец неизвестности
Свойства:1. Если
![]() -решение
(2), то λ
-решение
(2), то λ![]() ,
где λ-число,тоже решение однородн.сис-мы.
2.Если
,
где λ-число,тоже решение однородн.сис-мы.
2.Если ![]() -решение(2),то
(
-решение(2),то
(![]() )-решение(2).
3.Если
)-решение(2).
3.Если ![]() …
…![]() -решение(2),то
их линейная комбинация
-решение(2),то
их линейная комбинация ![]() +…+
+…+![]() -решение(2).
-решение(2).
Применяя теорему(совместная система будет неопределенной,если ранг сис-мы ур-й меньше,чем число неизвестных)к однородн.системе ур-й.Сделаем след.выводы: если r(A)=n,то (2) имеет единств.тривиальное решение. 2)если r(A)<n,то (2) явл. Неопредел.,т.е иметт нетривиал.реш-я.Мы знаем,что всякая сис-ма n-мерных векторов,включ. Более n-векторов будет л.-з. Решениями(2)явл. n-мерные векторы.Поэтому из них можно выбрать конечную максим. Л-н.систему,т.е. такую,что любое решение(2) будет л.комбинацией этих выбран.векторов. Всякая максим.лин-незав.система решений однор.сис-мы ур-ий назыв.её ФСР.Условие сущ-я ФСР устанавливает след.теорема: Если r(A)<n, то ФСР однор.сис-мы(2) суш-ет и состоит из n решений.
№29. Собственные вектора и собственные значения лин-го преобр-я, их отыскание
Ненулевой вектор х(с чертой наверху, далее просто черта) назыв-ся собственным вектором л.п. α (альфа), если оно переводит х(ч) в коллинеарный ему λх(черта):
α (х(черта))= λх(черта) (1)
Число λ в (1) наз-ся собственным значением преобразования α (альфа), соответствующим собственному вектору х(черта). Найдем все собственные векторы:
Пусть:
е1(четра), е2(четра),…, еn(четра) – базис Rn
Система (фигурные скобки): (2)
λх1=a11x1+a12x2+…+a1nxn,
λх2= a21x1+a22x2+…+a2nxn,
…
λхn= an1x1+an2x2+…+annxn .
Система (3):
(a11-λ)x1+a12x2+…+a1nxn=0,
a21x1+(a22-λ)x2+…+a2nxn=0,
…
an1x1+an2x2+…+(ann-λ)xn=0.
Однородная система (3) имеет ненулевые решения тогда и только тогда, когда ее определитель = 0.
Определитель (прямые скобки): (4)
a11-λ a12 … a1n
a21 a22-λ … a2n = 0
…
an1 … ann-λ
Многочлен n-ой степени относительно λ в левой части уравнения (4) – характеристический многочлен преобразования α (альфа).
Уравнение (4) – характеристическое уравнение преобразования α (альфа).
Всякому действительному корню λ 0 ур-я (4) отвечает собственный вектор, который находится путем реш-я совместной системы (3) относительно x1,x2,…,xn после подстановки λ 0 вместо λ в эту систему.
Замечание:
В матричной форме система (3):
(A- λE)X=θ , где
A - матрица лин. преобр-я α (альфа),
Е – единичная матрица того же порядка, что и А,
Х – вектор-столбец из координат вектора х(черта).
Отыскание:
1)множество собственных значений лин. преобр-я α (х(черта)):
det(A- λE)=0 – характеристическое уравнение
2)Собственные векторы:
(A- λiE)X=θ
Вопрос 9. Матричная форма записи системы линейных уравнений.
Пусть дана система m линейных уравнений с n неизвестными:
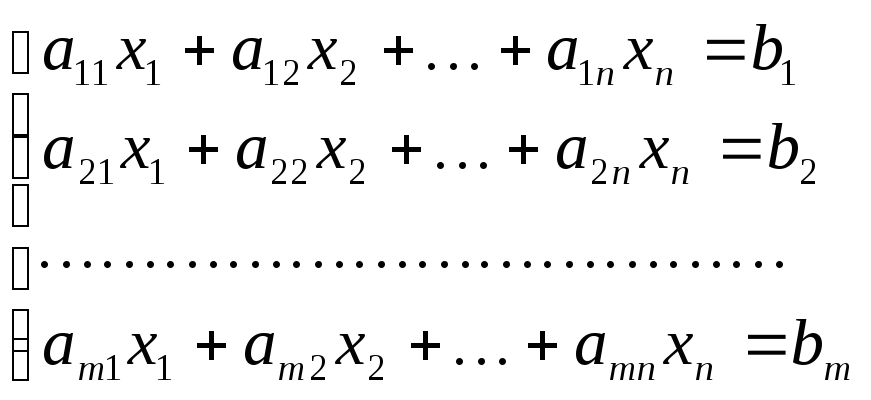 (1)
(1)
Выпишем матрицу, составленную из коэффициентов при неизвестных в системе (1)
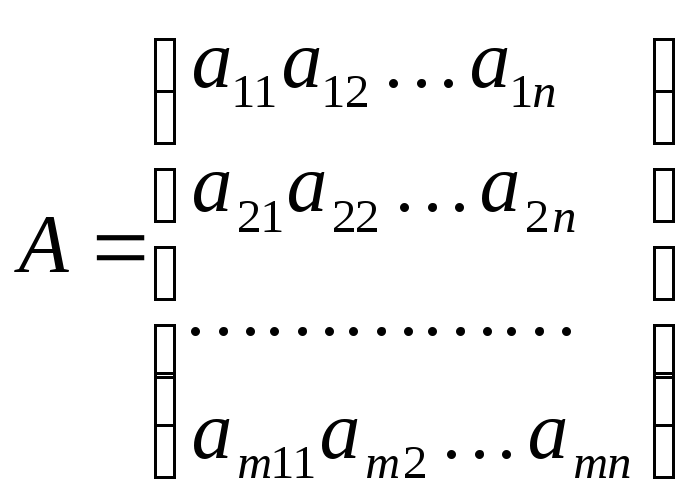 -
матрица системы (1)
-
матрица системы (1)
 -
матрица-столбец из неизвестных системы
(1)
-
матрица-столбец из неизвестных системы
(1)
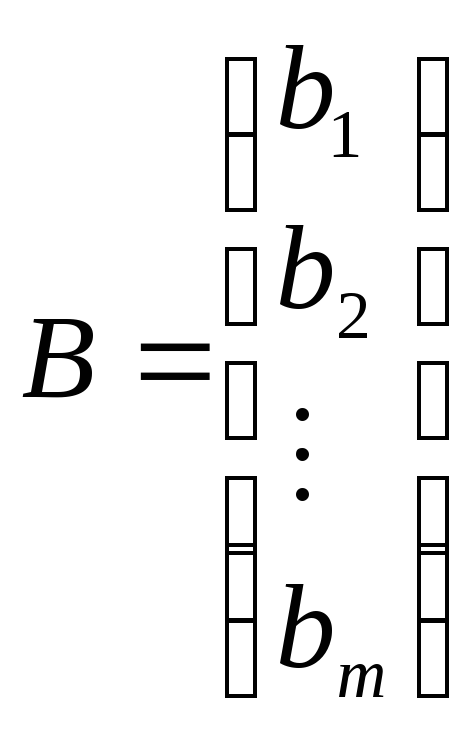 -
матрица-столбец из свободных членов
системы (1)
-
матрица-столбец из свободных членов
системы (1)
AX – существует
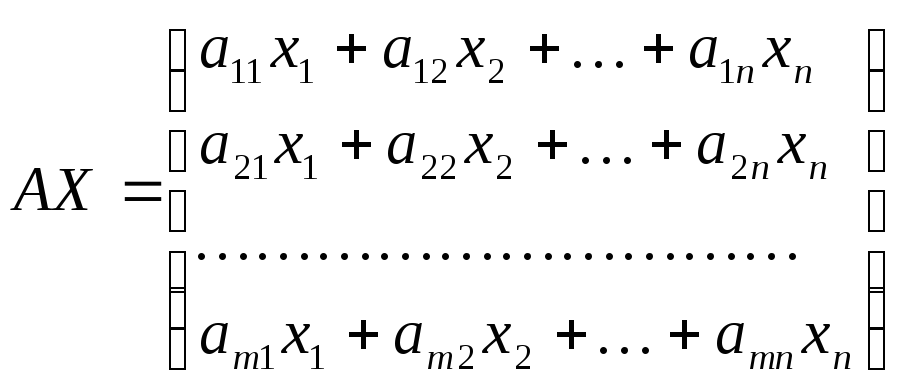
АХ имеет m строк и 1 столбец, - это матрица-столбец, элементы которого являются левые части уравнения (1)
АХ=В – матричная форма записи системы линейных уравнений
19 билет. Доказать теорему: каждую линейно независимую часть системы векторов а1, а2…аs можно дополнить до базиса этой системы.
Если данные лин-независимые части не явл-ся базисом данной системы векторов, то она не максимальна, и к ней можно добавить 1 вектор из сис-мы а1, а2, … an так, что полученная новая часть ai1, ai2, … ais, ais+1 – Лин. Нез.
Если эта новая часть все еще не максимальна, то к ней можно добавить еще один вектор и т.д.
Процесс расширения Лин. Нез. части после добавления очередного вектора должен закончиться, т.к. к ЛН части а1…аs сис-мы векторов а1,а2…аn можно добавлять не более (n-s) векторов.
Следствие. Если в сис-ме векторов есть ненулевой вектор, то она меняет базис.
Док-во. Сис-ма, состоящая из 1 ненулевого вектора, - ЛН: а1 ≠ Ө, k1а1=Ө k1=0 => сис-ма из одного ненулевого вектора ЛН => тогда, по осн. теореме 3, ЛН часть системы, состоящую из одного ненулевого вектора можно дополнить до базиса этой сис-мы.
№3 Исследование и решение систем линейных уравнений методом Ж- Гаусса.
Сущность метода Ж- Гаусса заключается в том, что при нахождении конечного числа элементарных преобразований система линейных уравнений преобразуется в эквивалентную- т.е разрешённую систему уравнений или эквивалентную ей несовместную систему. Процесс решений состоит из ряда последовательных этапов расчетов. После выполнения каждого этапа, система линейных уравнений становится разрешаемой относительно какого-либо неизвестного.
Процесс преобразований закончится в след. 2-х случаях:
1)мы придём к системе уравнений, содержащих уравнение вида 0=b, b≠0,тем самым установим несовместность исходной системы(1.2)
2)получим разрешённую систему уравнений ,эквивалентную системе (1.2) , очевидно число уравнений (r) в разрешенной системе ≤m-числа уравнений в системе (1.2) т.к в процессе преобразования мы отбросили уравнение 0=0…..r<n
r-число уравнений в разрешённой системе…. n-число неизвестных
*r=n
т.е. система
совместная и определённая,
система уравнений имеет вид ![]() (1.13)
(1.13)
Система
(1.13) и равносильная ей (1.2) имеют единственное
решение(![]() ,
,
![]() ,
,![]() )-
совместная; определённая
)-
совместная; определённая
*r<n
разрешённая система имеет вид ![]() (1.14)
(1.14)
В
системе (1,14) неизвестные (![]() ,
,![]() )
составляют набор разрешённых
неизвестных,
а остальные неизвестные- называются
свободными
неизвестными.
)
составляют набор разрешённых
неизвестных,
а остальные неизвестные- называются
свободными
неизвестными.
Возьмём
для свободных неизвестных произвольные
числовые значения ![]() подставим их в систему (1.14) вместо
соответствующих неизвестных, найдём
значение для разрешённых (базисных)
неизвестных
подставим их в систему (1.14) вместо
соответствующих неизвестных, найдём
значение для разрешённых (базисных)
неизвестных ![]() -
-![]()
![]() -
-![]()
![]() -
-![]()
Легко
проверить, что набор чисел (![]()
![]() является решением системы (1.14) →равносильной
ей системы (1,2) т к свободным неизвестным
можно передавать произвольное числовое
значение, то таким образом можно найти
бесконечное множество решений системы
(1,2), в случае r<n
система (1.2) является совместной,
но неопределённой.
является решением системы (1.14) →равносильной
ей системы (1,2) т к свободным неизвестным
можно передавать произвольное числовое
значение, то таким образом можно найти
бесконечное множество решений системы
(1,2), в случае r<n
система (1.2) является совместной,
но неопределённой.
Каждое
решение такой системы называется её
частным решением, выраженным в базисных
и неизвестных через свободные т.е.
![]() =
=![]() -..-
-..-![]()
![]() =
=![]() -...-
-...-![]() (1.15)
(1.15)
![]() -..-
-..-![]()
Называется общим решением системы (1,2) и (1,14) среди частных решений. Выделим базисные, которые получаются при нулевых значениях всех свободных неизвестных.
Базисное
решение ![]()
Из всего сказанного можно сделать выводы: система линейных уравнений будет несовместной, если при выполнении этапов преобразования по методу Ж- Гаусса мы получим противоречивое уравнение, если же такого уравнения нет, то система будет совместной.
Совместная система будет определённой, если она приводится к разрешённой системе в которой число уравнений равно числу неизвестных. И неопределённой, если в разрешённой системе число уравнений меньше числа неизвестных.
Следствие1! Если m<n, то система уравнений либо несовместная, либо неопределённая
Доказательство: Если система уравнений (1,2) является совместной, то она является определённой или неопределённой, это зависит от числа разрешённых в уравнении.
r≤ m ≤n, то система (1,2)- неопределённая .
Замечание1.Рассмотрим
систему линейных уравнений, в которой
свободные члены всех уравнений=0
![]() i=1,m
(1.16)
i=1,m
(1.16)
J=1
Такая система (1.16) называется системой линейных однородных уравнений. Эта система всегда совместна т к имеет тривиальное (нулевое) решение.
Для системы (1,16) вопрос стоит в том, определённая она или не определённая. Система (1,16) является определённой, если она имеет только тривиальное решение и неопределённая, если кроме тривиального есть не нулевые.
Следствие2! Если m<n то система помимо нулевого имеет и ненулевое решение.
Замечание2
чтобы
записать систему (1,2) нужно знать
коэффициенты уравнений и свободные
члены. Выписываем их в виде таблицы.
![]()
Получим таблицу из чисел, которая содержит m строк и n+1 столбцы. Всякая прямоугольная таблица из чисел называется МАТРИЦЕЙ. Числа, составляющие матрицу,- её Элементы.
Элементы
одного n
столбца имеют 2 индекса. ![]()
![]()
![]()
Матрица
![]() является расширенной матрицей системы
(1,2) она получается путём присоединения
к матрице из коэффициентов сист (1,2)
столбца свободных членов.
является расширенной матрицей системы
(1,2) она получается путём присоединения
к матрице из коэффициентов сист (1,2)
столбца свободных членов.
Билет 25. Теорема: любая совокупность значений свободных неизвестных определяет однозначно решение системы линейных уравнений
Пусть дана сис-ма
ур-й ![]() 1x1+
1x1+![]() 2x2+…+
2x2+…+![]() nxn
=
nxn
= ![]() (1)
(1)
Док-во.
Пусть ![]() 1,
1,
![]() 2…
2…![]() r
образуют базис системы векторов –
коэффициентов. Ранг сис-мы равен n,
остальные неизвестные будут свободными.
r
образуют базис системы векторов –
коэффициентов. Ранг сис-мы равен n,
остальные неизвестные будут свободными.
![]() 1х1+...+
1х1+...+![]() rхr
=
rхr
= ![]() -
- ![]() r+1xr+1
- … -
r+1xr+1
- … - ![]() nxn
(2)
nxn
(2)
Зададим свободным
неизвестным любые значения: xr+1=kr+1,
xr+2=kr+2,
… , xn=kn
. Подставим
эти значения в правую часть (2) вместо
неизвестных: ![]() =
= ![]() –
– ![]() r+1kr+1
- … -
r+1kr+1
- … - ![]() nkn
nkn
Перепишем рав-во
(2) в виде: ![]() 1x1+…+
1x1+…+
![]() rxr
=
rxr
= ![]() (3)
(3)
Рав-во (3) можно
рассматривать как разложение вектора
![]() по векторам базиса, коэффициенты кот.
x1=k1,
… , xr=kr
есть значения
базисных неизвестных. Числа k1,
k2…
kr
– значения базисных неизвестных,
определяются однозначно => однозначно
определяется решение системы уравнений
(1):
по векторам базиса, коэффициенты кот.
x1=k1,
… , xr=kr
есть значения
базисных неизвестных. Числа k1,
k2…
kr
– значения базисных неизвестных,
определяются однозначно => однозначно
определяется решение системы уравнений
(1): ![]() = (k1,
k2,
… , kr+1,
… kn)
= (k1,
k2,
… , kr+1,
… kn)
Решение, кот.
появляется при нулевых значениях ![]() =(
=(
![]() 1,
1,
![]() 2,
… ,
2,
… , ![]() r,
0 … 0) называется базисным решением.
r,
0 … 0) называется базисным решением.
19 билет. Доказать
теорему:
каждую линейно независимую часть системы
векторов ![]() 1,
1,
![]() 2…
2…![]() s
можно дополнить до базиса этой системы.
s
можно дополнить до базиса этой системы.
Если данные
лин-независимые части не явл-ся базисом
данной системы векторов, то она не
максимальна, и к ней можно добавить 1
вектор из сис-мы ![]() 1,
1,
![]() 2,
…
2,
… ![]() n
так, что
полученная новая часть
n
так, что
полученная новая часть ![]() i1,
i1,
![]() i2,
…
i2,
… ![]() is,
is,
![]() is+1
– Лин. Нез.
is+1
– Лин. Нез.
Если эта новая часть все еще не максимальна, то к ней можно добавить еще один вектор и т.д.
Процесс расширения
Лин. Нез. части после добавления очередного
вектора должен закончиться, т.к. к ЛН
части ![]() 1…
1…![]() s
сис-мы
векторов
s
сис-мы
векторов ![]() 1,
1,![]() 2…
2…![]() n
можно
добавлять не более (n-s)
векторов.
n
можно
добавлять не более (n-s)
векторов.
Следствие. Если в сис-ме векторов есть ненулевой вектор, то она меняет базис.
Док-во.
Сис-ма, состоящая из 1 ненулевого вектора,
- ЛН: ![]() 1
≠ Ө,
k1
1
≠ Ө,
k1![]() 1=Ө
k1=0
=> сис-ма из одного ненулевого вектора
ЛН => тогда, по осн. теореме 3, ЛН часть
системы, состоящую из одного ненулевого
вектора можно дополнить до базиса этой
сис-мы.
1=Ө
k1=0
=> сис-ма из одного ненулевого вектора
ЛН => тогда, по осн. теореме 3, ЛН часть
системы, состоящую из одного ненулевого
вектора можно дополнить до базиса этой
сис-мы.
Билет №1
![]() (1)
(1)
(а) 2 уравнения системы (1) меняются местами
(б) одно уравнение
системы (1) умножается на число
![]() ,
отличное от нуля
,
отличное от нуля
(в) к уравнению
системы (1) прибавляется другое уравнение,
умноженное на на число
![]()
Теорема об элементарных преобразованиях системы линейных уравнений
При любом элементарном преобразовании системы лин. уравнений получается система уравнений, эквивалентная данной
Доказательство:
очевидно, что при преобразовании (а) получается система, эквивалентная данной
выполним преобразование
(б). i-тое
уравнение системы (1) умножить на число
![]() ,
отличное от нуля.
,
отличное от нуля.
![]() - i-тое
уравнение системы(2), все остальные
уравнения, как в (1)
- i-тое
уравнение системы(2), все остальные
уравнения, как в (1)
Пусть
![]() ,
,![]() ,…,
,…,![]() -
решения системы (1), в том числеi-того
уравнения системы (1)
-
решения системы (1), в том числеi-того
уравнения системы (1)
![]()
подставим
эти же числа
![]() ,
,![]() ,…,
,…,![]() в левую частьi-того
уравнения системы (2)
в левую частьi-того
уравнения системы (2)
![]() =
=
![]()
Набор
![]() ,
,![]() ,…,
,…,![]() является решениемi-того
уравнения системы (2), а значит и решением
системы (2), поскольку все остальные
уравнения в (2) такие же как в системе
(1). Так как
является решениемi-того
уравнения системы (2), а значит и решением
системы (2), поскольку все остальные
уравнения в (2) такие же как в системе
(1). Так как
![]() ,
,![]() ,…,
,…,![]() -произвольные
решения системы (1), то всякое решение
системы (1) является решением системы
(2)
-произвольные
решения системы (1), то всякое решение
системы (1) является решением системы
(2)
Заметим, что
систему (1) можно получить из системы
(2) также при помощи преобразования (б).
для этого нужно i-тое
уравнение системы (1) умножить на число
![]() .
В соответствии с доказанным всякое
решение системы (2) будет решением (1)
.
В соответствии с доказанным всякое
решение системы (2) будет решением (1)
выполним преобразование
(в). К i-тому
уравнению системы (1) прибавим j-тое
уравнение
![]() (3) , умноженное на число
(3) , умноженное на число![]() .
Преобразованное в системе (3)j-тое
уравнение будет таким
.
Преобразованное в системе (3)j-тое
уравнение будет таким
![]()
Пусть
![]() ,
,![]() ,…,
,…,![]() -произвольные
решения системы (1), в том числеi-того
и j-того
уравнения
-произвольные
решения системы (1), в том числеi-того
и j-того
уравнения
![]() ,
,
![]()
Подставим этот же набор чисел вместо неизвестных в левую часть j-того уравнения (3)
![]() =
=![]() +
+![]() =
=![]() Это означает, что
Это означает, что![]() ,
,![]() ,…,
,…,![]() -
есть решениеi-того
уравнения системы (3) и всех остальных
решений, так как они такие же как как в
системе (1).
-
есть решениеi-того
уравнения системы (3) и всех остальных
решений, так как они такие же как как в
системе (1).
Билет №11. Решение матричного уравнения AX=B (существование и единственность).
Пусть А - квадр.,
невырожденная, n-порядка,
тогда АХ=В имеет единственное решение,
которое находится по формуле
![]() (1)
(1)
Док-во.
Пусть
![]() -
решение. Подставим
-
решение. Подставим![]() в (1) :
в (1) :![]() .
Умножим обе части на
.
Умножим обе части на![]() :
: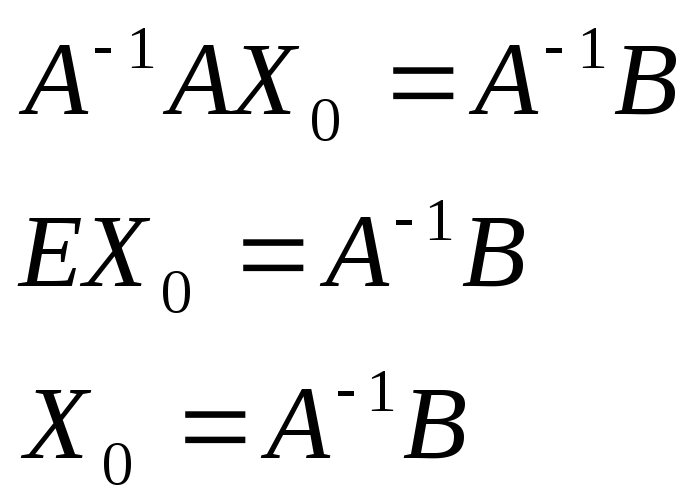
Следовательно, решение существует и оно единственное.
![]()
