15

Билет №15

1. Фундоментальная система решений однородного ур-я – это

совокупность n решений однородного ур-я, определённых и линейно-независимых на интервале (a,b).

Основная теорема об общем решении однородного линейного ур-я.

Если функции y1, y2…yn образуют фундаментальную систему решений линейного однородного ур-я на интервале (a,b), то их линейная комбинация y=, (1) C=const является общим решением этого ур-я.

Д-во. Пусть n=3. y1,y2,y3 - фундоментальная система решений, x ур-я (2)

y

Докажем, что линейная комбинация этих функций

y= (3) является общим решением однородного ур-я при любом наборе С1,С2,С3(это следует из теоремы о свойстве решений однородного лин.ур-я).

Остается показать, что можно подобрать значения С1,С2,С3 так, чтобы ф-я (3) удовлетворяла любой системе начальных условий.

Пусть задана система начальных условий: y=y при .

Обозначим:

y1(x)=(y1), y2(x)=(y2), y3(x)=(y3);

y’1(x)=(y’1), y’2(x)=(y’2), y’3(x)=(y’3);

y”1(x)=(y”1), y”2(x)=(y”2), y”3(x)=(y”3);

Для того, чтобы функция (3) удовлетворяла заданной системе начальных условий, произвольные постоянные должны быть решением системы уравнений:

(4)

Система (4) есть система из трех неоднородных линейных ур-й относительно неизвестных С1, С2,С3.

Определитель это системы:

=w(x) – это вронскиан ф-й y1,y2,y3.

Известно из алгебры, что если определитель системы отличен от 0, то сущ-ет одинественное реш-е.

Согласно опред-ю общего решения уравнения n-ого порядка, ф-я (3) является общим решением однородного ур-я.

2. Интегральный признак Коши сходимости знакоположительных рядов.

Пусть a знакополож. ряд, члены которого не возрастают, т.е.a1a2a3 …;

f(x)- непрерывная невозрастающая функция и такая, что f(1)=a, f(2)=a, …, f(n)=a,… , т.е. данный ряд можно записать .

Тогда:

1. Если несобственный интеграл сходится, то сходится и ряд ;

2. Если 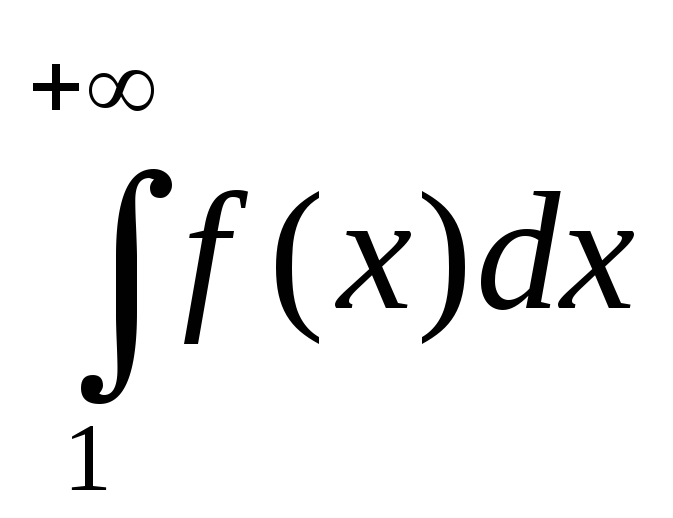расходится, то расходится и ряд