
Лекции по линейной алгебре / 2_Определители квадратных матриц
.pdf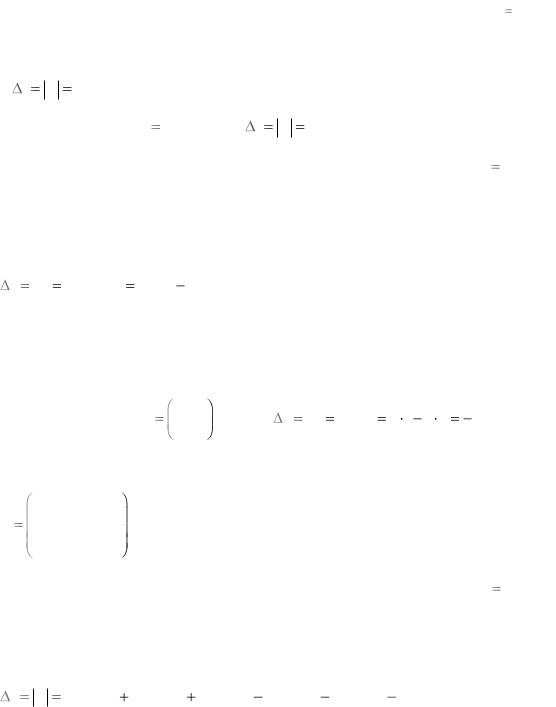
Лекция 2. Определители квадратных матриц и их свойства
План:
1)Правила нахождения определителей;
2)Свойства определителей.
2.2.Правила нахождения определителей
Определение. Определителем матрицы первого порядка А а11 ,или
определителем первого порядка, называется элемент а11 :
1 A a11 .
Например, пусть A 7 , тогда 1 A 7 .
Определение. Определителем матрицы второго порядка A aij , или определителем второго порядка, называется число, которое вычисляется по
формуле:
2 |
|
A |
|
|
a11 |
a12 |
a11a22 |
a12a21. |
|
|
|||||||
|
|
|
a21 |
a22 |
||||
|
|
|
|
|
|
|
Произведения a11a22 и a12a21 называются членами определителя второго порядка.
Например, пусть A |
4 |
9 |
, тогда |
2 |
|
A |
|
|
4 |
9 |
4 1 5 9 41. |
||
|
|
||||||||||||
|
|
|
5 |
1 |
|
|
|
|
|
|
5 |
1 |
|
|
|
|
|
|
|
|
|
|
|||||
Пусть дана матрица третьего порядка: |
|
|
|
|
|
||||||||
a11 |
a12 |
a13 |
|
|
|
|
|
|
|
|
|
|
|
A a21 |
a22 |
a23 . |
|
|
|
|
|
|
|
|
|
|
|
a31 |
a32 |
a33 |
|
|
|
|
|
|
|
|
|
|
|
Определение. Определителем матрицы третьего порядка A aij , или определителем третьего порядка, называется число, которое вычисляется по формуле:
3 A a11a22a33 a12a23a31 a21a32a13 a31a22a13 a12a21a33 a32a23a11 .
Это число представляет алгебраическую сумму, состоящую из 6
слагаемых, или 6 членов определителя. В каждое слагаемое входит ровно по
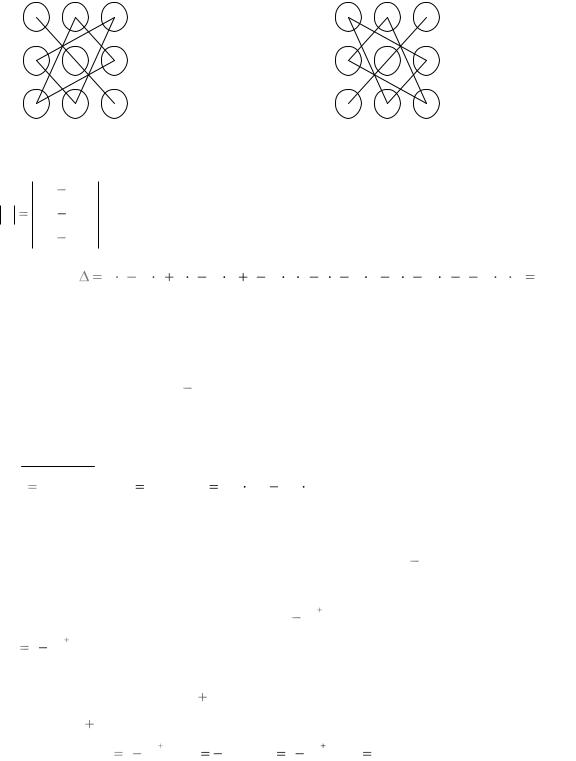
одному элементу из каждой строки и каждого столбца матрицы. Знаки, с
которыми члены определителя входят в формулу, легко запомнить,
пользуясь схемой, которая называется правилом треугольников или
правилом Сарруса.
Пример. Вычислить определитель третьего порядка
2 2 2
A3 3 3 .
1 2 1
Решение. |
|
2 |
3 1 |
3 2 2 |
2 |
3 1 1 |
3 2 |
3 |
2 1 |
2 3 2 0 |
||||
Пусть дана квадратная матрица A n-го порядка. |
|
|
|
|||||||||||
Минором Mij |
элемента aij |
матрицы n-го порядка называется |
||||||||||||
определитель |
матрицы |
n 1 -го порядка, полученной из |
матрицы A |
|||||||||||
вычёркиванием i-й строки и j-го столбца. |
|
|
|
|
||||||||||
Например, минором элемента a11 |
матрицы A третьего порядка будет: |
|||||||||||||
|
|
a11 |
a12 |
a13 |
|
a22 |
a23 |
|
|
a23 a32 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||||
M11 |
|
a21 |
a22 |
a23 |
|
a22 a33 |
|
|
|
|
|
|||
|
|
a32 |
a33 |
|
|
|
|
|
||||||
|
|
a31 |
a32 |
a33 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|||||||||||
Каждая матрица n-го порядка имеет n2 миноров |
n |
1 -го порядка. |
||||||||||||
Алгебраическим дополнением Aij |
элемента aij |
матрицы n-го порядка |
||||||||||||
называется его минор, взятый со знаком |
1 i j |
: |
|
|
|
|||||||||
Aij |
1 i j M ij . |
|
|
|
|
|
|
|
|
|
|
|||
т.е. алгебраическое дополнение совпадает с минором, когда сумма номеров строки и столбца i j - чётное число, и отличается от минора
знаком, когда i j - нечётное число.
Например, A12 1 1 2 M12 M12 ; A13 1 1 3 M13 M13 .

Пример. Найти алгебраические дополнения всех элементов матрицы:
1 2 3 A 1 2 3 .
1 2 3
Решение.
A |
1 1 1 |
2 |
|
3 |
|
|
12; A |
1 1 2 |
|
1 |
3 |
|
|
6; A |
1 1 3 |
1 |
2 |
|
0; |
||||||||
11 |
|
2 |
3 |
|
12 |
|
|
1 |
|
|
3 |
|
13 |
|
1 |
2 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
A |
1 1 2 |
|
|
|
3 |
|
12; A |
1 2 |
2 |
|
1 |
3 |
|
0; A |
1 2 |
3 |
|
1 |
2 |
|
4; |
||||||
|
2 |
|
|
|
|
|
|
||||||||||||||||||||
21 |
|
|
2 |
3 |
|
22 |
|
|
|
|
|
1 |
3 |
|
23 |
|
|
|
1 |
2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
3 |
|
|
|
|
|
1 3 |
|
|
|
|
|
1 2 |
|
|
|
|||||||||
A |
1 3 1 |
|
2 |
|
|
|
0; A |
1 3 2 |
|
|
|
6; A |
1 3 3 |
|
|
4. |
|||||||||||
31 |
|
|
2 |
|
3 |
|
|
32 |
|
1 |
3 |
|
|
33 |
|
1 |
2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Важное значение для вычисления определителей имеет следующая теорема.
Теорема Лапласа. Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения:
|
n |
|
|
ai1 Ai1 |
ai 2 Ai 2 ain Ain |
ais Ais . |
|
|
s |
1 |
|
(разложение по элементам i-й строки; i |
1;2; ; n ); |
||
|
|
n |
|
a1 j A1 j |
a2 j A2 j anj Anj |
asj Asj . |
|
|
|
s 1 |
|
(разложение по элементам j-й строки; j |
1;2; ; n ). |
||
2.2 Свойства определителя
1.Если какая-либо строка (столбец) матрицы состоит из одних нулей, то её определитель равен 0.
2.Если все элементы какой-либо строки (столбца) матрицы умножить на число , то её определитель умножиться на это число 
Пусть определитель исходной матрицы равен . Для определённости
первую строку матрицы умножим на |
, получим новый определитель , |
|||||||||
который |
|
разложим |
|
по |
элементам |
первой |
строки: |
|||
|
a11 |
a12 |
|
a1n |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
a21 |
a22 |
|
a2n |
|
a11 A11 |
a12 A12 |
a1n A1n |
a11 A11 a12 A12 |
a1n A1n |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
||||
|
an1 |
an 2 |
|
ann |
|
|
|
|
|
|
Замечание. За знак определителя можно выносить общий множитель любой строки или столбца. Но у матрицы, за знак можно выносить общий множитель лишь всех элементов.

|
|
|
|
|
6 |
8 |
4 |
|
3 |
4 |
2 |
|
3 |
2 |
2 |
|
3 |
2 |
2 |
|
Например, |
|
|
1 |
2 |
1 |
2 |
1 |
2 |
1 |
2 2 |
1 |
1 |
1 |
2 2 2 |
1 |
1 |
1 |
, но |
||
|
|
|
|
|
8 |
4 |
4 |
|
8 |
4 |
4 |
|
8 |
2 |
4 |
|
4 |
1 |
2 |
|
6 |
8 |
4 |
|
3 |
4 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
1 |
2 |
0, 5 |
1 |
0, 5 . |
|
|
|
|
|
|
|
|
|
|
|
|||
8 |
4 |
4 |
|
4 |
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3.При транспонировании матрицы её определитель не
изменяется: AT A .
4.При перестановке двух строк (столбцов) матрицы её определитель меняет знак на противоположный.
5.Если квадратная матрица содержит две одинаковые строки (столбца), то её определитель равен 0.
6.Если элементы двух строк (столбцов) матрицы пропорциональны, то её определитель равен 0.
7.Сумма произведений элементов какой-либо строки (столбца)
матрицы на алгебраические дополнения элементов другой строки
n |
|
(столбца) этой матрицы равна 0, т.е. |
ais Ais 0 при i j . |
S |
1 |
8.Определитель матрицы не изменится, если к элементам какойлибо сроки ( столбца) матрицы прибавить элементы другой строки (столбца), предварительно умноженные на одно и то же число.
9.Определитель произведения двух квадратных матриц равен
произведению их определителей: C 
 A
A
 B , где C A B ; А и В - матрицы n-го порядка
B , где C A B ; А и В - матрицы n-го порядка
