Лекции по линейной алгебре / 8_ прямая и плоскость в пр

Лекция 8. Условия параллельности и перпендикулярности прямых. Прямая и плоскость в пространстве

План:

1. Взаимное расположение прямых на плоскости;

2. Уравнение плоскости в пространстве;

3. Прямая в пространстве;

4. Примеры решения задач.

8.1. Взаимное расположение прямых на плоскости

Угол между двумя прямыми. Пусть заданы две прямые на плоскости: (1) и (2) и требуется определить угол между ними (см. рис. 8.1).

Рис. 8.1. Угол между двумя прямыми

Из рис. 8.1. видно, что , причем и , .

Тогда или

. (8.1)

Условия параллельности и перпендикулярности прямых.

Пусть заданы две прямые:

(1);

(2).

Прямые (1) и (2) параллельны тогда и только тогда, когда .

Если прямые перпендикулярны, то и .

Прямые (1) и (2) перпендикулярны тогда и только тогда, когда .

Пусть прямые заданы общими уравнениями:

(1);

(2).

В этом случае угловые коэффициенты и и условие параллельности примет вид:

Прямые (1) и (2) параллельны тогда и только тогда, когда .

Следовательно, условием параллельности прямых, заданных общими уравнениями, является пропорциональность коэффициентов при переменных.

Условием перпендикулярности двух прямых, заданных общими уравнениями, является равенство нулю суммы произведений коэффициентов при переменных и .

Действительно, т.к. , то .

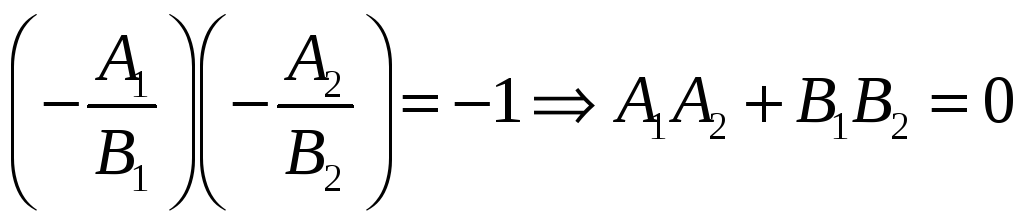Прямые (1) и (2) перпендикулярны тогда и только тогда, когда .

Точка пересечения прямых.

Пусть прямые заданы общими уравнениями: и .

Так как координаты точки пересечения должны удовлетворять каждому из уравнений, то их можно найти из системы: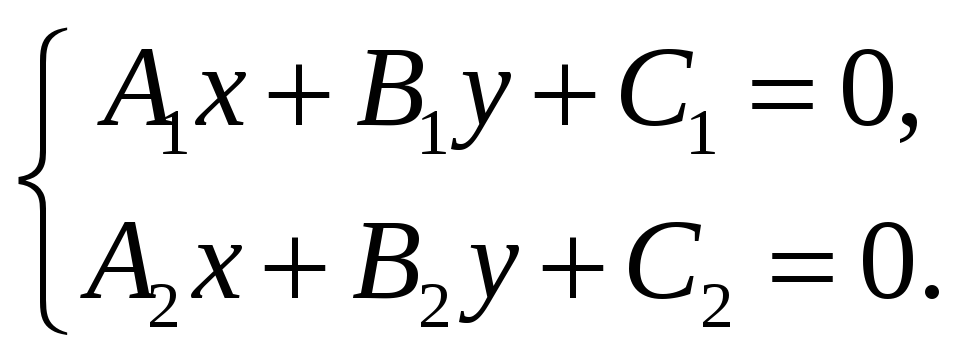

Расстояние от точки до прямой.

Пусть даны точка и прямая .

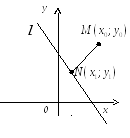
Рис. 8.2. Расстояние от точки до прямой

Под расстоянием от точки до прямой понимается длина перпендикуляра , опущенного из точки на прямую (рис. 8.2).

Для нахождения расстояния необходимо:

1. составить уравнение прямой , перпендикулярной данной и проходящей через точку ;

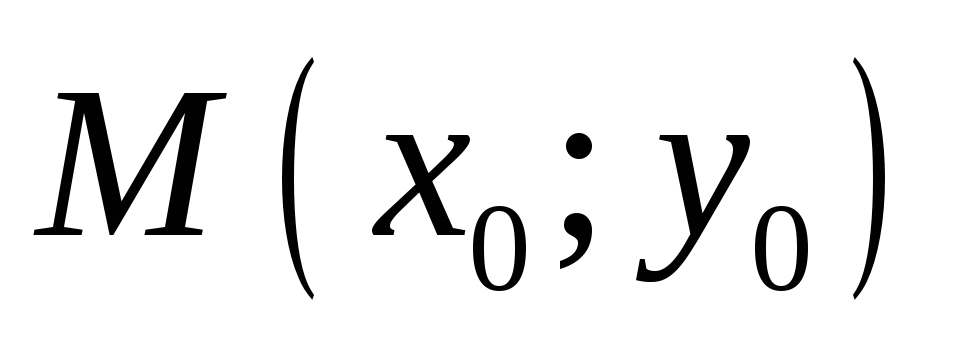2. найти точку 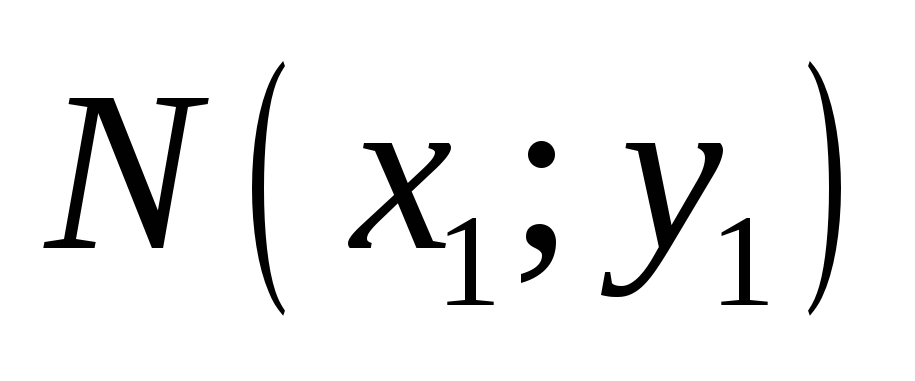пересечения прямых, решив систему уравнений этих прямых;

3. найти 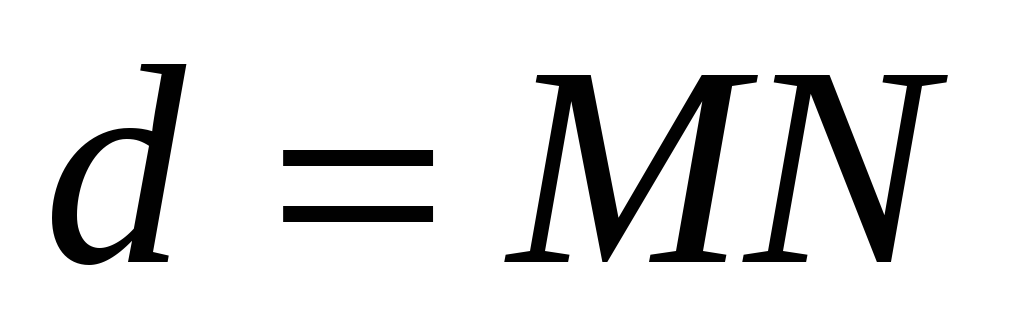по формуле расстояния между двумя точками.

В итоге получается формула:

. (8.2)

8.2. Уравнение плоскости в пространстве

а) Задание плоскости по точке и нормальному вектору. Пусть плоскость проходит через точку перпендикулярно вектору (рис.8.3).

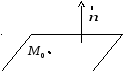
Рис. 8.3. Плоскость, заданная точкой и нормальным вектором

Вектор называется нормальным вектором плоскости .

Возьмем в плоскости произвольную точку . Тогда вектор будет перпендикулярен вектору . Значит скалярное произведение этих векторов равно нулю, т.е. в координатном виде:

; (8.3)

.

Уравнение плоскости можно записать в виде:

, (8.4)

где .

Уравнение (8.4) называется общим уравнением плоскости.

б) Задание плоскости по трем точкам. Возьмем на плоскости три точки, не лежащие на одной прямой: , , .

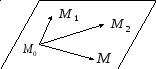
Рис. 8.4. Задание плоскости по трем точкам

Зададим векторы и . Так как три данные точки не лежат на одной прямой, то заданные векторы не коллинеарные (не параллельны и не лежат на одной прямой). Векторы и образуют базис двумерного пространства.

В плоскости возьмем произвольную точку . Зададим вектор . Так как векторы и образуют базис, то вектор является линейной комбинацией базисных векторов. Значит, строки матрицы, составленной из координат этих векторов, линейно зависимы и определитель такой матрицы равен нулю:

. (8.5)

в) Задание плоскости по точке , лежащей на плоскости и двум направляющим векторам (векторы лежат в данной плоскости или параллельны плоскости) и .

Рассуждения аналогичны рассуждениям под буквой б), поэтому получим:

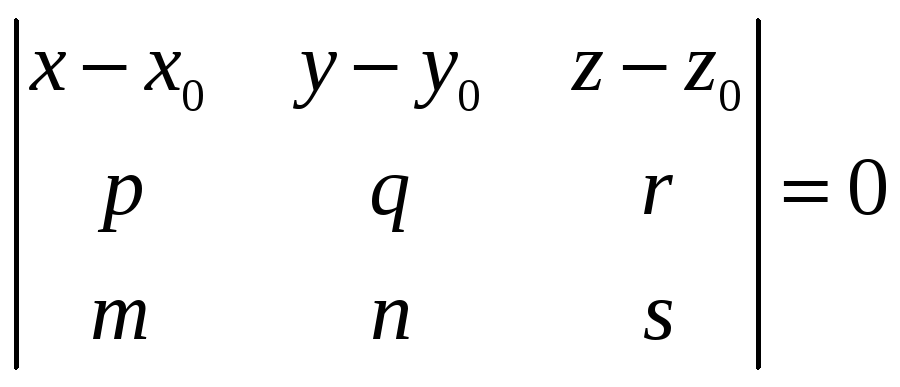. (8.6)

Частные случаи общего уравнения плоскости :

Если , то уравнение определяет плоскость, проходящую через начало координат.

Если , то уравнение определяет плоскость, параллельную . Аналогично при параллельность и при параллельность .

Если , то определяет плоскость, параллельную плоскости . При параллельность , при параллельность .

Если , то определяет плоскость, проходящую через ось . При проходит через , при проходит через .

Если , то определяет координатную плоскость . При плоскость , при плоскость .

Условия параллельности и перпендикулярности плоскостей определяются условиями коллинеарности и перпендикулярности нормальных векторов и .

Условием параллельности двух плоскостей является пропорциональность коэффициентов при одноименных переменных:

.

Условие перпендикулярности:

.

8.3. Прямая в пространстве

а) Прямая в пространстве может быть задана, как линия пересечения двух плоскостей:

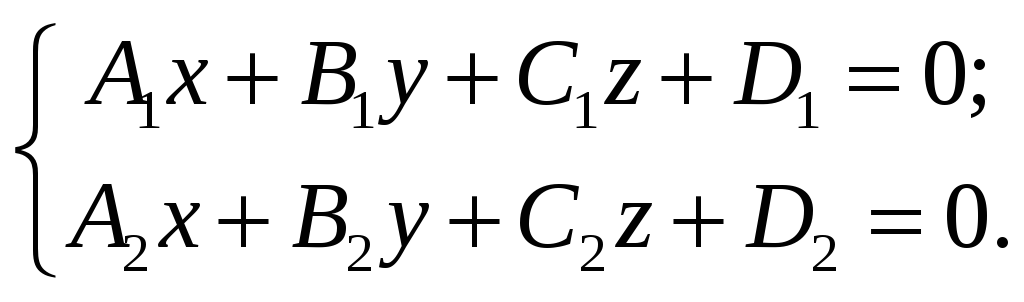
б) Если прямая параллельна вектору (направляющий вектор) и проходит через точку , то из условия коллинеарности векторов и (где - произвольная точка прямой) получим:

. (8.7)

Уравнения (8.7) называются каноническими уравнениями прямой линии в пространстве.

в) Уравнения (8.7) можно записать в параметрическом виде:

;

Приравнивая каждую дробь к параметру , получим:

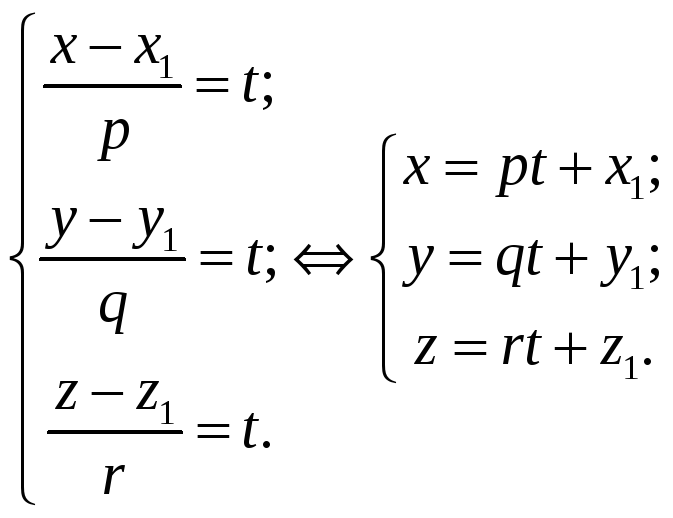(8.8)

Уравнения (8.8) называются параметрическими уравнениями прямой в пространстве.

8.4. Примеры решения задач

Пример 1. Составить уравнение прямой, проходящей через точку :

а) параллельно прямой : ;

б) перпендикулярно прямой : .

Решение.

а) Так как искомая прямая параллельна прямой : , то . Найдем исходной прямой . Откуда получим, что .

Итак, искомую прямую задаем по точке и угловому коэффициенту :

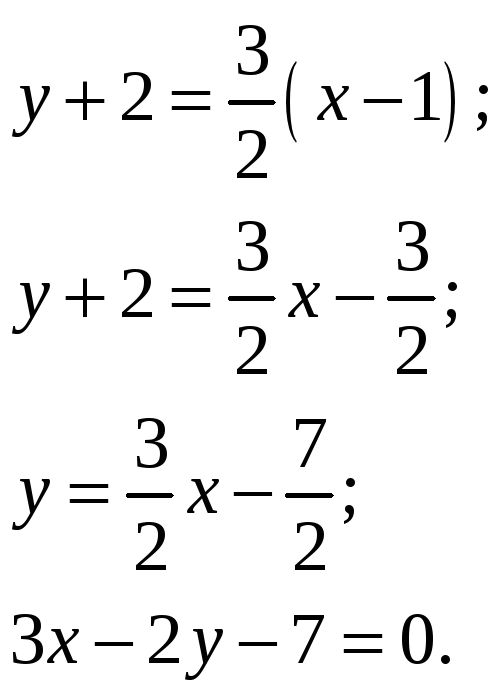
б) Так как искомая прямая перпендикулярна прямой : , то . Из уравнения исходной прямой получаем . Тогда .

Уравнение искомой прямой:

Ответ: а) ; б) .

Пример 2. Составить уравнение плоскости , проходящей через точку и :

а) параллельной плоскости : ;

б) точку , параллельной оси ;

в) проходящей через ось .

Решение.

а) Так как искомая плоскость параллельна плоскости , то нормальный вектор последней плоскости будет нормальным вектором и для искомой плоскости. Значит, и для задания уравнения используем формулу (8.3):

б) Так как плоскость параллельна , то в общем уравнении (8.4) коэффициент , и уравнение имеет вид . Так как точки и лежат на плоскости, то их координаты должны удовлетворять уравнению плоскости:

Следовательно, уравнение плоскости имеет вид:

в) Так как плоскость проходит через ось , то , т.е. уравнение плоскости имеет вид . Так как плоскость содержит точку , то . Уравнение плоскости запишется:

Ответ: а) ; б) ; в) .