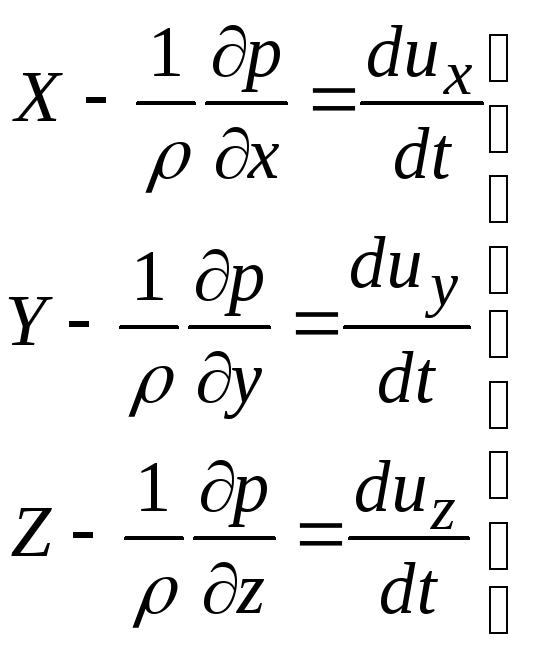Гидравлика Уравнения неразрывности, Эйлера, Бернулли 08-10

Уравнение неразрывности (сплошности) для несжимаемой жидкости в дифференциальной форме.

Гидродинамика.

Дифференциальные уравнения движения идеальной жидкости Л. Эйлера.

Уравнение Д. Бернулли для элементарной струйки идеальной (невязкой) и реальной (вязкой) жидкости и газов.

Уравнение Д. Бернулли для всего потока реальной жидкости и газа и его интерпретация.

Понятие об уклонах.

Уравнение неразрывности для несжимаемой жидкости в дифференциальной форме

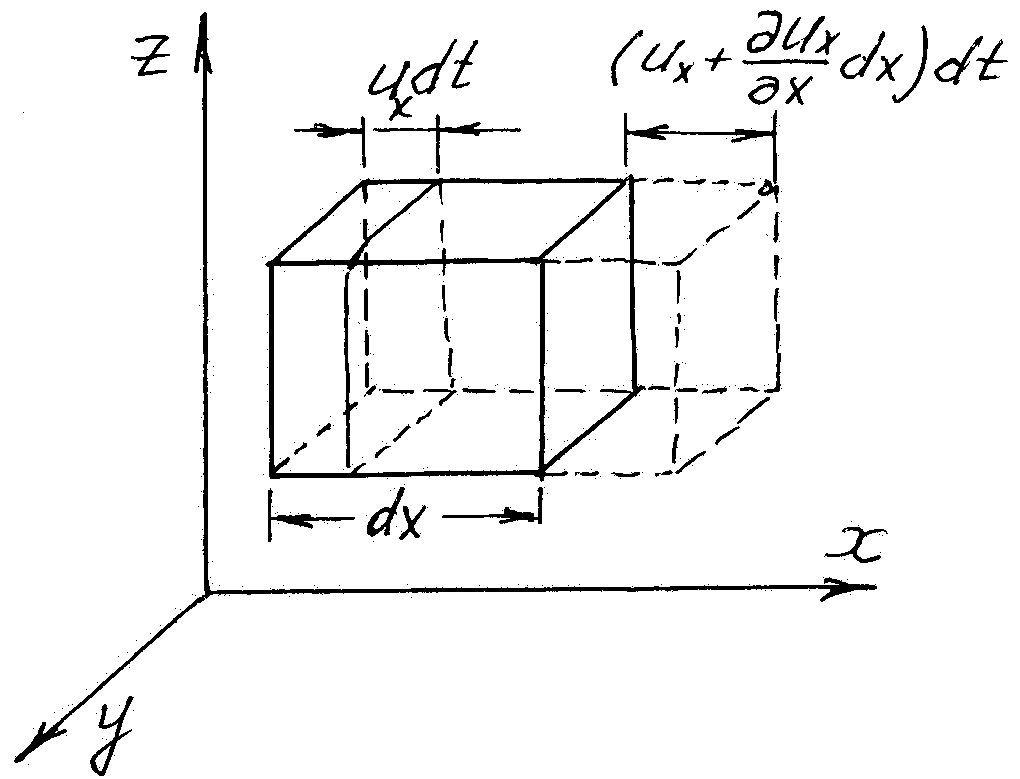
Выделим в области, занятой движущейся жидкостью, неподвижный бесконечно малый параллелепипед (кубик), у которого ребра параллельны соответствующим осям координат. Выделенный кубик неподвижен в пространстве, а через его грани протекает несжимаемая жидкость. Очевидно, что масса входящей за время жидкости равна массе выходящей за то же время жидкости.

Сначала рассмотрим грани перпендикулярные оси , левую и правую.

Их площадь одинакова: .

Скорость втекающей через левую грань жидкости можно считать одинаковой по всей грани. Тогда за время через левую грань войдет масса .

По гипотезе сплошности скорость жидкости есть непрерывная дифференцируемая функция своих аргументов. Тогда скорость жидкости на правой грани, которая отстоит от левой на расстояние составит .

Выходящая за время через правую грань масса .

Изменение массы жидкости в объеме параллелепипеда за счет входа и выхода жидкости через левую и правую грани:

Аналогичные выражения могут быть получены по двум другим осям, т.е. по двум другим парам граней. Общее изменение массы следует приравнять нулю:

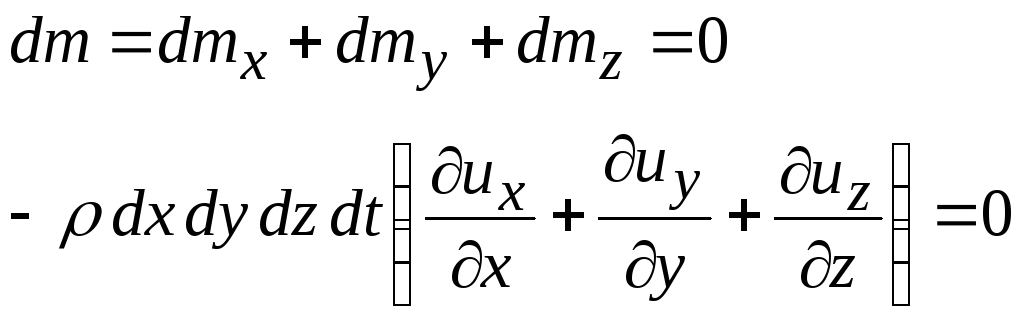
Понятно, что левая часть равна нулю только если выражение в скобках равно нулю.

Уравнение неразрывности для несжимаемой жидкости в дифференциальной форме.

Из математики известно : ,

где – дивергенция ( расходимость) векторного поля в данной точке.

( Для справки. Определение. Предел отношения потока П поля через некоторую замкнутую поверхность S к объему, ограниченному поверхностью S, когда S стягивается в точку М, называется дивергенцией, или расходимостью, поля в точке М.)

Другая форма записи уравнения неразрывности …

Попытаемся найти геометрический смысл слагаемых вида .

Рассмотрим грань (ребро кубика). Скорость левого ее конца , а скорость правого конца . За время ребро не только переместится в пространстве, но и за счет разности скоростей его концов удлинится (деформируется) на величину . Скорость удлинения ребра составит , а относительная скорость деформации ребра можно найти, если поделить эту скорость на длину грани . Получим .

Уравнение неразрывности для несжимаемой жидкости в дифференциальной форме можно истолковать так: сумма скоростей относительной деформации ребер жидкой частицы равна нулю. Жидкость движется так, что данная масса все время занимает один и тот же объем.

ГИДРОДИНАМИКА

Гидродинамика изучает движение жидкости с учетом сил, вызывающих это движение.

Массовые внешние силы, действующие на жидкость, как правило известны и заданы проекциями плотности распределения равнодействующей на оси координат .

Плотность жидкости полагается постоянной и известной.

Задача гидродинамики – определить кинематические характеристики движения и возникающие напряжения, т.е. найти зависимость величин и давления от координат и времени.

Дифференциальные уравнения движения идеальной жидкости Л. Эйлера

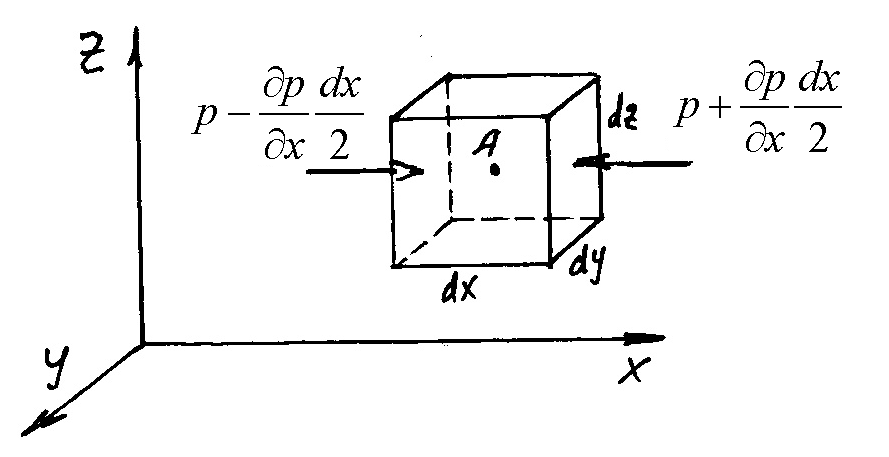
Рассмотрим элементарный параллелепипед (кубик) жидкости с ребрами , параллельными осям координат. Эта жидкая частица движется относительно неподвижной системы координат. Точка А – полюс (в центре тяжести).

Воспользуемся вторым законом Ньютона применительно к жидкой частице. Произведение массы частицы на ускорение ее центра масс равно сумме всех внешних сил, действующих на частицу. Силы и ускорение будем рассматривать в проекции на оси координат (на ось рассмотрим, на остальные аналогично).

Масса частицы : .

Ускорение в проекции на ось :

Поверхностные силы – это силы нормального давления окружающей частицу жидкости. Они равны произведению давления на площадь грани. Рассмотрим грани, перпендикулярные оси , их площадь . Пусть в полюсе давление равно .

Давление на левую грань , на правую грань .

Сила на левую грань , на правую грань .

Равнодействующая поверхностных сил в проекции на ось : .

Массовые силы в проекции на ось : .

Сумма сил равна произведению массы на ускорение ( в проекции на ось ):

Разделим на массу и аналогично запишем проекции на другие оси

Дифференциальные уравнения движения невязкой жидкости Л. Эйлера (1755 г.)

Можно развернуть выражение для ускорения, учитывая что скорость есть не только функция времени, но и координат. При описании метода Эйлера на прошлой лекции было получено выражение (например – в проекции на ось :

Дифференциальные уравнения движения невязкой жидкости в развернутом виде запишутся:

В задачах динамики неизвестными являются функции

– давления

– проекции скорости , ,

– и плотность

всего пять неизвестных.

Для определения неизвестных используется система уравнений Эйлера. Поскольку число неизвестных превышает число уравнений, к системе добавляют уравнение неразрывности и уравнение состояния среды (зависимость плотности от давления).

Для несжимаемой жидкости уравнение состояния

и уравнение неразрывности

Общего решения полученной системы уравнений нет, только частные решения для специальных задач.