Местные сопротивления 11-5

Общая классификация сопротивлений: сопротивление трения (по длине) и местные.

Суммируемость гидравлических сопротивлений.

Местные сопротивления.

Общая методика их учета.

Коэффициент местного сопротивления и факторы, влияющие на его величину.

Зависимость коэффициентов местных сопротивлений от числа Рейнольдса.

Гидравлические сопротивления

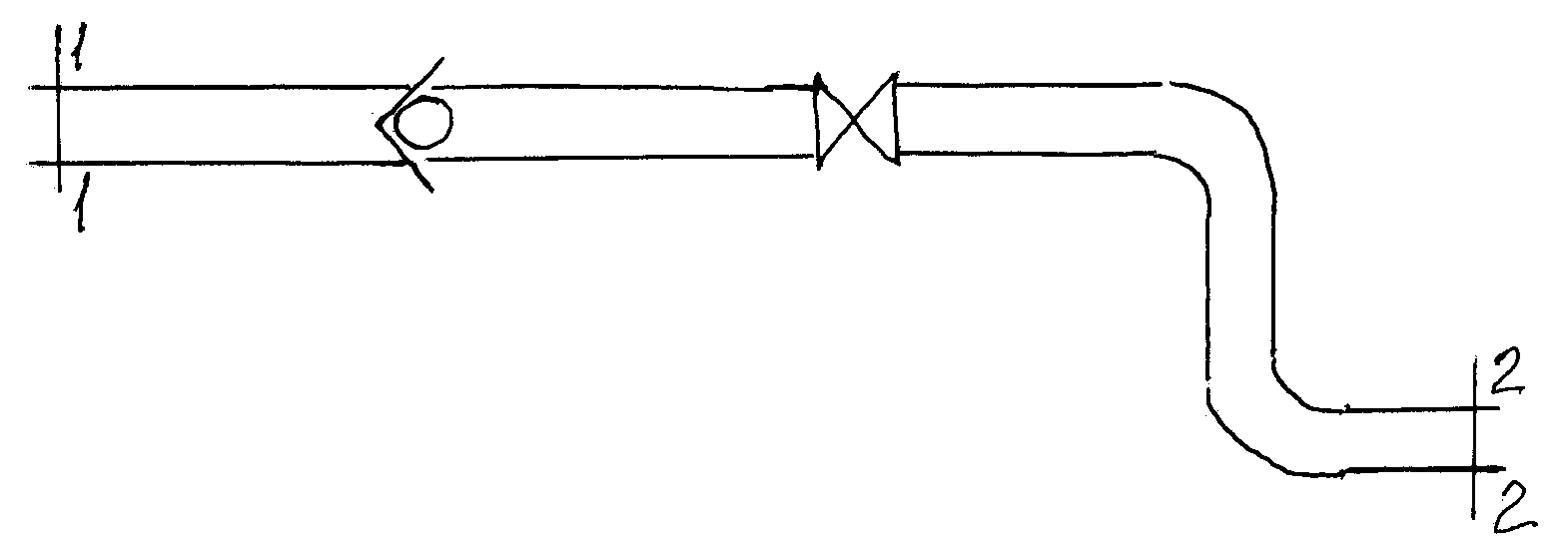
Рассмотрим трубопровод, состоящий из нескольких прямых участков постоянного диаметра и местных сопротивлений: обратного клапана, задвижки и двух плавных поворотов на 90.

Для сечений 1-1 и 2-2 потока может быть записано уравнение Бернулли, из которого выразим потери полного напора:

.

Это общие потери от сечения 1-1 до сечения 2-2 , которые могут рассматриваться как сумма потерь по длине прямолинейных участков постоянного диаметра и потерь в местных сопротивлениях.

(*)

Такое разделение – основное допущение при расчете потерь в трубопроводах.

Забегая вперед, отметим, что эти два типа потерь рассчитываются отдельно.

Потери по длине по экспериментальной формуле Дарси¹ (Дарси-Вейсбаха)

, (*)

здесь – коэффициент гидравлического сопротивления (коэффициент Дарси).

Потери в местных сопротивлениях есть сумма отдельных потерь, каждая из которых вычисляется по формуле Вейсбаха:

, (*)

здесь – коэффициент местного сопротивления номер , определяется из справочников.

(– «дзета», греч. не путать – «кси», греч.)

Местные сопротивления

– места потока, в которых происходит резкая его деформация, скорость изменяется по величине и по направлению.

	Для того чтобы измерить потери напора в местном сопротивлении поступают так: 1. производят замер потерь напора на местном сопротивлении, причем пьезометры устанавливают не рядом с ним, а на расстоянии не менее , где поток невозмущенный.
	2. производят замер потерь на участке того же трубопровода длиной без местного сопротивления 3. вычисляют

4. Учитывая, что , находят коэффициент местного сопротивления

Такой способ замера позволяет выделить отдельно влияние местного сопротивления.

Расчетным путем найти коэффициент местного сопротивления не удается, единственное исключение – внезапное расширение потока.

Внезапное расширение потока

Рассмотрим внезапное расширение круглого трубопровода, выделим сечения 1-1 и 2-2. Площади живых сечений потока и , скорости и .

Составим уравнение Бернулли для сечений 3-3 и 2-2, принимая скорость потока в сечении 3-3 равной и учитывая, что .

здесь – потери напора на внезапном расширении.

Принимаем , находим потери

Применим к массе жидкости, заключенной между сечениями 3-3 и 2-2 теорему о количестве движения, согласно которой изменение количества движения в единицу времени равно сумме внешних сил. Допускаем, что во всем сечении 3-3 действует давление .

Отсюда выразим

и подставим в выражение для потерь

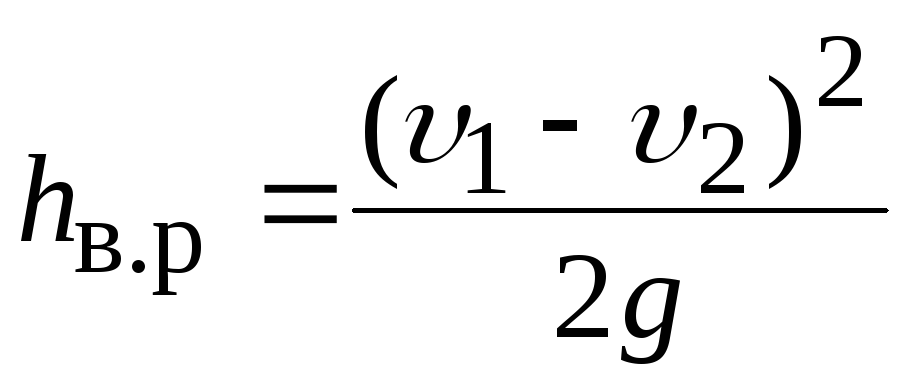
Формула Бордá : потери напора при внезапном расширении потока пропорциональны квадрату «потерянной» скорости2

Приведем это выражение к виду формулы Вейсбаха для местных сопротивлений:

По уравнению неразрывности для потока т.е.

Коэффициент сопротивления (отнесенный к скорости до расширения)

В предельном случае, когда , имеем выход из трубопровода в резервуар больших размеров, .

Так как скорость до расширения не равна скорости после него , то для данного местного сопротивления существует два различных значения коэффициента сопротивления, расчет потерь напора с использованием которых, разумеется, приводит к одинаковому результату.

. Легко показать, что

Другие коэффициенты местных сопротивлений:

Коэффициенты местных сопротивлений приводятся в справочниках

И.Е. Идельчик Справочник по гидравлическим сопротивлениям

Справочник по гидравлическим расчета под ред. П.Г. Киселева

Плавный поворот на 90 при ( Идельчик, стр. 184)

В расчетах, если не задан радиус поворота, принимать потери по длине трубы добавлять.

Диафрагма (диск с отверстием диаметра меньше, чем диаметр трубы)

	0,1	0,5	0,9	1
	245	4	0,13	0

Внезапное сужение потока , и диаметры трубы до и после.

Вход из бака в трубу, когда >>, .

Влияние числа Re на коэффициенты местных сопротивлений

Коэффициенты в справочниках даются для квадратичной области сопротивления турбулентного режима (не зависят от Re).

Для ламинарного режима

Re – число Рейнольдса, А – коэффициент, характеризующий тип местного сопротивления, приводится в справочниках

Сопротивление
Пробочный кран	150	0,4
Колено 90	130	0,2
Выход из трубы в бак	30	1
Вход из бака в трубу	30	0,5

Взаимное влияние местных сопротивлений

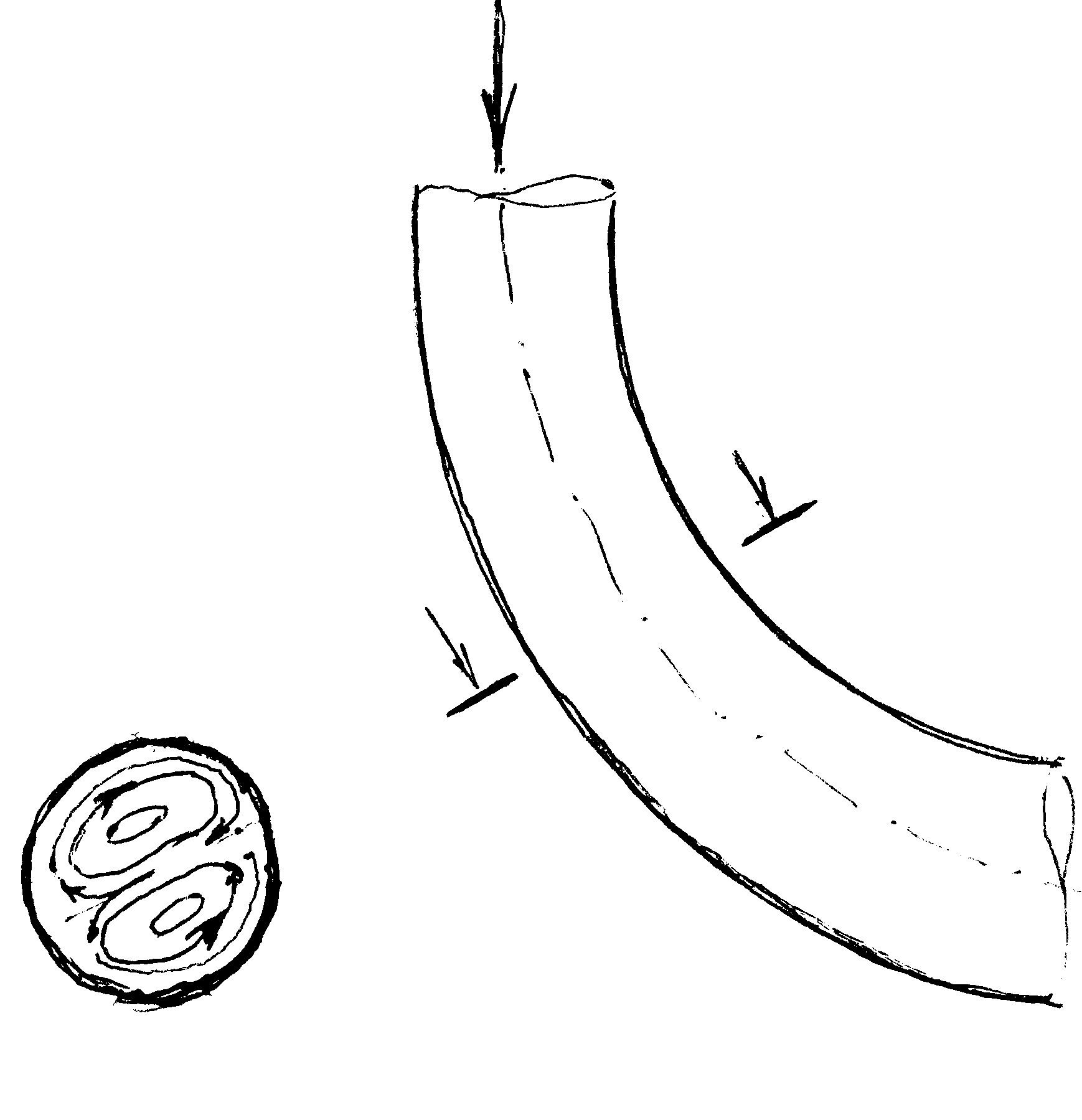
Плавный поворот потока При изменении направления потока появляются центробежные силы, направленные от центра кривизны к внешней стенке трубы. Давление в пределах поворота у внешней стенки больше, чем у внутренней. Соответственно скорости у внешней стенки меньше, чем у внутренней. Вследствие этого вдоль боковых стенок трубы, вблизи поверхности которых скорость невелика, будет происходить движение жидкости от внешней стенки к внутренней, т.е. возникает поперечная циркуляция в потоке.

В результате образуется так называемый парный (двойной) вихрь, который накладывается на поступательное движение. Линии тока становятся винтообразными. Эпюра скоростей в связи с этим перестраивается.

Если местные сопротивления расположены на близком расстоянии друг от друга, то они влияют друг на друга.

Так например, при последовательном соединении двух отводов (отвод-поворот на 90о, рисунок VI-2) суммарный коэффициент сопротивления в случае а) , а в случае б) 3

Здесь – коэффициент сопротивления изолированного поворота на 90, зависит от отношения радиуса поворота к диаметру трубопровода . В справочниках приводятся коэффициенты сопротивления для отвода без учета потерь по длине трубы, которые рассчитываются дополнительно, причем длина считается по средней линии потока.

Длина зоны влияния ,

где – диаметр трубопровода; – коэффициент потерь для данного местного сопротивления в квадратичной области; – коэффициент Дарси.

В обычных условиях длина прямолинейного участка трубопровода между сопротивлениями, равная , оказывается достаточной для стабилизации потока. В ответственных случаях, например при установке расходомерных устройств, эта длина определяется правилами установки и составляет .

Эквивалентная длина. Для упрощения расчета трубопроводов часто используют понятие о эквивалентной длине местного сопротивления, т.е. об участке данного трубопровода такой длины, на которой потери напора по длине равны местной потере напора: => =>

В заключение раздела о местных сопротивлениях отметим, что в гидравлически длинных трубопроводах (или просто длинных) потери по длине настолько превышают потери в местных сопротивлениях, что последние не вычисляют, а принимают как некоторую часть потерь по длине (добавляют 5 % – 10 %).

1 Эту формулу называют формулой Дарси-Вейсбаха, однако во избежание путаницы оставим только первую часть, опираясь на то, что коэффициент называют коэффициентом Дарси.

2 БОРДА (Borda), Жан Шарль (4.5.1733-19.2.1799)

Французский физик и геодезист. Член Парижской АН. Служил офицером сначала в армии, а затем во флоте. Участвовал в разработке метрической системы мер. Определил в 1792 длину секундного маятника в Париже и нашел способ точного определения периода качаний маятника. Предложил в 1766 особую насадку, названную его именем, для увеличения расхода жидкости, вытекающей из сосуда, при заданном сечении выходного отверстия. Доказал носящую его имя теорему в гидравлике об ударе струи жидкости или газа.

3 Идельчик И.Е. Справочник по гидравлическим сопротивлениям, стр. 188, табл. 6-7, 6-8