Координатная матрица узлов рамы

№ узла	Координаты		Сосредоточенные силы			Закрепления по
	x	y			M	x	y	φ
1	0	0	0	0	0	-1	-1	-1
2			0	0	0	0	0	0
3	3,8	4			0	0	0	0
4	3,8	4	0	0	0	3	3	0
5	3,8	4	0	0	0	3	3	0
6	3,8	0	0	0	0	-1	-1	-1
7	6,2	4	0	0	M	0	0	0
8	7,2	0	0	0	0	-1	-1	0

В последних трех столбцах 0 – соответствует свободному перемещению узла в данном направлении, а (-1) - закрепленному, в соответствии с направлением оси, целые положительные числа указывают на номер узла, у которого данное перемещение должно быть одинаковым с текущим узлом.

Топологическая матрица содержит информацию об элементах конструкции и представляет собой таблицу, столбцы которой соответствуют локальным номерам узлов начала и конца элемента, а строки номеру элемента. Внутренние ячейки таблицы содержат глобальные номера узлов, соответствующие каждому элементу, кроме этой информации в каждую строку добавляем характеристики распределенных сил и прочностные и массовые свойства элементов.

Для конструкции рисунка 4.2 топологическая матрица примет вид таблицы 4.2.

Таблица 4.2

Топологическая матрица элементов рамы

№ элемента	Узлы		Значения px в узлах		Значения pyв узлах		EF	EI	m
	1 нач.	2 кон.	1 нач.	2 кон.	1 нач.	2 2 кон.
1	1	2	0	0	0	0	200000	4000	100
2	2	3	0	0	-400	-400	200000	4000	100
3	5	6	0	0	0	0	200000	4000	100
4	4	7	0	0	0	0	200000	4000	100
5	7	8	0	0	0	0	200000	4000	100

По координатной и топологической матрицам формируется матрица индексов – это таблица, строки которой соответствуют номерам элементов, а столбцы локальным номерам обобщенных перемещений. Внутренние ячейки содержат глобальные номера обобщенных перемещений:

Таблица 4.3

Матрица индексов перемещений узлов рамы

№ элемента	Номера перемещений Начальный узел Конечный узел
	1 (u1)	2 (v1)	3 (φ1)	4 (u2)	5 (v2)	6 (φ2)
1	1	2	3	4	5	6
2	4	5	6	7	8	9
3	13	14	15	16	17	18
4	10	11	12	19	20	21
5	19	20	21	22	24	24

По топологической и координатной матрицам вычисляются также направляющие косинусы и длины элементов (формулы (3),(4),(5)) и матрицы жесткости каждого элемента в отдельности (1). В строках матрицы указаны глобальные номера узловых перемещений конечных элементов в порядке следования соответствующих им локальных номеров. Число строк в матрицеравно числу конечных элементовf1.m:

for (int i = 0; i < f1.m; i++)

{

// Формирование матрицы индексов

A[i, 0] = i + 1;

A[i, 1] = Convert.ToInt32(f1.MatrTop[i, 1]) * 3 - 2;

A[i, 2] = Convert.ToInt32(f1.MatrTop[i, 1]) * 3-1;

A[i, 3] = Convert.ToInt32(f1.MatrTop[i, 1]) * 3;

A[i, 4] = Convert.ToInt32(f1.MatrTop[i, 2]) * 3-2;

A[i, 5] = Convert.ToInt32(f1.MatrTop[i, 2]) * 3-1;

A[i, 6] = Convert.ToInt32(f1.MatrTop[i, 2]) * 3;

}

Затем с помощью матрицы индексов суммируем элементы отдельных матриц элементов в общую матрицу жесткости системы. Ниже приведен фрагмент программы на языке С# реализующий процесс сборки:

for (int ii = 0; ii < f1.m; ii++)

{

...//Формирование матрц элемента

for (int i = 1; i <= 6; i++)

{

int ig = A[ii, i];

for (int j = 1; j <= 6; j++)

{

int jg = A[ii, j];

K[ig - 1, jg - 1] = K[ig - 1, jg - 1] + Ke1[i - 1, j - 1];

M[ig - 1, jg - 1] = M[ig - 1, jg - 1] + Me1[i - 1, j - 1];

}

}

}

Обозначения в программе:

6. ii – номер текущего конечного элемента;

7. f1.m– число конечных элементов;

8. A – матрица индексов перемещений;

9. i, j– локальные индексы узловых перемещений конечного элемента;

10. ig, jg– соответствующие им глобальные индексы, выбираемые из матрицыA;

2. K–матрица жесткости конструкции;

2. Ke1– матрица жесткости текущего конечного элемента с номеромii, вычисленная в глобальной системе координат.

Аналогично формируется матрица масс Mконструкции при решении динамической задачи.

Учет граничных условий

Граничные условия делятся на естественные и главные. В качестве естественных граничных условий выступают внешние силы, которые входят в правую часть уравнений равновесия. Для формирования вектора нагрузки организуем цикл с обходом узлов рамы в координатной матрице и добавим в его ячейки силы из четвертого, пятого и шестого столбцов таблицы в соответствии с номерами обобщенных перемещений. Кроме того в столбец обобщенных сил необходимо добавить вклад от распределенных сил, указанных в топологической матрице для каждого элемента, приведенный по выражению (4.8) к глобальным осям координат.

Главные граничные условия – это условия закрепления конструкции. При наложении условий закрепления, то есть уменьшении количества степе­ней свободы системы, уравнения не вычеркивают, а заменяют фиктивными для сохранения нумерации в матрицах. Один из способов состоит в обнулении всех элементов строки, кроме диагонального для данного элемента и обнуление соответствующего элемента столбца нагрузки.

Если перемещения в закрепленных узлах не равны нулю, то их действительные значения, умноженные на диагональный элемент матрицы жесткости, помещают в соответствующую строку вектора нагрузки.

Когда в матрице узлов в столбцах 7,8,9 стоят (-1) – это означает закрепление данного узла по соответствующему направлению: x,y,φ.

for (int i = 0; i < f1.n; i++)

{

//Наложение главных граничных условий для неподвижных опор

if (Convert.ToInt32(f1.MatrCoor[i, 6]) < 0)

{

for (int j = 0; j < f1.n * 3; j++)

{

K1[3 * i, j] = 0;

}

K1[3 * i, 3 * i] = K[3 * i, 3 * i];

P[3 * i] = 0;

}

if (Convert.ToInt32(f1.MatrCoor[i, 7]) < 0)

{

for (int j = 0; j < f1.n * 3; j++)

{

K1[3 * i + 1, j] = 0;

}

K1[3 * i + 1, 3 * i + 1] = K[3 * i + 1, 3 * i + 1];

P[3 * i + 1] = 0;

}

if (Convert.ToInt32(f1.MatrCoor[i, 8]) < 0)

{

for (int j = 0; j < f1.n * 3; j++)

{

K1[3 * i + 2, j] = 0;

}

K1[3 * i + 2, 3 * i + 2] = K[3 * i + 2, 3 * i + 2];

P[3 * i + 2] = 0;

}

}

Случай, когда в столбцах 7,8,9 стоят нули, означает отсутствие закрепления.

Если в ячейках этих столбцов стоят положительные целые числа, то это означает, что данное перемещение равно перемещению узла по соответствующему направлению, с номером, указанным в ячейке.

Такое явление возникает при наличии в системе внутренних шарниров, муфт и других видов связей. При этом внешние силы, приложенные в шарнире во всех узлах, прикладывают к одному из узлов, примыкающему к шарниру. Коэффициенты, стоящие вне главной диагонали в матрицы жесткости для других узлов примыкающих к шарниру обнуляются, а на место элемента, соответствующего первому узлу, помещается Диагональный коэффициент этой же строки матрицы приравнивается единице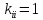, так, что для обусловленных перемещений уравнения принимают вид

,

где 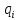- перемещение второго (третьего и т. д.) узла в шарнире,- перемещение первого узла в шарнире, уравнение которого не обнулялось и к которому отнесены все узловые силы, приложенные в шарнире по данному направлению:

for (int i = 0; i < f1.n; i++)

{

//Наложение главных граничных условий для подвижных соединений

if (Convert.ToInt32(f1.MatrCoor[i, 6]) > 0)

{

int sh = Convert.ToInt32(f1.MatrCoor[i, 6]) - 1;

for (int j = 0; j < f1.n * 3; j++)

{

K1[3 * sh, j] = K1[3 * sh, j] + K1[3 * i, j];

K1[3 * i, j] = 0;

}

P[3 * sh] = P[3 * i] + P[3 * sh];

P[3 * i] = 0;

K1[3 * i, 3 * sh] = -1.0;

K1[3 * i, 3 * i] = 1.0;

}

if (Convert.ToInt32(f1.MatrCoor[i, 7]) > 0)

{

int sh = Convert.ToInt32(f1.MatrCoor[i, 7]) - 1;

for (int j = 0; j < f1.n * 3; j++)

{

K1[3 * sh + 1, j] = K1[3 * sh + 1, j] + K1[3 * i + 1, j];

K1[3 * i + 1, j] = 0;

}

P[3 * sh + 1] = P[3 * i + 1] + P[3 * sh + 1];

P[3 * i + 1] = 0;

K1[3 * i + 1, 3 * sh + 1] = -1.0;

K1[3 * i + 1, 3 * i + 1] = 1.0;

}

if (Convert.ToInt32(f1.MatrCoor[i, 8]) > 0)

{

int sh = Convert.ToInt32(f1.MatrCoor[i, 8]) - 1;

for (int j = 0; j < f1.n * 3; j++)

{

K1[3 * sh + 2, j] = K1[3 * sh + 2, j] + K1[3 * i + 2, j];

K1[3 * i + 2, j] = 0;

}

P[3 * sh + 2] = P[3 * i + 2] + P[3 * sh + 2];

P[3 * i + 2] = 0;

K1[3 * i + 2, 3 * sh + 2] = -1.0;

K1[3 * i + 2, 3 * i + 2] = 1.0;

}

}

Решение системы уравнений и определение внутренних силовых факторов

Таким образом, уравнения равновесия для фермы примут вид

. (4.11)

Решение системы уравнений (4.8) сводится к вычислению вектора-столбца неизвестных перемещений

. (4.12)

Существуют стандартные программы решения системы линейных алгебраических уравнений методом Гаусса без нахождения обратной матрицы к матрице жесткости (SIMQ“Fortrun”).

После решения уравнений (4.11) и нахождения узловых обобщенных перемещений по выражению (4.12) определяются узловые перемещения в локальной системе координат для каждого элемента по соотношению (4.1):

(4.13)

По узловым обобщенным перемещениям можно найти величину относительной деформации, соответствующие нормальной силе , поперечной силе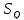и изгибающему моменту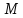(рис. 4.4):

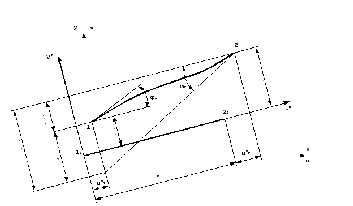
Рис. 4.4. Вычисление относительных деформаций

;

;

;

Данные соотношения позволяют найти внутренние силы в первом узле:

, (4.14)

где квадратная матрица есть часть локальной матрицы жесткости (левый верхний угол). Столбцы этой матрицы показывают внутренние силы в первом узле при единичном смещении в соответствующем направлении данного узла и жестком закреплении второго узла. Значения двух силовых факторов постоянны по длине элемен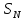та ,и равны в первом и втором узлах элемента.

В соответствии с правилом знаков, по которому при положительном изгибающем моменте растянуты нижние волокна

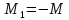
Изгибающий момент во втором узле определим из соотношения:

,

и линейного характера изменения изгибающего момент в пределах элемента:

(4.15)

На эпюре моментов ось направлена вниз относительно оси элемента

Для решения динамической задачи формируется система уравнений вида:

, (4.16)

в которой глобальная матрица масс формируется аналогично матрице жесткости путем сложения матриц масс элементов.

Поиск частного решения уравнения (4.16), при гармоническом внешнем воздействии 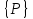, сводится к заданию выражения для обобщенных перемещенийв виде функций, подобных правой части уравнения.

Пусть внешние силы изменяются по закону:

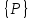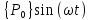=, (4.17)

тогда произвольное частное решение уравнения (4.16), соответствующее установившемуся режиму представим в виде

(4.18)

Вторая производная от выражения (4.18) равна

Подставляя выражение (4.15) в уравнение (4.13), получим

Приравнивая коэффициенты в левой и правой части при , приходим к линейной системе алгебраических уравнений:

,

вынесем за скобки неизвестные амплитудные значения

(4.19)

Обозначим

,

тогда уравнение (4.19) становится аналогичным (4.11)

(4.20)

В матрице и столбценеобходимо преобразовать строки, соответствующие перемещениям на которые наложены ограничения (необходимо учесть главные граничные условия), также как это производилось для матрицы [K] при статических расчетах. После система уравнений (4.20) решается с помощью программы, реализующей метод Гаусса, и находятся амплитуды вынужденных колебанийв решении (4.18) для установившегося режима.

По амплитудам , аналогично статическому решению вычисляют амплитуды внутренних силовых факторов по соотношениям (4.13), (4.14), (4.15).

Текст клиентского кода программы приведен в ПРИЛОЖЕНИИ 2.

Результаты расчетов представлены на рисунках 4.5, 4.6, 4.7,4.8.

Рис. 4.5 Координатная матрица узлов конструкции и схема расположения элементов.

Рис. 4.6 Топологическая матрица элементов конструкции и схема перемещение узлов при статической нагрузке.

Рис. 4.7. Матрица жесткости конструкции.

Рис. 4.8. Внутренние силовые факторы при статической нагрузке.

Метод конечных элементов для рамы является приближенным, поэтому точность расчетов, особенно при распределенных нагрузках (элемент №2), зависит от количества узловых точек и шаге разбиения на элементы. Так на участке №2 распределенные силы приводятся к узловым сосредоточенным силам и сосредоточенным парам сил, приложенным на границах элемента. Особенно влияние этих пар сил заметно на эпюре моментов вблизи шарниров, например, этим обусловлен скачёк в конце второго участка перед внутренним шарниром.

Также перераспределяются силы инерции при динамических расчетах в соответствии с коэффициентами матрицы масс. Для повышения точности вычислений целесообразно выполнить разбиение конструкции на большее число элементов, так система рис. 4.2 схема расположения узлов и элементов выглядит, как показано на рис. 4.9.

Рис. 4.9 Топологическая матрица элементов конструкции и схема перемещение узлов при статической нагрузке.

На рис.4.10 построены эпюры изгибающих моментов, из которых видно представление в виде ломаной линии на участках №4,5,6, которая заменяет параболу, получаемую при точном решении от действия распределенных сил.

Рис. 4.10. Внутренние силовые факторы, при статическом нагружении.

При тех же амплитудах нагрузки приложенных в динамике с частотой 1,5 рад/с получим амплитудные значения перемещений, представленные на рисунках 4.11.

Внутренние силовые факторы показаны на рисунке 4.12, из которых виден криволинейный характер эпюр изгибающих моментов на прямых участках конструкции, что обусловлено влиянием распределенных сил инерции.

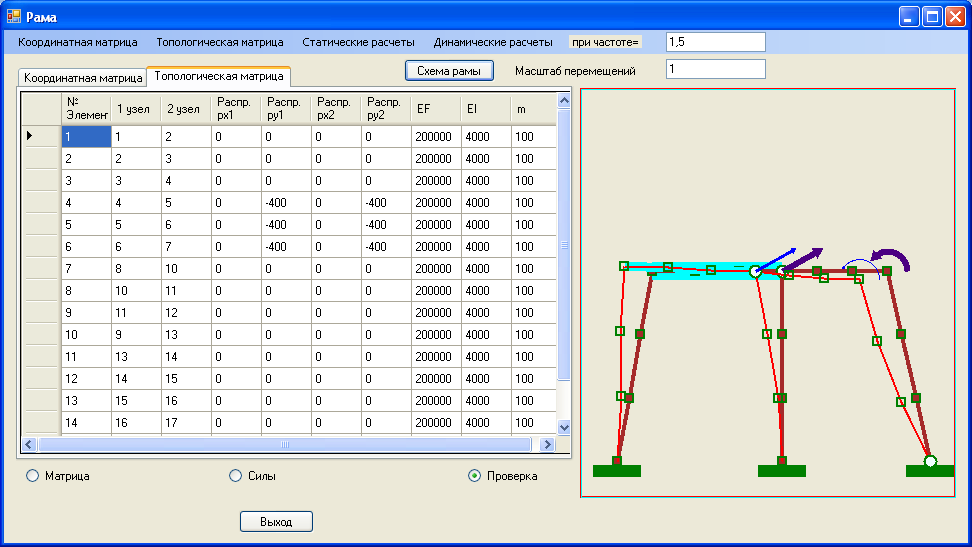
Рис. 4.11 Топологическая матрица элементов конструкции и амплитудные значения перемещений узлов при динамической нагрузке.

Рис. 4.12. Внутренние силовые факторы при динамическом нагружении.

5.Потенциальное течение несжимаемой жидкости

Потенциальное течение жидкости удовлетворяет условию неразрывности, которое запишется так:

.

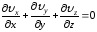То есть значения скоростей потока описываются уравнением для невязкой несжимаемой жидкости, для которого возможно записать уравнение Лапласа:

,

где - оператор Гамильтона,- потенциал скорости.

Это уравнение имеет вид:

. (5.1)

В рабочей зоне слой взвешенных частиц или пористого материала, или решетки создают дополнительное сопротивление движению жидкости (или воздуха при малых избыточных давлениях), и течение в этой зоне существенно отличается от остальной области.

Применяется допущение о том, что течение в слое твердых частиц подчинено закону Дарси, который описывает течение в пористых средах:

, (5.2)

где - коэффициент фильтрации, который является функцией плотности пористой среды и свойств потока жидкости. При ламинарном течении в порах существует соотношение для определения коэффициента:

, (5.3)

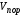где - пористость объема (,- объем пор;- полный объем);- безразмерный параметр;- средний диаметр пор;- плотность воздуха.

Таким образом, плоское течение в пористых средах описывается уравнением Лапласа вида

, (5.4)

где - коэффициенты фильтрации, которые могут быть различными в разных направлениях (например для моделирования решетки с жалюзи).

Течение в камере в целом может быть описано уравнением (5.4), если коэффициенты будут различными в разных областях течения. Функцияимеет физический смысл величины, пропорциональной избыточному статическому давлению в потоке, взятому с противоположным знаком. Граничные условия для уравнения (5.4) бывают двух типов:

а) главные граничные условия на (рис. 5.1) вида;

б) естественные граничные условия на с заданием нормальной составляющей скорости, где- нормаль к границе.

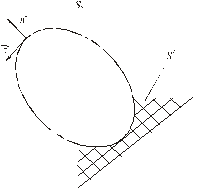
Рис. 5.1 Граничные условия в объеме воздуха: - поверхность с главными;- с естественными граничными условиями.

Метод конечных элементов в механике жидкости

В методе конечных элементов матрица для всей области течения формируется из матриц отдельных элементов, которые выражаются как функции узловых неизвестных. Последующий учет главных граничных условий приводит к изменениям общей матрицы. Аналогично величины, заданные в узлах элемента, образуют вектор обобщенной узловой нагрузки, разрешая полученную систему уравнений, определяют значения искомой функции в узлах.

Таким образом, основными этапами применения метода являются следующие:

1) дискретизация задачи, то есть представление области 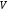в виде совокупности конечных элементов, взаимосвязанных в узловых точках;

2) получение матриц элементов;

3) построение общей матрицы для всей области и вектора нагрузки;

4) наложение граничных условий;

5) решение системы уравнений;

6) расчет любой другой функции, зависящей от узловых неизвестных.

Первый этап конечно-элементной процедуры состоит в разбиении области потока на ряд элементов. Затем каждый элемент рассматривается отдельно, и его свойства выводятся путем применения формулы метода Галеркина после выбора аппроксимирующих функций. Эти аппроксимирующие функции должны удовлетворять условиям допустимости и полноты для рассматриваемой задачи. Допустимость предполагает непрерывность искомой функции и ее производных между элементами, обеспечивающую корректность определения неизвестных в рамках вариационной формулировки. Условия полноты аппроксимирующих функций должны обеспечить стремление к постоянным производных при уменьшении размеров элемента.

После разбиения области на элементы характерные точки на границах элементов перенумеровывают и называют узлами.

Узлы выбирают в углах конечных элементов (рис. 5.2).

Таблица связности элементов имеет вид:

Таблица 5.1.

Матрица индексов (она же топологическая матрица)

№ элемента	Узел
1	1	2	3
2	2	4	3
3	3	4	5

Нумерация узлов проводится в одном и том же направлении, например, против хода часовой стрелки. Если аппроксимируется одна функция (потенциал скоростей), то полученная таблица является матрицей индексов решаемой задачи.

Рис. 5.2 Схема разбиения области на три треугольных конечных элемента

На рисунке 5.2 показаны глобальные номера узлов. Введем также локальную нумерацию, которая в таблице 5.1 соответствует буквам ,,(рис. 5.3).

Рис. 5.3. Локальные номера узлов

На втором этапе метода конечных элементов проводится аппроксимация неизвестной функции базисными функциями:

, (5.5)

где - номер узла в местной системе; для треугольного элемента с тремя узлами=3;

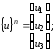(5.6)

.

Введем соответствующие матрицы конечных элементов для гармонического уравнения Лапласа (5.1) с граничными условиями обоих типов:

1) на;

2) на,

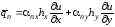где - направляющие косинусы нормали к.

Если выбранная аппроксимирующая функция удовлетворяет условию на, гдеможет быть частью внешней границы области, то воспользовавшись вариационной формулировкой метода Галеркина, можно записать:

.

Интегрируя это уравнение по частям, приходим к выражению

.

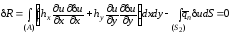Выражение в левой части есть вариация функционала

.

Закон изменения по полю конечного элемента аппроксимируем степенным полиномом вида

. (5.7)

Входящие в формулу неизвестные параметры можно выразить через узловые значения в узловых точках 1, 2, 3. Для угловых узлов получим

или в матричной форме

.

Отсюда

, (5.8)

иначе ,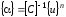

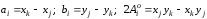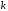где при=1, 2, 3;=2, 3, 1;=3, 1, 2;, причем- площадь элемента.

Используя зависимости (5.7) и (5.8), получим следующие выражения для производных функции :

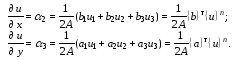(5.9)

и для производных от вариаций:

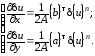(5.10)

Исключая из выражения (5.7) с помощью (5.9) параметры , находим

(5.11)

где

,

есть базисные функции для треугольного элемента. Подстановка выражений (5.9), (5.10), (5.11) в вариационную формулировку метода Галеркина дает

. (5.12)

После интегрирования левая часть уравнения (5.12) приводится к виду

(5.13)

Выражение (5.13) в компактной форме имеет вид:

, (5.14)

где - матрица коэффициентов влияния для треугольного элемента, состоящая в выражении (5.13) из двух слагаемых, стоящих в квадратных скобках.

Если коэффициенты фильтрации 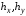различны (при наличии жалюзи и сеток) и местные оси координатне совпадают по направлению с глобальными осями координат, то матрицу коэффициентов влиянияможно вычислить в местной системе координат, а затем объединить с матрицами других элементов при сборке глобальной матрицы. При этом, кроме координат узлов элемента и коэффициентов, для таких элементов необходимо задать угол поворота локальных осей координат.

Правая часть равенства (5.12) существует только на части границы области. Предположим, что величинапостоянна, например, на стороне 2-3 (рис.5.3) Связь между координатамиитакова

.

Тогда для интеграла по в правой части (5.12) имеем:

. (5.15)

Из выражений (5.15), (5.13) по уравнению (5.12) следует

. (5.16)

Это алгебраическое уравнение связывает узловые значения искомой функции через матрицу коэффициентов влияния с потоком воздуха на границе области.

На третьем этапе конечно-элементной процедуры производят объединение матриц коэффициентов влияния 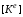для всей исследуемой области в матрицу. Размер этой матрицы определяется числом узловых неизвестных для всей области. Для области из трех элементов, показанной на рисунке 5.1 матрицабудет иметь размер 55.

Формирование ее проводят с помощью матрицы индексов (табл. 5.1). Организуется цикл по элементам (по строкам матрицы индексов), содержимое ячейки каждого элемента добавления в ячейкуглобальной матрицы коэффициентов влияния, причем номера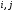берутся из строки матрицы индексов,- это локальные номера того же элемента.

Аналогично формируется глобальный вектор нагрузки .

Таким образом, система уравнений для области в целом имеет вид

, (5.17)

где 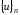- глобальные узловые неизвестные.

На четвертом этапе накладываются граничные условия. Эта операция выполняется для узловых переменных, в которых известны значения искомой функции.

Чтобы не изменять порядок системы уравнений (5.17) преобразуем матрицу и столбецполагая, что граничное условие первого типа задано в узле_:

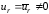
при 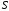=1, 2, …,

при ;

при

На пятом этапе решается система уравнений, например методом Гаусса. После решения системы уравнений (5.17), в которой учтены граничные условия, можно определить скорости потока

. (5.18)

С помощью приведенных отношений можно вычислить для всех элементов, причем в данном случае эти величины постоянны в пределах каждого из элементов. Если коэффициенты фильтрациизадавались в локальной системе отсчета, как и коэффициенты, то полученные скоростинеобходимо спроецировать на оси глобальной системы отсчета, используя матрицу поворота, состоящую из направляющих косинусов локальных осей.

По изложенному алгоритму составлены программы на алгоритмическом языке "C#", приведенные в ПРИЛОЖЕНИИ 3.

На рисунках 5.4, 5.5, 5.6, 5.7, 5.8. показан пример расчета потенциального течения несжимаемой жидкости на плоскости с графическим представлением исходных данных.

Рис. 5.4 Схема расположения узлов.

Рис. 5.5 Разбиение области течения на треугольные конечные элементы.

Рис. 5.6 Наложение граничных условий (скорости на границе отмечены на отрезках широкой сплошной линией – узлы 33-34; 1-2, заданные в координатной матрице потенциалы скоростей обозначены кругами в узлах 53, 55, 60, 61, 62 значение потенциала скоростей равно 10 в последнем столбце таблицы на рис. 5.4).

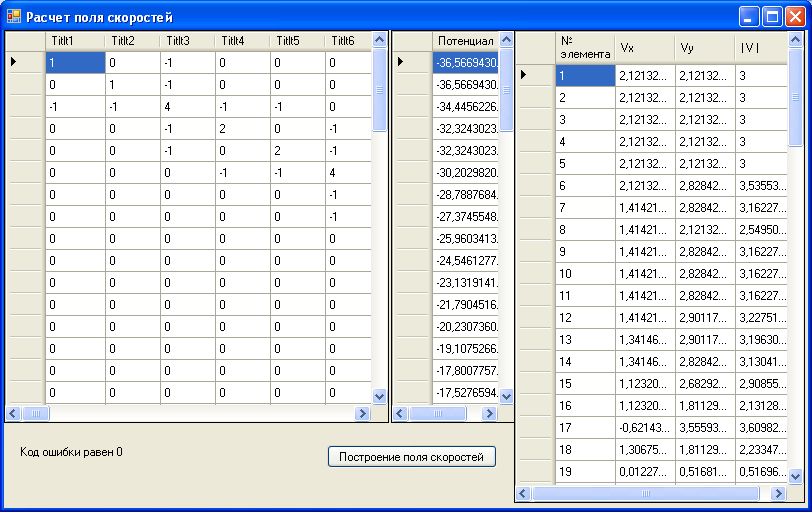
Рис. 5.7 Матрица коэффициентов влияния, значения потенциала скоростей в узлах и скорости в каждом конечном элементе.

Рис. 5.8 Распределение поля скоростей при плоском течении жидкости.