Измененные с троки матрицы жесткости при наложении граничных условий

	0	0	0	0	0	0	0	0	0	0	0
0		0	0	0	0	0	0	0	0	0	0
0	0	0	0	0	0		0	0	0	0	0
0	0	0	0	0	0	0		0	0	0	0
0	0	0	0	0	0	0	0	0	0		0
0	0	0	0	0	0	0	0	0	0	0

Не указанные элементы не изменяются.

Вектор-столбец нагрузки получит нулевые значения на закрепленных направлениях:

;

Если перемещения в закрепленных узлах не равны нулю, то их действительные значения, умноженные на диагональный элемент матрицы жесткости, помещают в соответствующую строку вектора нагрузки.

Решение системы уравнений и анализ результатов расчета

Таким образом, уравнения равновесия для фермы примут вид

. (2.8)

Решение системы уравнений (2.8) сводится к вычислению вектора-столбца неизвестных перемещений

. (2.9)

Существуют стандартные программы решения системы линейных алгебраических уравнений методом Гаусса без нахождения обратной матрицы к матрице жесткости (SIMQ“Fortrun”).

После решения уравнений (2.8) и нахождения узловых обобщенных перемещений по выражению (2.9) определяются узловые продольные перемещения в локальной системе координат для каждого элемента по формуле (2.1):

По продольным перемещениям в локальной системе координат можно найти величину относительной деформации :

(2.10)

И величину внутренних нормальных напряжений в каждом элементе

(2.11)

А также продольное внутреннее усилие

(2.12)

Для решения динамической задачи формируется система уравнений вида:

, (2.13)

в которой глобальная матрица масс формируется аналогично матрице жесткости путем сложения матриц масс элементов.

Поиск частного решения уравнения (2.13), при гармоническом внешнем воздействии , сводится к заданию выражения для обобщенных перемещенийв виде функций, подобных правой части уравнения.

Пусть внешние силы изменяются по закону:

=. (2.14)

Если ни одна из собственных частот колебаний не совпадает с частотой , то возможно найти амплитуды вынужденных установившихся колебаний.

Произвольное частное решение уравнения (2.13), соответствующее установившемуся режиму, представим в виде

(2.15)

Вторая производная от выражения (2.15) равна

Подставляя выражение (2.15) в уравнение (2.13), получим

Приравнивая коэффициенты в левой и правой части при , приходим к линейной системе алгебраических уравнений:

,

вынесем за скобки неизвестные амплитудные значения

(2.16)

Обозначим

,

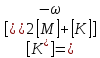тогда уравнение (2.16) становится аналогичным (2.8)

(2.17)

В матрице и столбце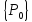необходимо преобразовать строки, соответствующие перемещениям, на которые наложены ограничения (необходимо учесть главные граничные условия), также как это производилось для матрицы [K] при статических расчетах. После система уравнений (2.17) решается с помощью программы, реализующей метод Гаусса и находятся амплитуды вынужденных колебанийв решении (2.15) для установившегося режима.

Разработка интерфейса пользователя

Исходные данные (Рис. 2.4) формируются в таблицах (элемент управления dataGridView) размещенных на вкладках (tabPage).

Рис. 2.4 Координатная матрица узлов конструкции.

С целью контроля корректности ввода данных, считываемые координаты узлов масштабируются и выводятся на форму в элементе PictureBoxи соединяются элементами в соответствии с топологической матрицей (Рис. 2.5). Здесь же отражаются условия закрепления конструкции и внешние узловые силы. После вычисления статических перемещений узлов или амплитудных значений обобщенных координат при решении динамической задачи, результаты в увеличенном масштабе наносятся на графическое представление фермы при нажатии кнопки «Построение».

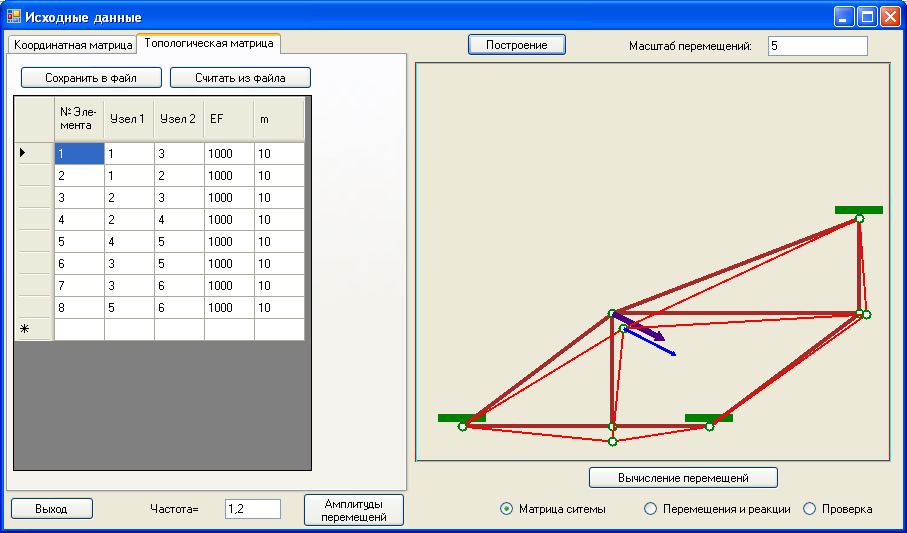
Рис. 2.5. Топологическая матрица элементов и изображение амплитуд перемещений в пятикратном увеличении.

Информация о числовых значениях всех матриц расчетных уравнений, которые формируются и преобразуются при проведении вычислений выводятся в таблице (dataGridView) на второй форме (Рис. 2.6), причем результат вывода зависит от радио-кнопок на основной форме. В зависимости от радио-кнопок и вида расчетов (статика, динамика) на второй форме в первой таблице отражаются: матрица жесткости системы, матрица системы уравнений для определения амплитуд установившихся колебаний при заданной частоте внешних сил, перемещения и реакции связей и статическая проверка решения.

Рис. 2.6. Результаты расчетов матриц системы и усилий в стержнях фермы.

Во второй таблице на форме 2 приводятся величины относительных деформаций и продольные усилия в стержнях конструкции. Текст клиентского кода программы приведен в ПРИЛОЖЕНИИ 1.

3. Формирование матриц жесткости и масс конечного элемента при исследовании деформации изгиба

Метод конечных элементов предусматривает задание форм перемещений не по всей длине стержня, а лишь на отдельных участках длины h(Рис. 3.1), на которые разбивается стержневая система:

Рис. 3.1. Выделение элемента длины h.

В пределах каждого участка для случая для случая изгиба стержня формы перемещений задаются кубическим полиномом:

(3.1)

Рис. 3.2. Нумерация перемещений в пределах элемента

Учитывая, что:

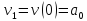
Если выразить 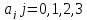через прогибы и углы поворота на краях рассматриваемого элемента, то получим:

Подставляя в выражение (3.1) имеем

Вынесем обобщенные координаты за скобки как общие множители и сформируем произведение матриц

, (3.2)

В компактной форме

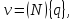
где q – вектор-столбец обобщенных перемещений, которыми являются перемещения узловых точек на границе элементов по ортогональным направлениям

- одномерные функции Эрмита:

Функции Эрмита удовлетворяют следующим условиям:

;;;

;;;

;;;

;;;

Каждая из функций Эрмита определяет изгиб жестко заделанной балки, которая получила единичное смещение по соответствующему направлению. Эти единичные смещения показаны на рисунке 3.3.

Выражения (3.2) можно представить в виде

;

Обозначим

Тогда

(3.3)

Рис. 3.3. Единичные смещения по обобщенным перемещениям

Равновесие элемента в обобщенных координатах имеет вид

где

- обобщенные силы от внутренних сил упругости элемента,

- обобщенные силы от внешних активных сил.

Чтобы получить обобщенные силы от внутренних сил упругости и матрицу жесткости для балочного элемента, запишем выражение потенциальной энергии внутренних сил элемента:

; (3.4)

где

(3.5)

E- модуль упругости материала балки,I- момент инерции сечения элемента.

Обобщенные силы от внутренних сил упругости выражаются через потенциальную энергию

Обозначим как матрицу жесткости элемента

После вычисления интеграла и подстановки матрицы получим

После перемножения матриц имеем:

(3.6)

Обобщенные силы от внутренних сил упругости примут вид

(3.7)

где – вектор-столбец обобщенных перемещений.

Обобщенные силы от внешних активных воздействий на элемент определим через возможную работу на обобщенных перемещениях

(3.8)

где в соответствии с (3.3) вариация поперечного перемещения

,

а проекция распределенной нагрузки на поперечное направление к оси элемента при линейном законе распределения выражается через ее узловые значения :

, (3.9)

при

,

.

(3.10)

где

,

Рис. 3.4. Интенсивность воздействия распределенных сил на рамный (балочный) конечный элемент

Тогда

. (3.11)

Коэффициенты в выражении возможной работы при соответствующих вариациях обобщенных координат 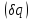называются обобщенными силами, то есть

(3.12)

где - значения распределенной нагрузки в узловых точках.

В выражение (3.12) необходимо добавить сосредоточенные узловые активные силы, в проекции на направление обобщенных перемещений.

Вернемся к условию равновесия в обобщенных координатах, представив его в виде

,

Тогда для конечного элемента оно выглядит так:

(3.13)

При решении динамической задачи уравнения составляем на основе уравнений Лагранжа второго рода:

(3.14)

где T – кинетическая энергия механической системы, которую необходимо выразить через обобщенные координаты:

,

где m –масса единицы длины стержневого элемента.

Выразим скорости точек элемента через обобщенные координаты и функции Эрмита, получим:

(3.15)

Под интегралом в выражении (3.15) стоит квадратная матрица:

После вычисления интеграла получаем выражение кинетической энергии через произведение обобщенных скоростей и матрицы масс [M] размером 44.

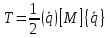, (3.16)

где

Вычисляя производные в левой части уравнений Лагранжа второго рода (3.14), получим:

и с учетом соотношения (3.7) запишем

(3.17)

Уравнение (3.17) определяет модель движения упругой динамической системы под действием внешних переменных сил.

Формирование матриц жесткости и масс рамного конечного элемента

Рамный конечный элемент плоской конструкции кроме деформаций изгиба испытывает деформации растяжения-сжатия и отличается от элемента балки, тем что к четырем обобщенным перемещениям добавляются два, аналогичные обобщенным перемещениям элемента фермы(Рис. 1.2). Перенумеруем обобщенные перемещения элемента в порядке следования узлов (рис. 3.5).

Рис. 3.5. Нумерация перемещений в пределах элемента

Что будет соответствовать вектор-столбцу перемещений узлов элемента

.

Тогда к внутренним силам добавится продольная сила и ее учет в матрице жесткости приведет к ячейкам, аналогичным ячейкам матрицы ферменного элемента

(3.18)

Подобным образом расширяется матрица масс в уравнении (3.17):

; (19)

И вектор-столбец внешних узловых сил :

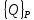(3.20)

После формирования всех матриц для исследования динамического равновесия каждого элемента можно записать уравнения вида (3.17), если в правую часть добавить сосредоточенные внешние силы, приложенные в узлах элемента

(3.21)

в которых размерность системы равна шести. Это уравнение составлено в локальной системе координат (рис. 3.5).