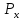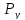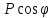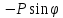МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Вятский государственный университет»

Факультет строительства и архитектуры

Кафедра теоретической и строительной механики

А.В. Алёшкин

Алгоритмическое программирование в задачах механики

Учебное пособие по дисциплине

"Численные методы и алгоритмы решения инженерных задач"

Для специальностей факультета строительства и архитектуры

всех форм обучения

Киров 2014

Содержание

Введение…………………………………………………………………….3

1. Основные положения метода конечных элементов

в механике упругого тела на примере плоской

фермы………………………………………………………………………4

2. Формирование матриц жесткости и масс в глобальной

системе координат для фермы…………………………………………10

3. Формирование матриц жесткости и масс конечного

элемента при исследовании деформации изгиба…………………..21

4. Формирование матриц жесткости и масс в глобальной

системе координат для рамы…………………………………………..31

5. Потенциальное течение несжимаемой жидкости…………………48

6. Задания для выполнения лабораторных работ…………………..58

Литература………………………………………………………………...89

ПРИЛОЖЕНИЯ…………………………………………………………..90

Введение

Учебное пособие по курсу «Численные методы и алгоритмы решения инженерных задач» содержит теоретические основы применения метода конечных элементов к решению прикладных задач механики стержневых систем, работающих на растяжение и изгиб, а также к исследованию потенциальных течений несжимаемой жидкости.

В качестве базового инструмента в приведенных примерах используется среда разработки MicrosoftVisualstudio.

С целью освоения навыков алгоритмического программирования задач механики приводятся ссылки на фрагменты кода на языке C#, которые реализуют математические матричные соотношения МКЭ в последовательность вычислительных операций и графическую интерпретацию полученных результатов (ПРИЛОЖЕНИЯ).

Предполагается наличие у читателя начальных знаний по объектно-ориентированному программированию [1,2,3], созданию графического интерфейса для Windows-приложений [4,5], а также прохождение курсов теоретической механики [6], сопротивления материалов и математического моделирования [7,8,9].

Пособие содержит задания для выполнения лабораторных работ, которые усложняются по мере освоения курса и служат для последовательного приобретения навыков расчета равновесия и движения абсолютно твердого тела, затем системы тел испытывающих деформацию растяжения-сжатия, затем и деформацию изгиба. Последнее задание посвящено расчету потенциального течения, которое применимо к движению невязкой жидкости и к воздушному потоку при невысоких давлениях, например в системах вентиляции и пневмосепарации.

Варианты заданий по каждой теме студентами заочной формы обучения выбираются по последней цифре зачетной книжки. Если эта цифра «0», то номер варианта «10». Студентам очного отделения номер варианта сообщает преподаватель на текущей лабораторной работе.

1. Основные положения метода конечных элементов в механике упругого тела на примере плоской фермы

Метод конечных элементов основан на мысленном представлении сплошного тела в виде совокупности отдельных элементов, взаимодействующих между собой в конечном числе узловых точек (Рис.1.1). В этих точках прикладываются некоторые фиктивные усилия взаимодействия, характеризующие действие распределенных внутренних напряжений вдоль реальных границ стыков смежных элементов. Проблема определения напряженно-деформированного состояния сводится к расчету упругой системы с конечным числом степеней свободы.

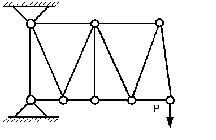
Рис. 1.1 Стержневая механическая система.

Замена исходной физической системы совокупностью дискретных элементов подразумевает равенство энергий физической системы и ее дискретной модели. Характер взаимодействия между элементами должен быть таким, чтобы уменьшение размеров конечных элементов привело к получению решения, стремящегося к точному, если погрешность вычислений, связанная с увеличением размерности системы разрешающих уравнений, остается малой.

В пределах каждого конечного элемента перемещения аппроксимируются некоторыми функциями, которые должны удовлетворять следующим условиям:

- на границах между конечными элементами должны выполняться условия совместимости перемещений;

- в узлах конечных элементов эти функции должны давать перемещения, равные узловым перемещениям.

При решении статической задачи полная потенциальная энергия Псистемы, находящейся в равновесии, имеет минимум. Использование вариационного уравнения Лагранжа

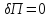(1.1)

дает уравнения равновесия для внешних и внутренних сил. Потенциальная энергия может быть представлена как функция узловых перемещений, поэтому уравнения равновесия, полученные по уравнению (1.1), связывают приведенные к узловым перемещениям внешние и внутренние силы

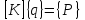, (1.2)

где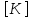- матрица жесткости механической системы;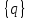- узловые перемещения (обобщенные координаты); {P}- вектор-столбец внешних узловых сил.

При решении динамической задачи, кроме потенциальной энергии Пнеобходимо учесть кинетическую энергию системыT.

На основании общего уравнения динамики

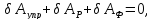
где 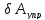- возможная работа упругих сил;- возможная работа внешних сил системы;- возможная работа сил инерции.

Если выбрать в качестве обобщенных координат узловые перемещения, то для голономной системы в соответствии с уравнениями Лагранжа второго рода можно записать

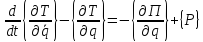(1.3)

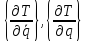где - вектор-столбцы соответственно частных производных от кинетической энергии по обобщенным скоростям и координатам;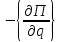- обобщенные потенциальные силы;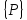- вектор столбец обобщенных активных сил. Для линейно-упругих систем уравнение (1.3) преобразуется к виду:

, (1.4)

где 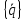- вектор столбец обобщенных ускорений;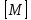- матрица масс системы, приведенных к узловым перемещениям. Матрицы масс и жесткостей определяются из выражений кинетической и потенциальной энергий системы соответственно

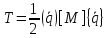; (1.5)

. (1.6)

В случае малой упругой деформации элементы этих матриц считаются постоянными коэффициентами. Общая матрица составляется с помощью матриц жесткости каждого из элементов.

Формирование матриц жесткости и масс ферменного конечного элемента

Ферменный конечный элемент применяется для моделирования прямолинейных стержней конструкции, работающих на растяжение-сжатие (рис.1.2).

Рис. 1.2. Конечный элемент фермы: 1; 2 - локальные номера узлов; x- локальная ось,u₁,u₂- узловые перемещения в локальной системе координат.

В пределах каждого участка для случая для случая растяжения стержня формы перемещений задаются линейным полиномом:

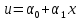(1.7)

Постоянные 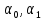определяются из условий:

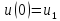
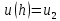
На основе выражения (1.7) получим два уравнения для нахождения 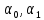через узловые перемещения:

,

;

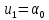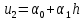Из которых определяем

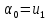
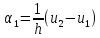
Тогда выражение (1.7) примет вид

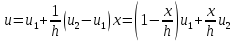
или в матричном представлении

(1.8)

где 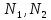функции Эрмита, отражающие форму перемещений в пределах конечного элемента:

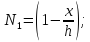
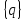-обобщенные координаты конечного элемента

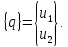
Равновесие элемента в обобщенных координатах имеет вид

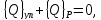
где

- обобщенные силы от внутренних сил упругости элемента,

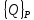- обобщенные силы от внешних активных сил.

Чтобы получить обобщенные силы от внутренних сил упругости и матрицу жесткости для ферменного элемента, запишем выражение потенциальной энергии внутренних сил элемента:

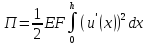; (1.9)

где

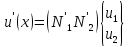(1.10)

причем

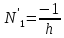
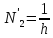
E- модуль упругости материала фермы,F-площадь поперечного сечения элемента.

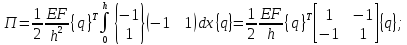
Обобщенные силы от внутренних сил упругости выражаются через потенциальную энергию

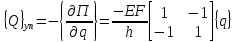(1.11)

Обозначим как матрицу жесткости элемента

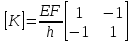. (1.12)

Обобщенные силы от внутренних сил упругости примут вид

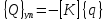(1.13)

где 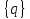– вектор-столбец обобщенных перемещений.

Обобщенные силы от внешних активных воздействий на элемент определим через возможную работу на обобщенных перемещениях

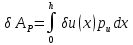(1.14)

где в соответствии с (8) вариация продольного перемещения

,

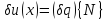а проекция распределенной нагрузки на продольное направление оси элемента при линейном законе распределения выражается через ее узловые значения :

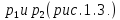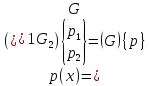, (1.15)

Рис. 1.3. Продольные распределенные внешние силы в элементе

При линейном законе распределения нагрузки

,

.

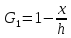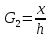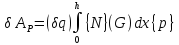(1.16)

где интеграл равен

,

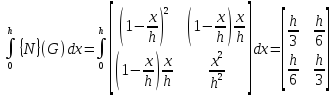Тогда

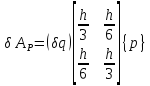. (1.17)

Коэффициенты в выражении возможной работы при соответствующих вариациях обобщенных координат 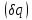называются обобщенными силами, то есть

(1.18)

где 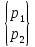- значения распределенной нагрузки в узловых точках.

В выражение (1.18) необходимо добавить сосредоточенные узловые активные силы, в проекции на направление обобщенных перемещений. Именно узловые силы как правило задаются для задачи о равновесии фермы.

Вернемся к условию равновесия в обобщенных координатах, представив его в виде

,

Тогда для конечного элемента оно выглядит так:

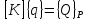(1.19)

При решении динамической задачи уравнения составляем на основе уравнений Лагранжа второго рода:

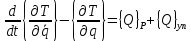(1.20)

где T – кинетическая энергия механической системы, которую необходимо выразить через обобщенные координаты:

,

где m –масса единицы длины стержневого элемента.

Выразим скорости точек элемента через обобщенные координаты и функции Эрмита, получим:

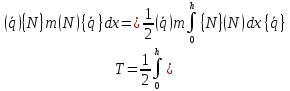(1.21)

Под интегралом в выражении (1.21) стоит квадратная матрица:

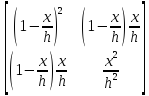
После вычисления интеграла получаем выражение кинетической энергии через произведение обобщенных скоростей и матрицы масс [M] размером 2.

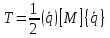, (1.22)

где

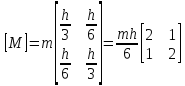(1.23)

Вычисляя производные в левой части уравнений Лагранжа второго рода (1.20), получим:

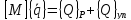
и с учетом соотношения (1.13) запишем

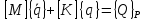(1.24)

Уравнение (1.24) определяет модель движения упругой динамической системы под действием внешних переменных сил.

2. Формирование матриц жесткости и масс в глобальной системе координат для фермы

Узловые перемещения ферменного конечного элемента в локальной системе координат 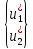выражаются через глобальные узловые обобщенные перемещения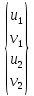и углы α и β рис.2.1 в виде

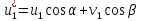
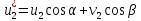
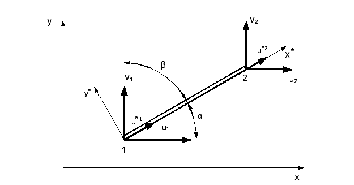
Рис. 2.1. Преобразование на плоскости узловых перемещений ферменного конечного элемента

В матричной форме это преобразование запишем так

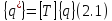
где

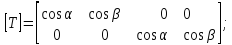(2.2)

;

.

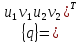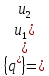Направляющие косинусы локальной оси 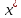определяются глобальными координатами узлов

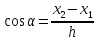, (2.3)

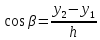, (2.4)

где

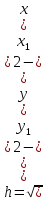(2.5)

длина элемента.

Матрица жесткости конечного элемента в глобальной системе координат преобразуется с учетом выражения (2.1) и зависимости для потенциальной энергии элемента, которая не зависит от выбора системы отсчета:

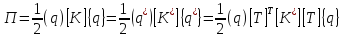
тогда

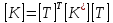(2.6)

Аналогично преобразуется и матрица масс конечного элемента , на основании того, что кинетическая энергия элемента не зависит от направления осей координат, по аналогии с потенциальной энергией получим:

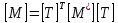(2.7)

Узловые силы приложены к узлам фермы и задаются в глобальной системе координат, поэтому в преобразованиях не нуждаются.

Рассмотрим, как формируется матрица жесткости и уравнения равновесия для механической системы, содержащей ферменные конечные элементы (рис. 2.2), к которой приложена сила P=300 кН. Известны размеры

Без учета закрепления узлов необходимо ввести 12 обобщенных перемещений (по два на каждый из шести узлов). Матрица жесткости для такой системы будет иметь размер 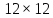, а матрица каждого элемента, приведенная к глобальной системе координат, имеет размерТаким образом, конечные элементы, узлы которых совпадают должны вносить общий суммарный вклад в соответствующие элементы матрицы жесткости.

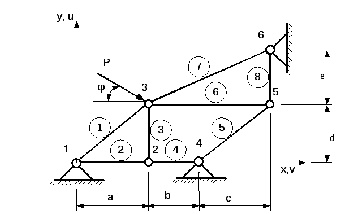
Рис. 2.2 Ферма с номерами узлов: 1...6 и номерами стержней 1...8 (в окружностях)

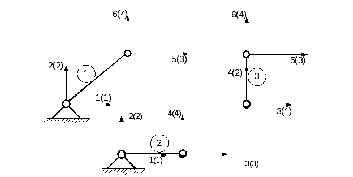
Рис. 2.3 Нумерация глобальных обобщенных координат для трех первых элементов с указанием в скобках номеров внутри элемента

Если условно обозначить матрицу жесткости первого элемента:

;

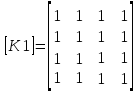второго элемента:

;

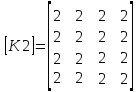третьего элемента:

;

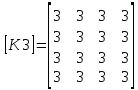то левый верхний угол общей матрицы жесткости без учета вклада других элементов примет вид

[K]=

2+1	2+1	2	2	1	1
2+1	2+1	2	2	1	1
2	2	2+3	2+3	3	3
2	2	2+3	2+3	3	3	...
1	1	3	3	3+1	3+1
1	1	3	3	3+1	3+1
		...

В качестве исходных данных для формирования матрицы жесткости потребуется координатная матрица для узлов и топологическая матрица для конечных элементов. Координатная матрица – это таблица, которая содержит информацию о номере узла и его координатах, а также о способе его закрепления и приложенных сосредоточенных силах. В соответствии с количеством узлов выбирается число обобщенных перемещений. Для конструкции рисунка 2.2 с учетом размеров координатная матрица имеет вид таблицы 2.1.

Таблица 2.1

Координатная матрица

№ узла	x	y			Закрепление по x	Закрепление по y
1	0	0	0	0	1	1
2	2	0	0	0	0	0
3	2	1,8			0	0
4	3,3	0	0	0	1	1
5	5,3	1,8	0	0	0	0
6	5,3	3,3	0	0	1	1

В последних двух столбцах 0 – соответствует свободному узлу, а 1 - закрепленному, в соответствии с направлением оси.

Топологическая матрица содержит информацию об элементах конструкции и представляет собой таблицу, столбцы которой соответствуют локальным номерам узлов начала и конца элемента, а строки номеру элемента. Внутренние ячейки таблицы содержат глобальные номера узлов, соответствующие каждому элементу, кроме этой информации в каждую строку добавляем характеристики прочностных и массовых свойств элементов. Для конструкции рисунка 2.2 топологическая матрица примет вид таблицы 2.2.

Таблица 2.2