
- •Интегральное исчисление
- •Неопределенный интеграл
- •Свойства неопределенного интеграла
- •Основные методы интегрирования
- •Интегрирование рациональных дробей
- •Интегрирование тригонометрических функций
- •Интегрирование некоторых иррациональных функций
- •Определенный интеграл
- •Свойства определенного интеграла
- •2.2 Интегрирование методом замены переменной и по частям в определенном интеграле
- •Несобственные интегралы с бесконечными пределами
- •Геометрические и физические приложения определенного интеграла
- •Контрольные вопросы и задания
Интегрирование тригонометрических функций
Рассмотрим
нахождение интегралов вида
![]() .
.
В зависимости от степени тригонометрических функций используются следующие приемы:
если
 – целое положительноенечетное
число
– целое положительноенечетное
число
 ,
то, отделяя от нечетной степени один
сомножитель
,
то, отделяя от нечетной степени один
сомножитель ,
выражаем с помощью основного
тригонометрического тождества
,
выражаем с помощью основного
тригонометрического тождества оставшуюся четную степень
оставшуюся четную степень и делаем подстановку
и делаем подстановку ,
тогда
,
тогда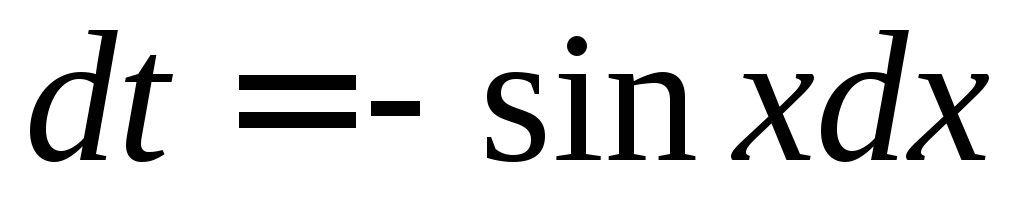 и
и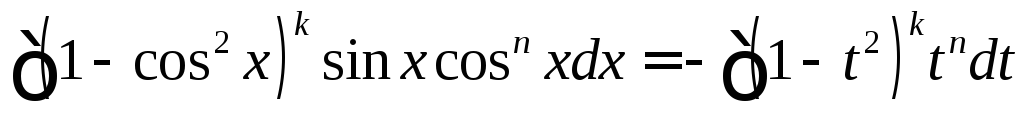 сводится к табличным интегралам.
сводится к табличным интегралам.
Пример 1. Найти
интеграл
![]() .
.
Здесь
![]() – нечетное число, тогда преобразуем
подынтегральную функцию и сделаем
подстановку
– нечетное число, тогда преобразуем
подынтегральную функцию и сделаем
подстановку![]() :
:

![]() .
.
если
 – целое положительноенечетное
число
– целое положительноенечетное
число
 ,
то, отделяя от нечетной степени один
сомножитель
,
то, отделяя от нечетной степени один
сомножитель ,
выражаем с помощью основного
тригонометрического тождества
,
выражаем с помощью основного
тригонометрического тождества оставшуюся четную степень
оставшуюся четную степень и делаем подстановку
и делаем подстановку ,
тогда
,
тогда и
и сводится к табличным интегралам.
сводится к табличным интегралам.
Пример 2.
Найти интеграл
![]() .
.
Здесь
![]() – нечетное число, тогда преобразуем
подынтегральную функцию и сделаем
подстановку
– нечетное число, тогда преобразуем
подынтегральную функцию и сделаем
подстановку![]() :
:

 .
.
Пример 3. Найти
интеграл
![]() .
.
![]()
![]() .
.
если
 и
и – целые неотрицательныечетные
числа, то используем формулы
понижения степени:
– целые неотрицательныечетные
числа, то используем формулы
понижения степени:
![]() .
.
Пример 4.
Найти интеграл
![]() .
.
Здесь
![]() – четные числа. Тогда
– четные числа. Тогда

 .
.
Для интегрирования произведений синусов и косинусов различных аргументов применяются тригонометрические формулы преобразования произведений в суммы или разности.
Пример 5. Найти
интеграл
![]() .
.
![]()
![]() .
.
Интегрирование некоторых иррациональных функций
Интегралы вида
 ,
т.е. интегралы, содержащие квадратичную
иррациональность в знаменателе. Для
их нахождения надо под корнем выделить
полный квадрат и сделать подстановку
,
т.е. интегралы, содержащие квадратичную
иррациональность в знаменателе. Для
их нахождения надо под корнем выделить
полный квадрат и сделать подстановку .
.
Пример 1. Найти
интеграл
 .
.

 .
.
Если подынтегральное выражение содержит корни от линейной функции
 ,
т.е.
,
т.е. и
т.д., то интеграл от иррациональной
функции находится с помощью подстановки
и
т.д., то интеграл от иррациональной
функции находится с помощью подстановки ,
где
,
где – наименьшее общее кратное чисел
– наименьшее общее кратное чисел (обозначается
(обозначается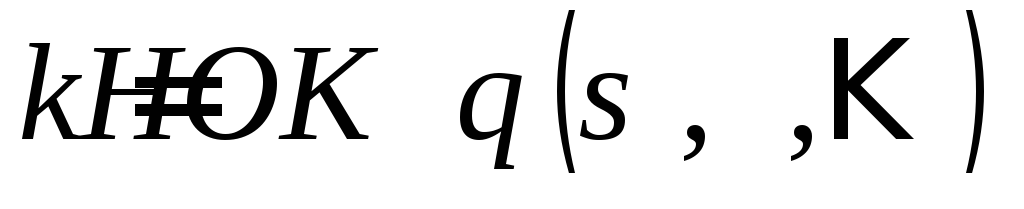 ).
).
Пример 2. Найти
интеграл
![]() .
.
Пусть
![]() .
Тогда
.
Тогда
![]()
![]() .
.
Пример 3. Найти
интеграл
 .
.
Здесь
![]() .
Пусть
.
Пусть![]() и
и

 .
.
Замечание. Рассмотренные методы интегрирования позволяют во многих случаях найти первообразную подынтегральной функции (неопределенный интеграл). Однако первообразная не всякой элементарной функции является элементарной функцией. В этом случае говорят о неберущихся интегралах.
Например,
не существует элементарной функции,
производная которой равна
![]() ,
т.е.
,
т.е.![]() – неберущийся интеграл. Аналогично,
– неберущийся интеграл. Аналогично,![]() – примеры неберущихся интегралов.
Первообразные для таких интегралов
существуют и являются специальными
функциями.
– примеры неберущихся интегралов.
Первообразные для таких интегралов
существуют и являются специальными
функциями.
Определенный интеграл
Пусть функция
![]() определена на отрезке
определена на отрезке![]() .
Разобьем отрезок
.
Разобьем отрезок![]() на
на![]() частичных отрезков
частичных отрезков![]() точками
точками![]() .
.
Интегральной
суммой функции
называется сумма
 ,
где
,
где![]() – длина
– длина![]() -
го частичного отрезка разбиения,
-
го частичного отрезка разбиения,![]() – произвольная точка отрезка.
– произвольная точка отрезка.
Геометрически
![]() представляет собой алгебраическую
сумму площадей прямоугольников с
основаниями
представляет собой алгебраическую
сумму площадей прямоугольников с
основаниями![]() и высотами
и высотами![]() .
.
Определенным
интегралом или
интегралом
Римана от
функции
![]() называется конечный предел
называется конечный предел![]() при
при![]() ,
т.е.
,
т.е. ,
не зависящий от способа разбиения
отрезка на части и от выбора точек
,
не зависящий от способа разбиения
отрезка на части и от выбора точек![]() (если он существует).
(если он существует).
В этом случае
функция
![]() называетсяинтегрируемой
на отрезке
называетсяинтегрируемой
на отрезке
![]() .
.
Определенный
интеграл от функции
![]() на отрезке
на отрезке![]() обозначается
обозначается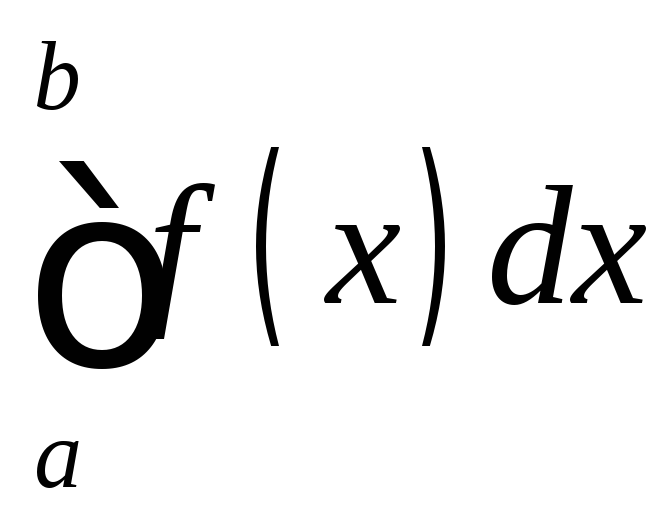 ,
где
,
где![]() – нижний предел интегрирования,
– нижний предел интегрирования,![]() – верхний предел интегрирования.
– верхний предел интегрирования.
Таким образом, по определению
 .
(*)
.
(*)
Геометрически
определенный интеграл представляет
собой алгебраическую сумму площадей
фигур, ограниченных графиком функции
![]() ,
осью
,
осью![]() и прямыми
и прямыми![]() ,
причем площади, расположенные выше оси
,
причем площади, расположенные выше оси![]() ,
входят в эту сумму со знаком плюс, а
площади, расположенные ниже оси
,
входят в эту сумму со знаком плюс, а
площади, расположенные ниже оси![]() ,
– со знаком минус.
,
– со знаком минус.
Теорема. Если функция непрерывна на отрезке, то она интегрируема на нем.
Нахождение определенного интеграла по определению довольно затруднительно, поэтому при вычислении определенного интеграла от непрерывной функции используют формулу Ньютона – Лейбница:
 ,
(3)
,
(3)
где
![]() – первообразная функции
– первообразная функции![]() на отрезке
на отрезке![]() .
.
Формула (3) устанавливает связь определенного интеграла с неопределенным интегралом и позволяет вычислить определенный интеграл, если известна одна из первообразных подынтегральной функции.
Примеры:
 .
. .
.
