ГОУ ВПО

"Российский Экономический университет имени Г.В.Плеханова"

Кафедра

"Математические методы в экономике"

Контрольная работа №3

по дисциплине

"Эконометрика"

Выполнила:

студентка финансового факультета

гр. 2312

Макаревич А.В.

Проверил:

Колпаков В. Ф.

Москва – 2010

Задача 3. По территориям региона приведены данные в таблице.

Задание.

1. Постройте корреляционное поле и по его виду определите форму зависимости между Х и Y.

2. Оцените по МНК параметры уравнения линейной регрессии.

3. Оцените выборочный коэффициент корреляции и сделайте предварительный вывод о силе линейной взаимосвязи параметров Х и Y.

4. Проверьте качество уравнения регрессии:

   1. значимость коэффициентов регрессии;

   2. интервальные оценки коэффициентов регрессии;

   3. значимость уравнения регрессии в целом.

5. Проинтерпретируйте результаты.

6. Сделайте прогноз среднедневной заработной платы и доверительный интервал для нее при значении Х = Х_прогн..

Вариант 3.5

Номер региона	Среднедушевой прожиточный минимум в день одного трудоспособного, руб., Х	Среднедневная заработная плата, руб., Y
1	310	800
2	430	920
3	525	1000
Номер региона	Среднедушевой прожиточный минимум в день одного трудоспособного, руб., Х	Среднедневная заработная плата, руб., Y
4	350	850
5	618	1090
6	785	1120
7	815	1240
8	595	1080
9	490	1000
10	700	1150

Х_прогн= 820; Уровень значимости = 0,07.

В целях нормирования расходования средств необходимо подобрать наиболее адекватную статистическим данным экономико-математическую модель из следующих функций:

1. Линейной;

2. Полином 2-го порядка;

3. Степенной;

4. Показательной;

5. Равносторонней гиперболы;

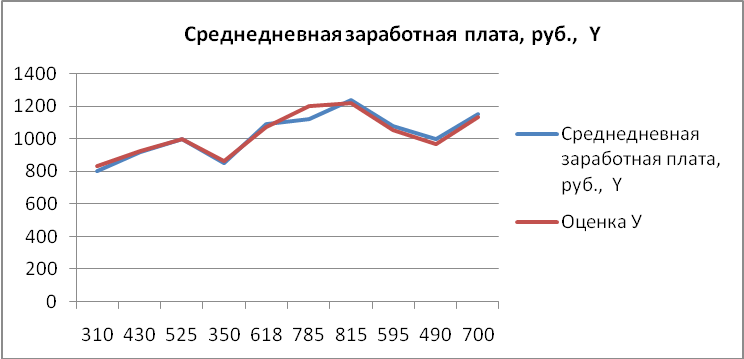
Результаты решения этой задачи с использованием ППП Excel представлены ниже:

1. Для начала воспользуемся данными, полученными по работе с парной регрессией

Номер региона	Среднедушевой прожиточный минимум в день одного трудоспособного, руб., Х	Среднедневная заработная плата, руб., Y	Оценка У	Ошибки Е
1	310	800	829,9853618	-29,98536178
2	430	920	922,9232354	-2,923235433
3	525	1000	996,4990521	3,500947921
4	350	850	860,964653	-10,964653
5	618	1090	1068,525904	21,47409584
6	785	1120	1197,864445	-77,864445
7	815	1240	1221,098913	18,90108658
8	595	1080	1050,712812	29,28718829
9	490	1000	969,3921723	30,60782774
10	700	1150	1132,033451	17,96654884

Tb1	Tb0	R^2
11,348546	14,76842676	0,941515977
F	A%	V%
128,7894957	2,348739953	3,455983531

0,77448228	589,8958548
0,068245067	39,9430396
0,941515977	35,4238312
128,7894957	8
161611,2175	10038,78253