Лекции Матан / Глава 5. Числовые ряды
.docГлава V: Числовые ряды
п. 1 Определения и примеры
Нам уже приходилось сталкиваться с суммами, содержащими бесконечное число слагаемых. Например, бесконечные десятичные периодические дроби
,
бесконечно убывающая геометрическая прогрессия
.
Многие числа могут быть записаны в виде таких сумм, с помощью которых их приближенное значение вычисляется с нужной точностью.
Например,
,
,
,
.
Определение 1
Пусть
- числовая последовательность. Тогда
выражение вида
называют
числовым
рядом. При
этом
называют
общим членом
ряда
.
Замечание 1
Что понимать под суммой бесконечного числа слагаемых? Единого правила нет. Наиболее употребительна интерпретация Коши или суммирование по Коши
Определение 2
Конечная сумма
первых
членов ряда
называется n-ой
частичной суммой
данного ряда.
Заметим, что изучение числовых рядов есть новая форма изучения числовых последовательностей, так как:
1) каждому данному
ряду однозначно соответствует
последовательность частичных сумм
;
2) каждой данной
последовательности
однозначно соответствует ряд, для
которого эта последовательность является
последовательностью его частичных сумм
(достаточно положить
при
).
Определение 3:
Говорят, что ряд
сходится,
если сходится последовательность
его частичных сумм. Тогда число
,
если существует этот предел, называется
суммой ряда
.
В противном
случае, когда предел
не существует или последовательность
является неограниченной, говорят, что
ряд
расходится.
Пример 1
Рассмотрим ряд:
.
Учитывая,
что
,
получим
Тогда
.
Это означает, что исходный ряд сходится,
и его сумма равна
.
Пример 2
Рассмотрим ряд, составленный из членов геометрической прогрессии:
.
Его
частичная сумма при
имеет вид:
.
Очевидно,
что при
последовательность
сходится и имеет предел, равный
.
Тогда ряд сходится и имеет сумму
.
При
последовательность
неограниченна, следовательно, исходный
ряд расходится.
Пример 3
Рассмотрим
ряд:
.
Поскольку последовательность его
частичных сумм
не имеет предела, то ряд расходится.
Так как вопрос о сходимости ряда по определению эквивалентен вопросу о сходимости последовательности его частичных сумм, то необходимое и достаточное условие сходимости данного ряда вытекает из критерия Коши сходимости последовательности частичных сумм этого ряда (принцип согласованности).
Теорема 1 Критерий Коши
Для того, чтобы
ряд
сходился, необходимо и достаточно,
чтобы:
,
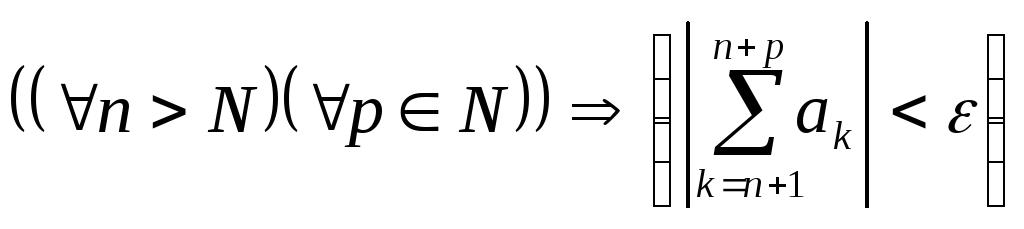т.е. сколь угодно длинные куски сходящегося
ряда могут быть сколь угодно малыми по
модулю, если их взять достаточно далеко.
Доказательство:
Для доказательства
этой теоремы достаточно заметить, что
и воспользоваться принципом полноты.
Следствие 1 Необходимый признак сходимости ряда
Если ряд
сходится, то
.
Доказательство:
Пусть ряд
сходится. Тогда в силу критерия Коши
.
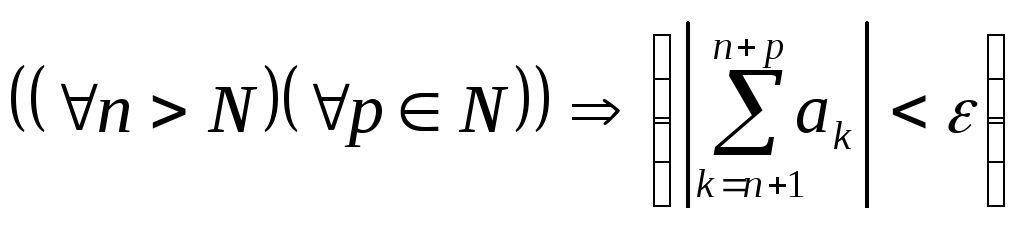Положим
.
Тогда
.
Если
,
то (
(
))
.
Замечание 2
Обратное утверждение,
вообще говоря, неверно. Стремление к
нулю
-го
члена ряда при
является лишь необходимым условием
сходимости ряда, т.е. это означает, что
если
при
не стремится к нулю, то ряд расходится.
Пример 4:
Рассмотрим
ряд:
,
который называют гармоническим.
Очевидно, что выполнено необходимое
условие сходимости -
.
Покажем, что ряд сходится. Для этого
воспользуемся критерием Коши. Докажем,
что для
не существует такого номера
,
что при
для любого натурального
выполняется условие
.
В
самом деле, если взять
,
то для сколь угодно большого
:
.
В силу критерия Коши ряд расходится.
п.2 Общие свойства сходящихся рядов
Определение 1
Любой
ряд
можно представить в виде
,
где
- главная часть ряда (голова), а
-
-й
остаток ряда (хвост).
Теорема 1
Ряд
ведет себя так же, как ведет себя его
остаток.
Доказательство:
Пусть ряд
сходится, т.е.
.
Тогда
,
где
- конечная сумма первых
членов ряда. Переходя к пределу при
фиксированном
и
,
получим, что если ряд
сходится, то и значение
должно быть конечно, т.е. ряд
сходится, и наоборот, если
сходится, то значение
конечное, т.е. и
конечное, т.е. ряд
сходится. Если же значение
не существует или ограниченно, то и
должно быть таким же.
Теорема 2 Ассоциативность
Пусть
ряд
сходится. Тогда, не нарушая порядка
следования его членов, их можно
сгруппировать (произвольным образом
расставить скобки) так, что ряд,
составленный из групп, будет сходиться
к той же сумме, что и исходный ряд.
Доказательство:
Сгруппируем члены ряда следующим образом
,
где
,
…. Составим последовательность частичных
сумм
,
,
…,
,
,
…, которая является подпоследовательностью
последовательности частичных сумм ряда
.
Следует заметить, что для исследования числовых рядов на сходимость достаточно результатов теории числовых последовательностей. Однако эти методы громоздки и чрезвычайно неудобны. Поэтому изучим другие методы исследования сходимости числовых рядов. Для этого удобно рассмотреть отдельно знакопостоянные и знакопеременные ряды. Все признаки сходимости числовых рядов подразделяются на внутренние, когда для решения вопроса о сходимости не привлекаются другие ряды, и внешние, когда поведение исследуемого ряда сравнивается с поведением некоторого эталонного ряда. Рассмотрим их последовательно.
п. 3 Ряды с положительными членами
Теорема 1 Критерий Больцано
Для
того чтобы ряд
сходился, необходимо и достаточно, чтобы
последовательность
его частичных сумм являлась сходящейся.
Доказательство:
Необходимость.
Пусть
ряд
сходится. Тогда по определению существует
предел
,
т.е. последовательность
является сходящейся. Следовательно,
она ограничена.
Достаточность.
Пусть
последовательность
ограничена. Так как
,
то последовательность
монотонно
возрастает. Тогда существует предел
.
Следовательно, ряд
сходится.
Пример 1
Рассмотрим
ряд:
.
Тогда
.
Заметим,
что
,
,
… .
Таким
образом,
.
Так как правая часть неравенства
является суммой бесконечно убывающей
геометрической прогрессии с
,
,
то
,
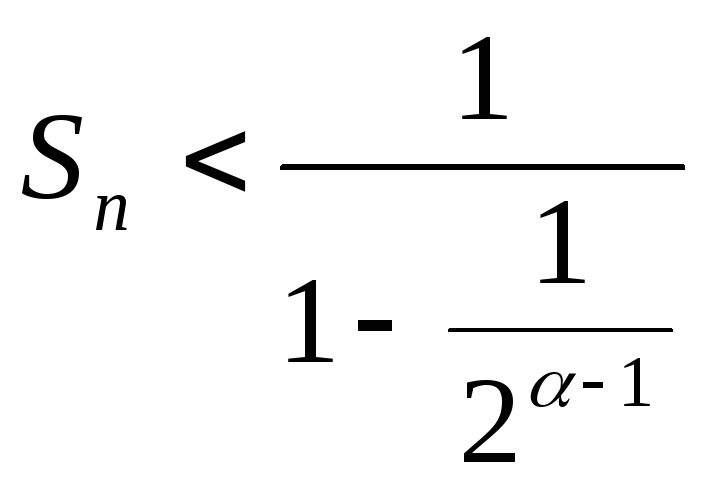т.е. последовательность
ограничена. Тогда по критерию Больцано
ряд
сходится.
Определение 1
Пусть
и
-
ряды с положительными членами. Если
найдется номер
такой, что
,
то ряд
называют мажорантой
ряда
,
а ряд
называют минорантой
ряда
.
Теорема 2 Теорема о мажоранте
Пусть
ряд
является мажорантой
ряда
.
Тогда:
-
если ряд
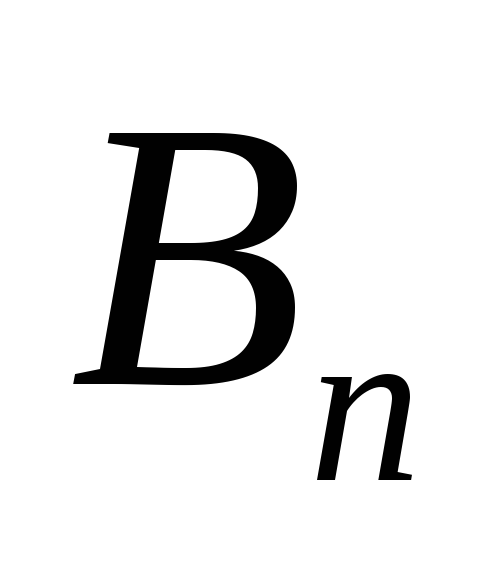сходится, то сходится и ряд
; -
если ряд
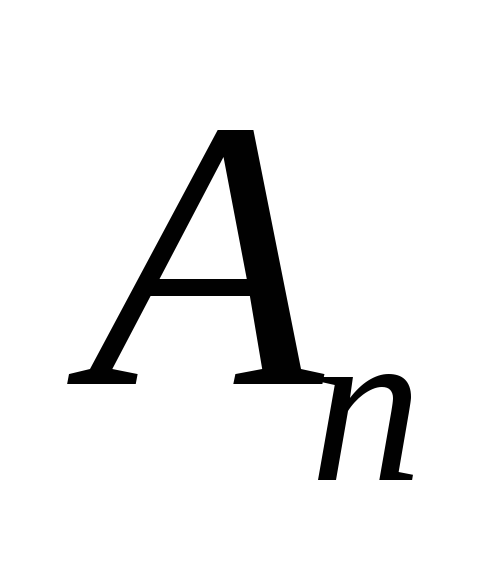расходится, то расходится и ряд
.
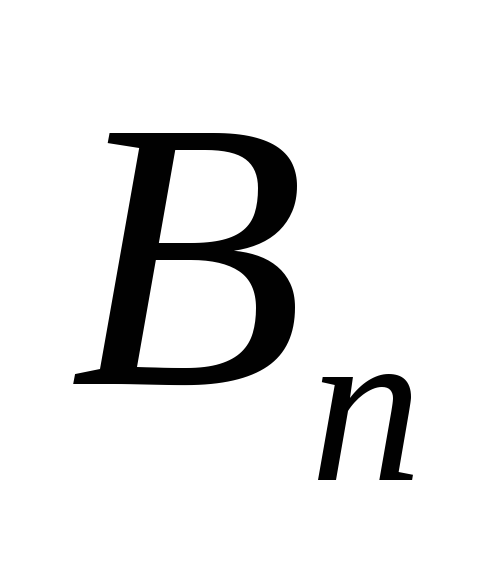Доказательство:
1.
Пусть ряд
сходится. Так как, начиная с некоторого
номера
,
выполняется неравенст-
во:
,
то
.
По условию ряд
сходится. Следовательно, последовательность
его частичных сумм ограничена. Тогда
ограниченной будет последовательность
частичных сумм ряда
,
что означает его сходимость. Значит,
сходится и ряд
.
2.
Пусть ряд
расходится. Предположим противное, т.е.
ряд
сходится. Тогда из пункта 1 данной теоремы
следует, что ряд
сходится. Получили противоречие.
Следствие 2
Пусть
и
-
ряды с положительными членами. Тогда,
если существует конечный предел
,
то ряды сходятся или расходятся
одновременно.
Доказательство:
Пусть
существует конечный предел
.
Тогда найдется такой номер
,
начиная с которого выполняется неравенство
,
или
.
По теореме 5 из правой части неравенства
и сходимости ряда
следует сходимость ряда
.
Если же ряд
расходится, то из левой части неравенства
по теореме 5 следует расходимость ряда
.
Пример 2
Рассмотрим
ряд
.
Так как для любого
выполняется неравенство
,
и ряд
расходится
,
то исходный ряд по теореме 2 расходится.
Пример 3
Рассмотрим
ряд
.
Так как ряд
сходится
,
и
,
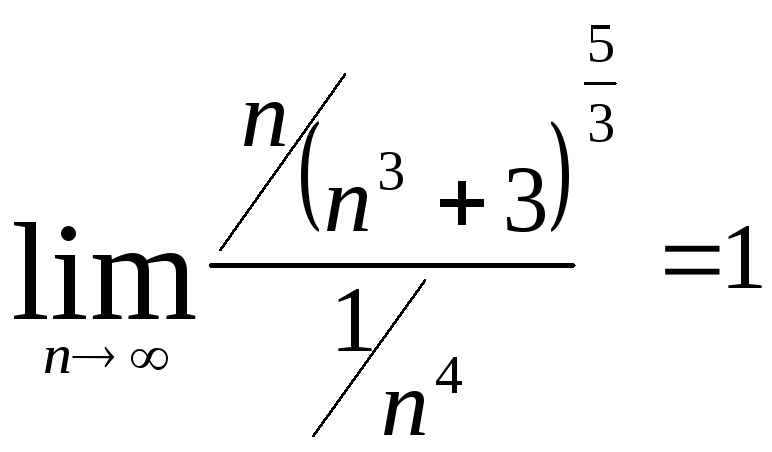то по следствию из теоремы 2 исходный
ряд сходится.
Теорема 3 Признак Даламбера
Пусть
ряд
с положительными членами. Тогда:
а) если
,
то ряд
сходится;
б) если
,
то ряд
сходится при
и расходится при
.
Доказательство:
Пусть
.
Представим
.
Тогда
,
.
Так как ряд
сходится, то сходится ряд
(в силу теоремы 5 о мажоранте). Если
,
то
.
Так как
,
то ряд
расходится, следующий член ряда
не стремится к нулю. Пусть
.
Тогда найдется номер
,
начиная с которого
или
.
Если
,
то
.
Тогда в силу теоремы 5 о мажоранте ряд
сходится. Если же
,
то
.
Тогда в силу той же теоремы ряд
расходится.
Замечание 1
Важно,
что
.
Например, для гармонического ряда
,
но ряд расходится, так как величина
не является константой.
Пример 3
Рассмотрим
ряд
.
Тогда
.
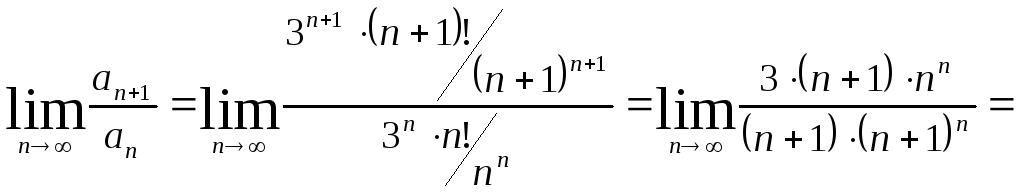
По признаку Даламбера исходный ряд расходится.
Пример 4
Рассмотрим
ряд
.
Тогда
.
По признаку Даламбера исходный ряд
сходится.
Теорема 4 Радикальный Признак Коши
Пусть
ряд
с положительными членами. Тогда:
а) если
,
то ряд
сходится;
б) если
,
то ряд
сходится при
и расходится при
.
Доказательство:
Пусть
.
Тогда
.
Так как
,
то ряд
сходится (это БУГП), то сходится ряд
.
Пусть
.
Тогда найдется номер
,
начиная с которого
или
.
Если
,
то
,
и ряд
сходится. Тогда в силу теоремы о мажоранте
сходится ряд
.
Если
,
то
.
Тогда в силу теоремы о мажоранте
расходится ряд
.
Пример 5
Рассмотрим
ряд:
.
Тогда
.
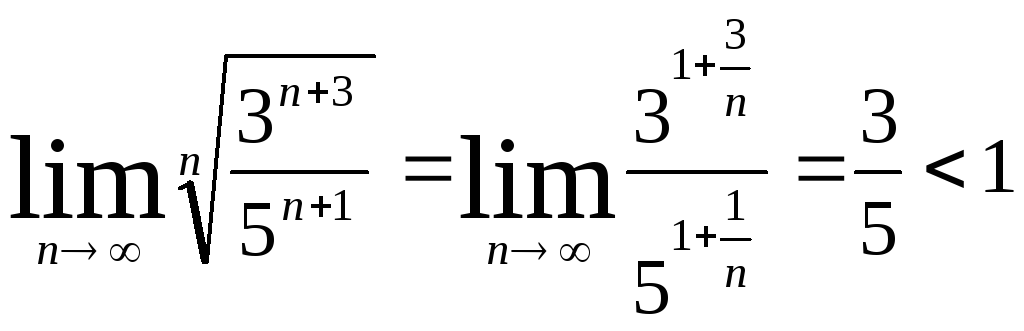По признаку Коши ряд сходится.
Пример 6:
Рассмотрим
ряд:
.
Тогда
.
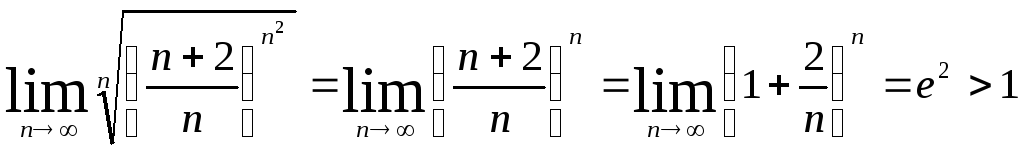По признаку Коши ряд расходится.
Теорема 5 Теорема Дирихле
Если ряд
сходится, то ряд
,
полученный из ряда
перестановкой его членов (заново
перенумерованный), тоже сходится и имеет
ту же сумму.
Доказательство:
Пусть
-
-я
частичная сумма ряда
.
Ее члены находятся в ряде
под некоторыми номерами
.
Пусть
- наибольшее число среди них и
-
-я
частичная сумма ряда
.
Очевидно, что
,
(
-
сумма ряда
)
и так как
произвольно, то ряд
сходится и имеет сумму
.