4.3. Построение базиса в операторном -пространстве для ивс модульного типа

При построении интегрирующих вычислительных структур модульного типа синтезируется математическая модель структуры, исходной предпосылкой для которой является операторный базис для некоторого множества функций [30, 36].

Пусть на ИВС решаются задачи, описывающиеся системой функций из функционального R-пространства [92]. Математической моделью архитектурной единицы модульной ИВС - функционального модуля является Т-оператор, принадлежащий операторному -пространству [29]. Для эффективного представления задач в ИВС необходимо иметь такой набор ФМ, на котором можно было бы настроить любой оператор, входящий в операторное изображение решаемой задачи. Это равносильно тому, что в -пространстве ставится проблема построения базиса операторов, через которые можно было бы представить все Τ-операторы из . Если рассмотреть пространства  и R, то можно установить следующее:

1) при исследовании пар и, где имеем, что T_i-оператор, действующий на функцию S_i , а S_i - соответственно его главное значение, так как по определению [29]

или_.

Иными словами, модно задать некоторое отображение Г между множествами  и R (или  и SR), которое каждому элементу ставит в соответствие элемент и отображение , которое элементу ставит в соответствие элемент _;

2) В общем случае в выражении

только в некоторых частных случаях , например, если. Следовательно, дляГ необходимо уже рассматривать конструкции вида или , где Поэтому отображение Г неоднозначно. Этот факт отмечался, как наличие побочных значений у Τ-оператора.

Исходя из этих предпосылок, для системы функций SR в -пространстве построим локальные базисы и дадим их интерпретацию в терминах задачи нахождения базиса для модульных ИВС.

Рассмотрим процедуру построения локальных базисов. Задана система функций , которая представляет собой задачу, решаемую на ИВС. Необходимо определить дляS базис из Τ-операторов, т.е. определить в операторном  пространстве некоторое множество Т-операторов, при помощи которых можно реализовать систему S.

Представим алгоритм конструирования базиса в следующем виде:

1°. Для полагаем j = 1, т.е. выбираем функцию S₁.

2°. Определяем как _,

где - некоторое подмножество функций , причем, в общем случае, в есть

3°. Строим множество как

4°. Если , то - прообраз базиса в R; следовательно, иначе переходим к п. 5°.

5°. Неравенство говорит о том, что в S есть функции , для которых в нет Τ -операторов.

6°. Для полагаем j = 2, т.е. выбираем функцию S₂.

7°. Определяем F², как ,

где - некоторое подмножество функций , аналогичное.

8°. Строим множество как.

9°. Если , тоF² - прообраз базиса в R ; следовательно, иначе переходим к п, 10°.

10°. Строим множество , гдеF определяется из

.

11. Если , тоF - прообраз базиса в R; следовательно, , иначе переходим к п. 12°.

12°.

N° . . .; следовательно, где .

Необходимо рассмотреть результирующее множество по сравнению с системой.

1. Если , то базис , кроме системыS, может реализовать (порождать) и некоторую систему . Таким образом,S полностью определяется и полностью определяет систему с В этом случае базис системы S будет называться открытым (обозначается), и системаS для - открытая, т.е.

2. Если , то полностью определяет S и будет называться замкнутым базисом системы (обозначается ), и системаS для - замкнутая, т.е.

Произведем оптимизацию базиса. Имеет смысл говорить о с точки зрения минимума числа членов в F , гдеили с точки зрения минимума числа операторов в сумме где каждый член в R - пространстве имеет .

Возможна, например, следующая ситуация. Задана система . При определении получались множества элементов вида . Для всех , т.е. для всех операторовмножества и результирующие определили базис . Очевидно, что - не оптимальный базис.

Рассмотрим суммы операторов и . ВR-пространстве это, соответственно, множества и

Для них и , т. е.

- суть прообразы базисов с минимальным числом членов в или в . Далее можно определить, что

1) 2) _. Следовательно, , т.е. базис, дающий вR множества , более предпочтителен, так как

Таким образом, для минимального базиса в R - пространстве должно выполняться условие или причем Для приведенного примера и

Т е о р е м а 4.1. Если для системы функций S  R локальный базис в операторном -пространстве замкнут, то 1) либо он является минимальным, 2) либо его можно привести к минимальному, т.е. если базис, то всегда существует

До к а з а т е л ь с т в о. Предположим, что имеется множество операторов таких, что В этом случае

_{- прообраз в R операторного базиса , который является минимальным для данной системы S. Пусть для некоторых пар} , тогда для всех этих (i, j) определя-ется сумма и как , причем

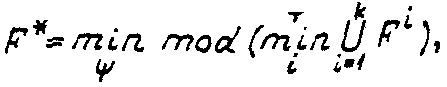где В противном случае базис, для которого определено множествоF был бы открытым. Следовательно, при переборе всех возможных пар (i, j), для которых определится множество F^*, или несколько множеств {F^*} с минимальным числом членов , т.е. достигается и из множеств {F^*} выбирается множество F^* с т.е. определяется множество которое есть прообраз базиса

В случае, если , множествоF представим в виде _, где - множество и , порождаемое , причем . Здесь необходимо при минимизации той частиF, которая включает , конструировать выражение вида, где и и определять множества . При множество -прообраз операторного базиса, который минимизирован по числу членов . Если число выражений больше единицы (k>i), то при минимизации по , т.е. при достижении, получается множество вида

которое есть прообраз минимального замкнутого базиса, порождающего систему S.

Таким образом, от базиса , порождающего систему, сделан переход к базису, для которого часть, порождающаяS , минимальна, а часть порождает т.е. .

Т е о р е м а 4.2. Если система S имеет открытый базис, то S имеет и минимальный замкнутый базис .

Доказательство. Действительно, если имеет , то множествоR можно представить как

где - прообраз замкнутого базиса . Тогда по теореме 4.1 для системы S имеется множество которое есть прообраз базиса в  - пространстве и где порождает

С л е д с т в и е 4.1. Любая система S с базисом может быть дополнена до системы S' с , причем_.

Д о к а з а т е л ь с т в о. В систему S включаются функции S_j, которые порождаются , входят в множество _., образующие , причем_..

С л е д с т в и е 4.2. (частный случай). Если имеют, то- прообраз базиса, который не допускает минимизации, т.е.

П р и м е р. Дана система вR-пространстве или . Необходимо построить операторный базис для системыS.

Строим для S множества F:

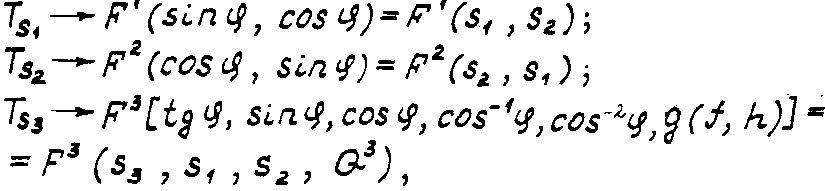
где

.

Определяем базисное множество F . Система открытая, т.к. порождает с элементами .

Вычисляем для .;

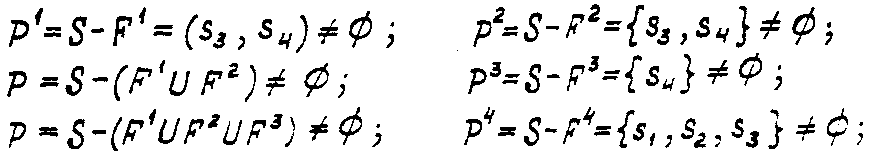
. Следовательно, прообраз базисаΤ-операторов. , поэтому - открытый базис. Для определим . Имеем

Тогда

Здесь

Следовательно, . Открытый базис содержит где - часть оператора , реализующая только (условно). Система условно порождается частью

Тогда часть , которая порождает таким образом

Итак, сконструирован базис для заданной системы S  R, содержащий

При построении локального базиса ( или ) для системыS  R однозначно определяется функционально полный набор модулей ИВС, на которых можно решать все задачи, описываемые S. При этом возможны различные архитектурные решения для функциональных модулей, полученные при использовании заданных критериев оптимальности структуры модуля. Например, можно строить ФМ с максимальным числом элементов для реализации максимально сложного Т-оператора; ФМ для реализации самого простого оператора (что усложняет систему математического обеспечения ИВС, и в частности - систему отображения и настройки); ФМ, оптимальные в смысле средней сложности. С другой стороны, наличие алгоритма построения базиса позволяет синтезировать ИВС переменной мощности, ориентированные на достаточно широкий круг задач.