УМ_Пособие_09

41

Поскольку у5>17.6, то искомой точкой является х5=3.4 т.е. х*=3.4

и f(х*)=17.6.

Преимущество методов Фибоначчи и золотого сечения перед методом дихотомии в том, что при их использовании каждый новый эксперимент приводит к сокращению интервала неопределенности и сохраняется информация о наилучшем результате, тогда как при поиске половинным делением для сокращения интервала требуются два новых измерения. Для иллюстрации эффективности рассмотренных методов приведем таблицу, в которой показано как сокращается интервал неопределенности при n измерениях.

Метод Фибоначчи можно распространить для поиска на конечном дискретном наборе точек.

L0/Ln

Методы поиска, основанные на аппроксимации целевой функции

Суть этих методов заключается в том, что по полученной в ходе вычислений информации строится аппроксимирующая функция и еѐ минимум принимается за точку очередного

42

вычисления. Такие методы дают хорошие результаты при оптимизации достаточно гладких унимодальных функций.

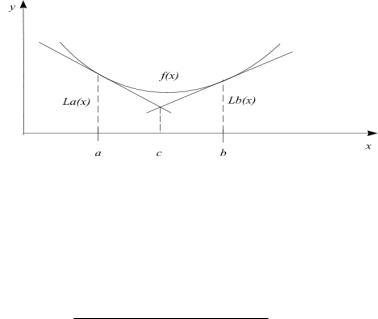
Метод касательных

Пусть функция f (x) выпукла и дифференцируема на отрезке [a,b]. Идея метода состоит в следующем. Пусть [a,b] - отрезок неопределѐнности и f (a), f (a), f (b), f (b) -

результаты вычислений в точках а и b значения функции и ее производной. По этой информации строится аппроксимирующая функция, представляющую из себя

Рис. 9

Полученная аппроксимирующая функция есть ломаная, состоящая из прямой La (x) на отрезке [a,c] и Lb (x) на отрезке [c,b] , где с – точка пересечения касательных. Легко заметить, что при f (a) 0 и f (b) 0 минимум

аппроксимирующей функции достигается в точке с. Значение точки пересечения с можно определить по формуле

c (bf (b) af (a)) ( f (b) f (a))

f(b) f (a)

Вточке с производятся вычисления f (c) и f (c) . Если

f (c) 0 , то решением задачи будет x* c . Если же f (c) 0 ,

43

то в качестве следующего отрезка неопределѐнности будет

данный пункт алгоритма повторяется.

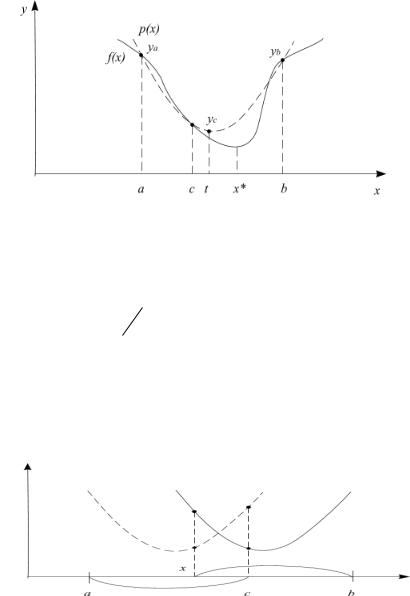
Метод парабол

В этом методе в качестве аппроксимирующей функции используется парабола. Для однозначного задания параболы необходимы три точки. Пусть имеются три точки, для которых выполняются условия: a<c<b, f(c) f(a), f(c) f(b). Так как [a,b]

– отрезок неопределенности и f(x) – унимодальная функция, то найти такую точку c нетрудно. Парабола, проходящая через три точки (a,f(a)), (c,f(c)), (b,f(b)), имеет вид

Поскольку f – унимодальная функция, то хотя бы одно из неравенств f(c) f(a), f(c) f(b) строгое и, следовательно, коэффициент при старшем члене P(x) положителен. Тогда P(x) достигает минимума в точке

t c 1 (b c)2 ( f (a) f (c)) (c a) 2 ( f (b) f (c)) , 2 (b c)( f (a) f (c)) (c a)( f (b) f (c))

44

причем (a+c)/2 t (c+b)/2. Эта точка и выбирается в качестве точки очередного вычисления значения функции (рис.10).

Рис. 10

Если оказалось, что t=c, условимся в качестве точки очередного вычисления выбирать точку (a+c)/2. Итак, следующее вычисление проводится в точке

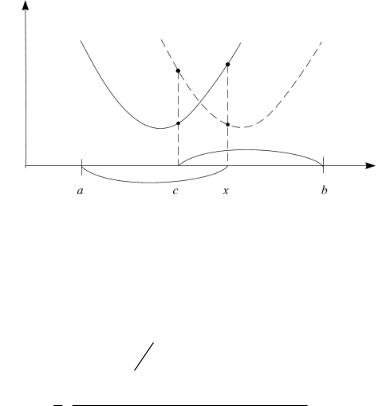
Определим новый отрезок неопределенности с лежащей внутри него точкой, для которой выполняются условия аналогичные условиям, которым удовлетворяла точка c. В силу унимодальности функции f и в зависимости от выполнения или невыполнения условий x<c, f(x)<f(c), f(x)=f(c) это будут отрезки с точкой внутри: [a,c] и x; [x,b] и c; [x,c] и (x+c)/2; [a,x] и c; [c,b]

и x; [c,x] и (x+c)/2 (рис.11 и рис.12).

Рис.11

45

Рис. 12

Далее строится парабола, определяется ее минимум, и т.д., до тех пор, пока длина отрезка неопределенности не будет удовлетворять заданной точности.

Схема алгоритма метода парабол следующая. 1. Задаются a,c,b и . Вычислить ya=f(a), yc=f(c), yb=f(b).

t c 1 (b c)2 ( ya yc ) (c a)2 ( yb yc ) . 2 (b c)(ya yc ) (c a)(yb yc )

3. а) При x<c:

если y<yc, то b=c, c=x, yb=yc, yc=y. если y>yc, то a=x, ya=y.

если y=yc, то a=x, b=c, c=(x+c)/2, ya=y, yb=yc,

yc=f(c).

в) При x>c:

если y<yc, то a=c, c=x, ya=yc, yc=y. если y>yc, то b=x, yb=y.

если y=yc, то a=c, b=x, c=(x+c)/2, ya=yc, yb=y,

противном случае перейти к пункту 2.

46

Упражнения 2

1.Определить положение максимума функции у=4х-х2-3,

заданной на интервале хнач=0, хк=5: а) методом дихотомии, б) методом Фибоначчи при =0.01L0; l0=0.1L0. в) методом

Положение максимума требуется найти с точностью до 0.05.

3.Найти минимум функции f(x)=x2-4x+3 при 0 х 4 одним из методов последовательного поиска.

7.Найти экстремум функции f(x)=- | x | e10x при -1 х 0 с точностью =10-3.

8.Найти экстремум функции f(x)=- 10cos x ex при 0 х 3 с точностью =5*10-4.

9.Покажите, как влияет величина , соответствующая минимальному расстоянию между экспериментами, на сокращение интервала неопределенности при пассивном поиске.

10.Привести формальное решение задачи определения положения точек измерений, чтобы в результате максимально сократился интервал неопределенности в наихудшем случае: а) для двух измерений; б) для трех измерений.

47

ГРАДИЕНТНЫЙ ПОИСК

Как известно, градиент функции в некоторой точке xk направлен в сторону наискорейшего локального возрастания функции и перпендикулярен линии уровня (поверхности постоянного значения) функции f(x), проходящей через точку xk. Вектор, противоположный градиенту f’(xk), называется антиградиентом и направлен в сторону наискорейшего убывания функции f(x). Выбирая в качестве направления спуска pk антиградиент -f’(xk), в точке xk, мы приходим к итерационному процессу вида:

xk+1 = xk - k f’(xk), k>0, k=0,1,2,… .

В координатной форме этот процесс записывается

Все итерационные процессы, в которых направление движения на каждом шаге совпадает с градиентом или антиградиентом функции, называются градиентными методами. Они отличаются друг от друга только способом выбора шага k. Существует много различных способов выбора k.

Градиентные методы в задачах без ограничений

Метод релаксации

Этот метод имеет наиболее простую процедуру поиска. Его алгоритм заключается в отыскании осевого направления, вдоль которого функция цели изменяется наиболее сильно. Для этого в начальной точке поиска определяются производные оптимизируемой функции f(X) по всем переменным. Затем выбирается наибольшая по модулю производная, и соответствующая ей переменная изменяется до достижения частного оптимума. В новой точке определяются производные по всем остальным переменным, и осуществляется поиск следующего частного оптимума и т.д.

48

Характер движения по такому алгоритму можно описать следующим образом:

xjk+1 = xjk, j {1,…,n}, j i; xik+1=xik+h sign f ( X p )

xl

где Xр - точка, в которой последний раз определялись производные;

хi, - координата с наибольшей по модулю производной в точке Хр ;

Скорость движения к оптимуму зависит от выбора величины шага изменения независимых переменных. При малом шаге процесс сходится медленно, при завышенной величине шага возможно "рыскание", т.е. многократное проскакивание оптимума.

Теоретически поиск заканчивается, когда все частные производные целевой функции равны 0. Поскольку при измерениях и вычислениях всегда существует погрешность, то в качестве критерия окончания поиска принимают условие

где - некоторое заранее заданное малое число. Пример. Найти минимум функции f(X)=x12+ x22+1.2 x1x2 методом релаксации.

Так как функция зависит лишь от двух переменных, то метод релаксации совпадает с методом поочередного изменения переменных.

Пусть Х0=(1,2). Освободим х1, оставив х2 закрепленной и

равной х20=2. Тогда имеем

f(x1,x20) = x12 + (x20)2 + l.2x1x20 = х12 + 2.4х1 + 4.

Минимум f(X) находится из условия

f ( X ) = 2x1 + 1.2x20 = 2x1 +2.4 = 0, т.е. координаты новой точки

x1

таковы: x1=x11=-1.2 и х2= х20 =2.

49

Теперь закрепляем координату x1 на новом уровне и изменяем х2. Функция цели опять становится функцией только

одной переменной

f(x11,x2)= (x11)2 + x2(2) + l.2x1(1) = 1.44 + х2(2) - 1.44х2.

Находим ее минимум из условия

f (x1(1) , x2) = 2x2 + 1.2x11 = 2х2-1.44 = 0

x2

и переходим в новую точку x1 = x11 =-1.2; х2 = х2(1) = 0.72.

Градиентный метод с постоянным шагом (равномерный градиентный метод)

Основная проблема в градиентных методах – это выбор шага k. Достаточно малый шаг k обеспечивает убывание функции, то есть выполнение неравенства:

f(xk - kf’( xk))) < f(xk),

но может привести к неприемлемо большому количеству итераций, необходимых для достижения точки минимума. С другой стороны, слишком большой шаг может вызвать неожиданный рост функции (невыполнение условия убывания) либо привести к колебаниям около точки минимума. Однако проверка условия убывания на каждой итерации является довольно трудоемкой, поэтому в методе градиентного спуска с постоянным шагом задают = k постоянным и достаточно малым, чтобы можно было использовать этот шаг на любой итерации. При этом приходится мириться с возможно большим количеством итераций. Утешением является лишь то, что

Пропорциональный градиентный метод

Здесь длина очередного рабочего шага прямо пропорциональна величине градиента изображающей точки, т.е.

Пропорциональный градиентный поиск следует начинать с определения приемлемого значения α. Можно поступить следующим образом. Применив в качестве начальной величины произвольное значение α0 ≤1, на каждом шаге станем уменьшать α вдвое, пока не получим f(хk+1)>f(хk) (при поиске max). Процедуру поиска запишем в виде

xi k 1 xi k k f ( X k ) , i=1,2,…,n;

xi