115
|
|
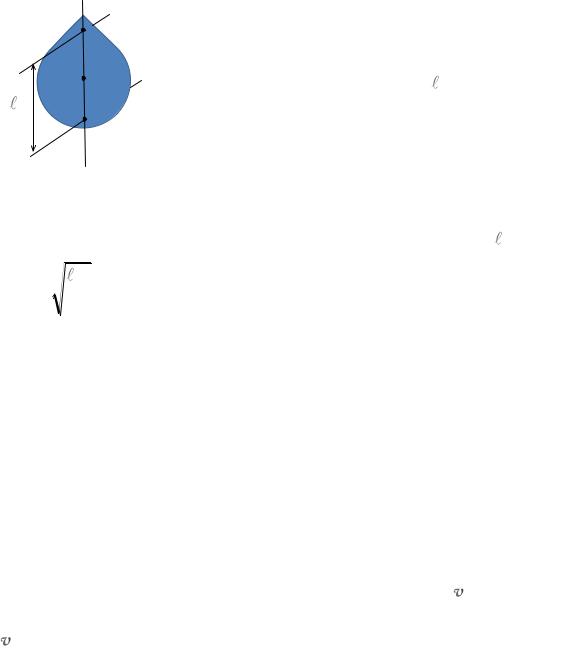
Точку O (рис. 2.12) называют центром качания |
|
О |
физического маятника. Он находится на прямой линии, |
|
|
проходящей через точку подвеса O и центр масс C , и от- |
|
С |
стоит от точки O на расстоянии пр . Если маятник пере- |
|
|
|
пр |
О |
вернуть и заставить совершать малые колебания вокруг |
|
|
|
|
|
оси O , то период колебаний не изменится. Установив |
|
|
экспериментально положения двух «сопряженных» точек, |
|
Рис. 2.12. |
периоды небольших колебаний вокруг которых одинако- |
|
вы, можно измерить ускорение свободного падения. Дей- |
|
|
|
|
ствительно, зная период этих колебаний и расстояние OO пр , из формулы |
||
T 2 |
пр |
находим g . |
|
g |
|||
|
|
2.1.7.Энергия гармонического осциллятора
Осциллятором называют любую физическую систему, совершающую колебания. Классический осциллятор – механическая система, совершающая колебания около положения устойчивого равновесия.
Рассмотрим вопрос об энергии гармонического осциллятора на примере
материальной точки массы |
m , колеблющейся под действием квазиупругой |
||||||||||
силы Fx kx по закону |
|
|
|
|
|
|
|
|
|
||
|
|
|
x Acos( t ) . |
|
|
|
|
|
|||
Кинетическая |
энергия этой точки W |
m 2 |
|
, где |
скорость |
||||||
|
|
||||||||||
|
|
|
|
|
|
k |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A sin( t ) . |
После подстановки скорости в формулу кинетической |
||||||||||
энергии имеем |
|
|
|
|
|
|
|
|
|
|
|
|
W |
m 2 A2 sin2 ( t ) |
|
|
m 2 A2 sin2 |
, |
|
(2.16) |
|||
|
|
|
|
||||||||
|
k |
2 |
|
2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|||
где t — фаза колебаний. |
|
|
|
|
|
|
|
||||
Как известно из |
тригонометрии, |
|
частота колебаний |
функции |
|||||||
sin2 ( t ) больше частоты колебаний функции sin( t ) в два раза, следовательно, кинетическая энергия совершает колебания с циклической частотой равной 2 .
В связи с тем, что гармонические колебания совершаются под действием квазиупругой силы Fx kx , потенциальную энергию колеблющейся точ-
116
ки найдем по формуле потенциальной энергии упругих сил W |
kx2 |
. Учиты- |
||||||
|
||||||||
|
|
|
|
|
п |
2 |
|
|
|
|
|
|
|
|
|
||
вая, что x Acos( t ) , а коэффициент квазиупругой силы |
|
k m 2 , полу- |
||||||
чим |
|
|
|
|
|
|
|
|
W |
m 2 A2 cos2 ( t ) |
|
m 2 A2 cos2 |
, |
|
|
|
(2.17) |
|
|
|
|
|
||||
п |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Потенциальная энергия материальной точки совершает колебания с частотой равной частоте колебаний функции cos2 ( t ) , т. е. с циклической частотой 2 .
Из соотношений (2.16) и (2.17) видно, что Wп и Wk изменяются со
сдвигом по фазе на радиан друг относительно друга: когда потенциальная
2
энергия Wп максимальна, кинетическая энергия Wk равна нулю и наоборот. При этом полная энергия осциллятора W сохраняется. Действительно,
W Wk |
Wп |
|
m 2 A2 sin2 |
|
m 2 A2 cos2 |
|
m 2 A2 |
sin2 cos2 , |
||
|
|
|
|
|||||||
|
|
2 |
2 |
|
2 |
|
||||
а, учитывая, что sin2 cos2 1, получим |
|
|
|
|
||||||
|
|
|
|
W |
m 2 A2 |
, |
|
|
(2.18) |
|
|
|
|
|
|
|
|
||||
|
|
|
|
2 |
|
|
|
|
||
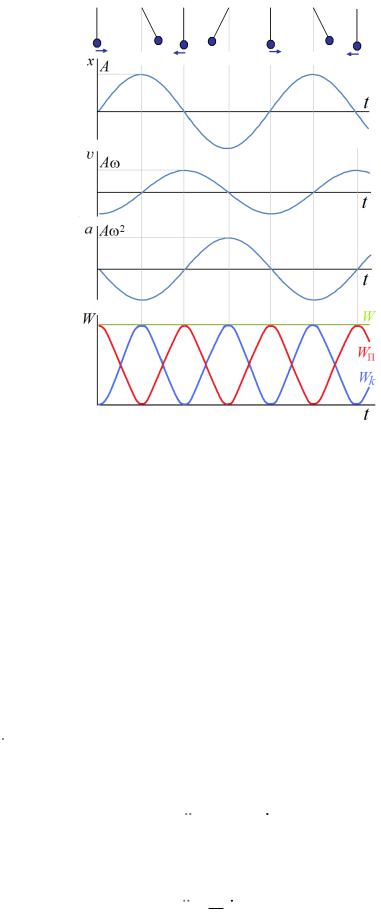
то есть полная энергия колебаний не зависит от времени и остается величиной постоянной. Из формулы (2.19) видно, что неизменная полная энергия W совпадает с потенциальной энергией Wп в точке наибольшего отклонения от положения равновесия при x A и совпадает с кинетической энергией Wк при прохождении материальной точки через положение равновесия, где ее скорость равна A , а х = 0. Изменение со временем координаты колеблющейся точки х, ее скорости v , ускорения а, кинетической Wк , потенциальной Wп и полной энергии W показано на рис. 2.13.
Отметим в заключение, что энергия осциллятора прямо пропорциональна квадрату амплитуды колебаний W A2 .
117
Рис. 2.13.
2.1.8.Затухающие колебания
2.1.8.1.Уравнение затухающих колебаний
Влюбой реальной колебательной системе действуют силы сопротивления, действие которых приводит к уменьшению амплитуды и энергии колебаний. Такие колебания называют затухающими. Рассмотрим, например,
пружинный маятник, колеблющийся в какой-либо среде. На маятник массы m кроме квазиупругой силы F kx действует сила сопротивления, прямо пропорциональная скорости движения маятника. Проекция этой силы на ось x равна rx , где r коэффициент сопротивления. Тогда уравнение движения (второй закон Ньютона) будет иметь вид:
mx kx rx .
Разделим каждое слагаемое на массу маятника m и перенесем их все в левую часть уравнения, получим x mr x kx 0 . Введѐм следующие обозна-
118
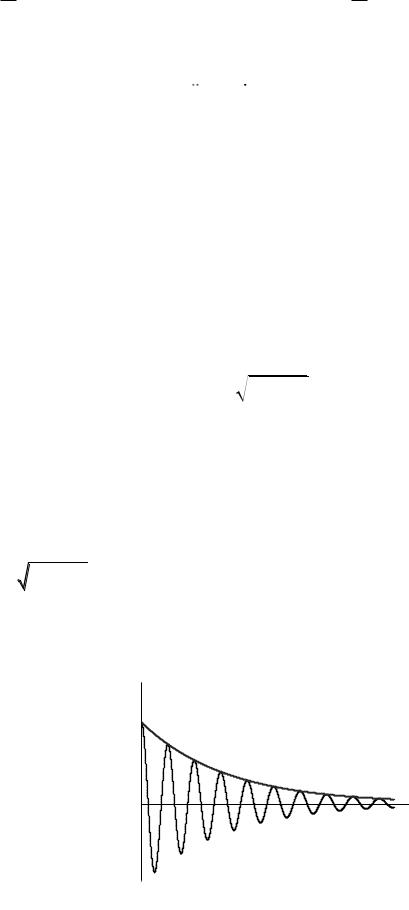
чения: mr 2 , где коэффициент затухания, mk 02 , где 0 собствен-
ная циклическая частота осциллятора. Тогда уравнение движения примет вид:
x 2 x 02 x 0 .
Мы получили дифференциальное уравнение свободных затухающих ко-
лебаний. Это однородное дифференциальное уравнение второго порядка. Решая его при условии 0 , можно получить интегральное уравнение затухающих колебаний:
x A0e t cos( t ) ,
где A0 и постоянные интегрирования, определяемые из начальных условий, частота затухающих колебаний:
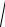02 2 .
Частота затухающих колебаний ω меньше, чем частота колебаний в той же самой системе без затухания ω0.
График x(t) затухающих колебаний показан на рис. 2.14. Из него видно, что эта функция непериодическая. Тем не менее, величину
T |
2 |
|
|
2 |
|
принято называть периодом затухающих колебаний. |
|
|
|
|
|
||||
02 2 |
|||||||
|
|
|
|
||||
Множитель A A0e t называют амплитудой затухающих колебаний. График изменения амплитуды затухающих колебаний со временем показан на рисун-
|
х |
A0 |
|
|
A(t) |
0 |
t |
|
Рис. 2.14.
119
ке 2.14 пунктирной линией.
В момент времени t 0 колеблющаяся величина x будет равна x A0 cos , в силу этого величину A0 называют начальной амплитудой колебаний, а величину называют начальной фазой затухающих колебаний.
2.1.8.2.Характеристики затухания
Кроме коэффициента затухания затухающие колебания характеризуют и другими величинами, такими как:
1.Время релаксации это время, за которое амплитуда колебаний
|
|
|
|
e |
A e t |
|
|
A e t |
|
|
||||
уменьшается в e раз. |
По определению |
0 |
|
0 |
|
|
|
. После со- |
||||||
A e (t ) |
|
A e te |
||||||||||||
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
кращений получим e |
1 |
e , т. е. |
1, или |
|
1 |
|
; |
|
1 |
. Как видим, |
||||
e |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
коэффициент затухания есть величина обратная времени релаксации. Коэф-
|
1 |
|
фициент затухания измеряется в секундах в минус первой степени |
|
. |
|
||
c |
|
|
2. Логарифмический декремент затухания это натуральный лога-
рифм отношения значений амплитуд, соответствующих моментам времени, отличающихся на один период. По определению
ln |
|
A e t |
ln |
A e t |
. После сокращений получим ln e t , т. е. |
|
|
|||||
|
0 |
0 |
|
|
|
|||||||
|
A e (t T ) |
A e t e T |
|
|
||||||||
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T . |
|
|
|
|
|
|
|
Число колебаний N |
, совершенных за время релаксации, равно N |
, |
|||||||||
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тогда логарифмический декремент затухания |
1 |
T |
1 |
. То есть логариф- |
||||||||
|
|
|||||||||||
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
мический декремент затухания обратен числу колебаний, совершенных осциллятором за время релаксации.
3. Добротность колебательной системы. Вынесем этот вопрос отдельным параграфом.