3. Обратное интерполирование (вычисление X при заданной y).

Полином Лагранжа-многочлен минимальной степени, принимающий данные значения в данном наборе точек. Для  n+1 пар чисел (x₀, y₀), (x₁, y₁),..., (x_n, y_n), где все x_j различны, существует единственный многочлен степени не более, для которого. В простейшем случае (n=1)— это линейный многочлен, график которого — прямая, проходящая через две заданные точки.

4. Интерполяция функции нескольких переменных.

Билинейная интерполяция — в вычислительной математике расширение линейной интерполяции для функций двух переменных. Ключевая идея заключается в том, чтобы провести обычную линейную интерполяцию сначала в одном направлении, затем в другом.

Недостаток метода:

Главным минусом билинейной интерполяции при масштабировании изображений является тот факт, что при увеличении в раз изображения размером на пикселей в результате будет получено изображение размером не на пикселей, а на пикселей.

Связано это с тем, что в исходном изображении, например, по горизонтали имеется точек, то есть смежных пар. При увеличении изображения в раз между каждой парой основных точек вставляется дополнительных точек (то есть при увеличении вдвое между основными точками вставляется еще по одной, при увеличении втрое — по две и т. д.). Итого в результате ширина результирующего изображения будет равна сумме количества основных и дополнительных точек:проще говоря, для последнего пикселя (в каждой строке и столбце) исходного изображения не находится пары, с которой можно было бы провести интерполирование.

Бикубическая интерполяция -в вычислительной математике расширение кубической интерполяции на случай функции двух переменных, значения которой заданы на двумерной регулярной сетке. Поверхность, полученная в результате бикубической интерполяции является гладкой функцией, в отличие от поверхностей, полученных в результате билинейной интерполяции или интерполяции методом ближайшего соседа. Так же бикубическая интерполяция часто используется в обработке изображений, давая более качественное изображение по сравнению с билинейной интерполяцией.

5. Другие способы интерполяции.

Рациональная интерполяция - представление интерполируемой функции (точнее говоря, ряда табличных значений) в виде отношения двух полиномов. Ряд функций, плохо интерполируемых полиномиальными методами, удаётся хорошо приблизить рациональной функцией с полиномом в числителе и знаменателе. Особенно это касается функций с нерегулярным характером поведения (в частности, рациональная интерполяция хорошо подходит для функций с особыми точками резкими изменениями) [1].

2. Подробное описание двух методов на выбор

3.1 Кубический сплайн.

Кубические сплайны - это мощное и удобное средство, но и они небезупречны: необходимо учитывать влияние направления и величины касательных векторов, указывать все точки кривой до ее изображения, невозможна локальная коррекция кривой. Последнее особенно важно для интерактивной работы. Расчет кубического сплайна требует обращения большой матрицы, зависящей от всех элементов сплайна; т.е. изменение любого сегмента затрагивает все остальные сегменты. Воздействие уменьшается при удалении от точки возмущения, но полностью пренебречь им нельзя. Параболическая интерполяция разрешает большинство этих проблем за счет того, что она только непрерывна, т. е. в точках соединения сегментов сохраняется непрерывность лишь первой производной. Для многих прикладных задач этого достаточно, причем параболическая интерполяция не требует больших расчетов.

Параболическая интерполяция была разработана Оверхаузером [3-1]. Оверхаузер строил кривую интерполяции, исходя из геометрических соображений. Идея состоит в линейной интерполяции пересекающихся частей двух парабол. Параболы заданы четырьмя последовательными точками: первая - тремя первыми точками, вторая - тремя последними. Пересечение лежит между второй и третьей точками.

Рисунок 3-1. Параболическая интерполяция.

Несмотря на то, что параболы-плоские кривые, их линейная интерполяция это кубическая пространственная кривая, как показано

на рис. 3-1.

Рассмотрим обобщенный вывод для всего семейства. Параболически интерполированная кривая имеет вид

С (t) = (1-t) p (r) + t q (s),                (3-1)

Гдеr, s, t - параметры, p(r), q(s)  - параметрические параболы, проходящие через P₁, P₂, P3 и P₂, P₃, P₄, соответственно, как показано на рис. 3-2. Для простоты параболы на рис. 3-2 лежат в одной плоскости, но это не обязательно (рис. 1-18). Параметрическое представление p(r) и q(s) следующее:

p (r) = [r²  r    1] [B],                 (3-2)

q (s) = [s² s 1] [D],                     (3-3)

где [B] и [D] - матрицы, представляющие положение вектор-точек  P₁, P₂, P₃ и P₂, P₃, P₄, соответственно. Результат интерполяции - кубическая кривая

C (t) = [t3 t2 t 1] [A] [G] = [T] [A] [G],                      (3-4)

Рисунок 3-2 Обозначение для параболической интерполяции.

Чтобы определить [B] и [D], а затем [A] и [G], необходимо установить связь между параметрами r, s, t. Из рис. 3-2, замечая, что r меняется от 0 до 1 на сегменте от P₁ до P₃ вдоль p(r), s меняется от 0 до 1 на сегменте от P₂ до P₄ вдоль q(s), и t меняется от 0 до 1 на сегменте от P₂ до P₄ вдоль C(t), разумно предположить, что  r и t, а также s и t связаны линейно. Отсюда

r = k₁t+k₂,                s = k₃t+k₄,                 (3-5)

где k_i - константы, заданные граничными условиями в вектор-точках P₁, P₂, P₃ и P₄. Предположим, что данные распределены равномерно или почти равномерно, и диапазон параметров нормализован, т.е. 0. Тогда можно условиться, что

p (0) = P₁,                  p (1\2) = P₂,   p (1) = P₃,                  (3-6а)

q (0) = P₂,                  q (1\2) = P₃,    q (1) = P₄,                   (3-6b)

C (0) = P₂,                                      C (1) = P₄.                  (3-6с)

Здесь основные предположения таковы: p(r)=P₂ для r=1\2 и q(s)=P₃ для s=1\2. В результате получаем единственный член семейства параболических интерполированных кривых, как будет показано ниже.

В предположениях уравнений (3-5)

P₂: r=1\2, t=0₂=1\2

P₃: r=1, t=1k₁+k₂=1k₁=1\2

P₂: s=0, t=0k₄=0

P₃: s=1\2, t=1k₃=1\2

И так

r (t) =(1+t),       s(t)=t   .                  (3-7)

Вспомним уравнение (3-2) и используем уравнение (3-6а), чтобы выразить [B] через P₁, P₂, P₃,

p (0) = P₁ = [B],(3-8а)

p (1\2) = P₂ = [1\4 1\2 1] [B],       (3-8b)

p (1) = P₃ = [1 1 1] [B].      (3-8с)

Запишем в виде одной матрицы

.

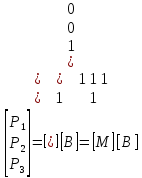Отсюда

[B]= =  .                (3-9)

Аналогично через P₂, P₃, P₄ находится выражение [D]. Пользуясь уравнением (3-6b), получаем

q (0) = P₂ = [0 0 1] [D],     (3-10a)

q (1\2) = P₃ = [ 1\4 1\2 1] [D],        (3-10b)

q (1) = P₄= [1 1 1] [D].       (3-10c)

Сравнение с уравнениями (3-8) сразу же дает

=   .(3-11)

Вспомним уравнение (3-1) и подставим уравнения (3-2) и (3-3):

C (t) = (1-t) [r² r 1] [B] + t [s² s 1] [D].

Используем уравнение (3-7), чтобы переписать это только в терминах параметра t,

C (t) = +.

Подставив [B] и [D] из уравнений (3-9) и (3-11), получим

C (t) = +

Перепишем уравнение так, чтобы включить все четыре точки P₁, P₂, P₃, P₄:

C(t)==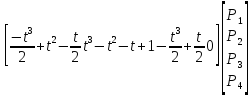

Наконец, перепишем результат в форме уравнения (3-4)

C (t) = [t³ t² t 1] [A][G]=[T][A][G],                        (3-4)

где

[A]=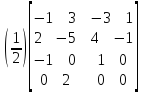(3-12)

и

[G]^T=[P₁ P₂ P₃ P₄].                (3-13)

Заметим, что результат имеет вид произведения матрицы интерполяционных функций и геометрической матрицы [2].