Davis W.A.Radio frequency circuit design.2001

180 RF POWER AMPLIFIERS

Evaluation of the integral makes use of the trigonometric identity, cos ˛ š ˇ D cos ˛ cos ˇ Ý sin ˛ sin ˇ. From Eq. (9.36) the dc current is

This gives the dc current from the power supply in terms of IOC and the conduction angle , so power supplied by the source is

The ac component of the current flows through the blocking capacitor and into the load. Harmonic current components are shorted to ground by the tuned circuit. The magnitude of the output voltage at the fundamental frequency is found using the Fourier method:

The quiescent current term, IC, is replaced by Eq. (9.37) again, and the trigonometric identity for sin ˛ cos ˇ is used:

The efficiency (neglecting the input power) is simply the ratio of the output ac power to the input dc power. The maximum output power occurs when VO O D

power. Nevertheless, Figs. 9.11 and 9.12 indicate the trade-offs in choosing the appropriate conduction angle for class C operation.

9.4CLASS C INPUT BIAS VOLTAGE

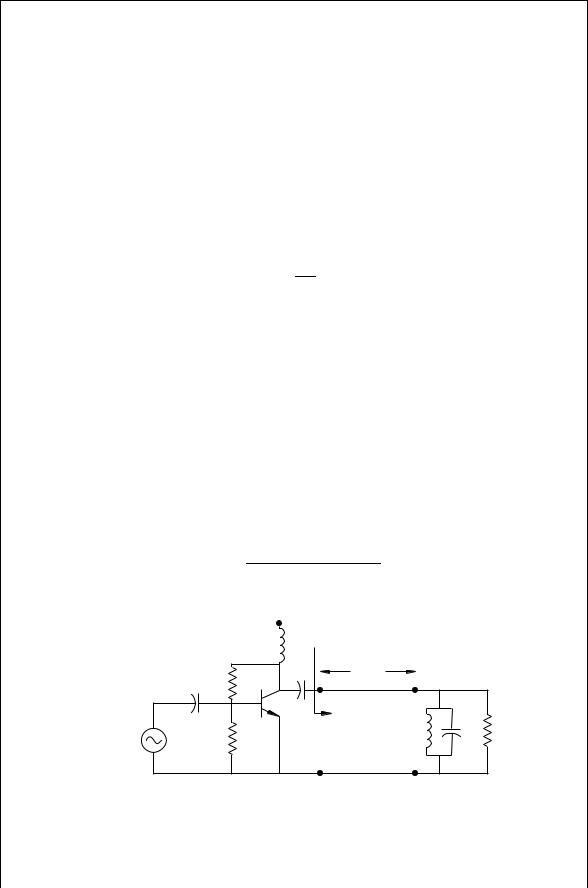
Device SPICE models for RF power transistors are relatively rare. Manufacturers often do supply optimum generator and load impedances that have been found to provide the rated output power for the designated frequency. The circuit shown in Fig. 9.9 is a generic example of a 900 MHz amplifier with a bandwidth of 18 MHz in which the manufacturer has determined empirically the optimum ZG and ZL. The Q of the output tuned circuit then is

The Q determines the inductance and capacitance of the output resonant circuit:

Furthermore, if the desired output power is POmax, the collector voltage source, VCC, and the maximum collector current is icmax, then the average to peak power ratio, r, is found from Eqs. (9.49) and (9.54). Iterative solution of Eq. (9.54) gives the value for the conduction angle, . This will then allow for estimation of the maximum efficiency from Eq. (9.48). Alternatively, for a given desired efficiency, the conduction angle, , can be obtained by iterative solution of Eq. (9.48). Numerically it is useful to take the natural logarithm of Eq. (9.48) before searching iteratively for a solution:

The efficiency expression can be modified to account for the non zero saturation collector–emitter voltage.

To achieve the desired conduction angle, the emitter–base junction must be biased so that the transistor will be in conduction for the desired portion of the input signal. Collector current flows when VBE > 0.7. First it is necessary to determine the required generator voltage amplitude, VO G, that will produce the desired maximum output current. This is illustrated in Fig. 9.13 where the input ac signal

186 RF POWER AMPLIFIERS

The Fourier expansion of a square wave with amplitude from C1 to 1 and period 2 is

3 5

Consequently, to produce a square wave voltage waveform at the transistor terminal, the load must be a short at even harmonics and large at odd harmonics. Ordinarily only the fundamental second harmonic and third harmonic impedances are determined. In the typical class F amplifier shown in Fig. 9.15, the L1C1 tank circuit is resonant at the output frequency, f0, and the L3C3 tank circuit is resonant at 3f0. It has been pointed out [5] that the blocking capacitor, CB, could be used to provide a short to ground at 2f0 rather than simply acting as a dc block.

The design of the class F amplifier final stage proceeds by first determining C1 from the desired amplifier bandwidth. The circuit Q is assumed to be determined solely by the L1, C1, and RL. Thus

Once C1 is determined, the inductance must be that which resonates the tank at f0:

At 2f0 the L1C1 tank circuit has negative reactance, and the L3C3 tank circuit has positive reactance. The capacitances CB and C3 can be set to provide a short to ground:

On multiplying through Eq. (9.63) by ω0 and recognizing that L3C3 D 1/9ω02, L1C1 D 1/ω02, this equation reduces to

which is the requirement for series resonance at 2f0. In addition, at the fundamental frequency, CB and the L3C3 tank circuit can be tuned to provide no

reactance between the transistor and the load, RL. This eliminates the approximation that the L3C3 has zero reactance at the fundamental:

This value for CB can be substituted back into Eq. (9.64) to give a relationship between C3 and C1:

In summary, C1 is determined by the bandwidth Eq. (9.61), L1 by Eq. (9.62), C3 from Eq. (9.67), L3 from its requirement to resonate C3 at 3f0, and finally CB from Eq. (9.66). These equations are slightly different than those given by [5], but numerically they give very similar results. In addition interstage networks are presented in [5] that aim at reducing the spread in circuit element values, and hence this helps make circuit design practical.

Additional odd harmonics can be controlled by adding resonators that make the collector voltage have a more square shape. In effect an infinite number of odd harmonic resonators can be added if a */4 transmission line at the fundamental frequency replaces the lumped element third harmonic resonator (Fig. 9.16). This of course is useful only in the microwave frequency range where the transmission line length is not overly long.

At the fundamental the admittance seen by the collector is

FIGURE 9.16 Class F transmission line power amplifier. Here CB D 1 µF, Z0 D 20 -, C1 D 936.6 pF, L1 D 33.39 pH, RL D 42.37 -, VCC D 24, R1 D 5 k-, R2 D 145 k-.

188 RF POWER AMPLIFIERS

The */4 transmission line in effect converts the shunt load to a series load:

At the second harmonic, the transmission line is */2 and the resonator L, C

...

While this provides open and short circuits to the collector, it is not obvious that these impedances, which act in parallel with the output impedance of the transistor, will provide the necessary amplitude and phase that would produce a square wave at the collector.

An example of a class F amplifier design using the idealistic default SPICE bipolar transistor model illustrates what these waveforms might look like. As in the class C amplifier example, assume that the center frequency is 900 MHz, that the bandwidth is 18 MHz, and consequently that the circuit Q D 50. Furthermore, as in the class C amplifier example, assume that the collector looks into a load resistance of RL0 D 9.441 - and that Z0 D 20 - is chosen. For the series resonant effective load, the load at the end of the transmission line can be found:

Z2

RL0 D R0 D 42.37 -

L

Q D 50 D ω0L0

RL0

or

L0 D 374.6 nH