43. Основные геометрические параметры зубчатого колеса.

_{Основными параметрами зубчатого колеса являются (рис. 1):}

• z – число зубьев;

• r_a – радиус (диаметр) окружности выступов;

• r_f – радиус (диаметр) окружности впадин;

• r_b – радиус (диаметр) основной окружности;

• r – радиус (диаметр) делительной окружности, т. е. окружности, которая  является  начальной  в станочном зацеплении колеса с режущим инструментом;

• р – шаг по делительной окружности;

• h – высота зуба, равная h=h_a+h_f, где:

1. h_a – высота головки зуба;

2. h_f – высота ножки зуба;

• m – модуль зацепления, определяемый из условия:

, т. е. , (измеряется в мм).

Величина m стандартизирована, а делительная окружность является окружностью стандартного модуля. Обычно размеры зубчатого колеса и зубьев выражаются через m.

Так, например: , где   – коэффициент  высоты головки зуба;

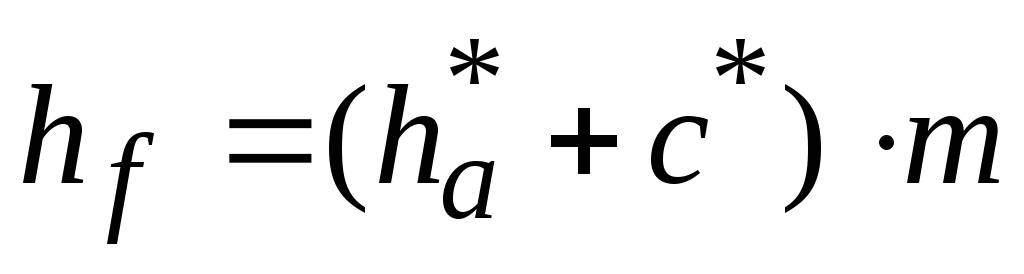, где  - коэффициент  радиального зазора;

;  ;  , где α – угол исходного контура режущего инструмента.

Обычно для стандартных зубчатых колёс: ;  ;    α=20º.

_44а

_44б

44. Свойства эвольвентного зацепления.

_{В зубчатой передаче контактирующие элементы двух профилей выполняются по эвольвентам окружности и образуют, так называемое эвольвентное зацепление. Это зацепление обладает рядом полезных свойств, которые и определяют широкое распространение эвольвентных зубчатых передач в современном машиностроении.}

_{Свойства эвольвентного зацепления:}

• передаточное отношение эвольвентного зацепления определяется только отношением радиусов основных окружностей и является величиной постоянной;

u₁₂=ω₁/ ω₂= r_W2/ r_W1= (r_b2·cos α_W)/ (r_b1·cos α_W)= r_b2/ r_b1=const.

• при изменении межосевого расстояния в эвольвентном зацеплении его передаточное отношение не изменяется;

• при изменении межосевого расстояния в эвольвентном зацеплении величина произведения межосевого расстояния на косинус угла зацепления не изменяется.

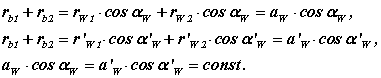
• за пределами отрезка линии зацепления N₁N₂ рассматриваемые ветви эвольвент не имеют общей нормали, т. е. профили выполненные по этим кривым будут не касаться, а пересекаться. Это явление называется интерференцией эвольвент или заклиниванием.

45. Качественные показатели зубчатого зацепления.

Одним из качественных показателей зубчатой передачи является коэффициент перекрытия ε_α, равный ε_α=g_α/p_α, где p_α – шаг по основной окружности (расстояние между одноименными точками двух соседних зубьев, замеренное по дуге основной окружности). Коэффициент ε_α показывает сколько пар зубьев в среднем одновременно находиться в зацеплении. Для прямозубой передачи обычно 1< ε_α<2. Чем больше ε_α, тем более плавно и бесшумно работает передача.

Другим качественным показателем является коэффициент скольжения, который учитывает влияние геометрии передачи и ее кинематики на скольжение и износ профилей, скользящих друг по другу (рис. 74), что видно из картины скоростей. На этой картине:

V_k1 – скорость точки К первого колеса;

V_k1^t – проекция этой скорости на касательную к контактирующим профилям;

V_k2 и V_k2^t – тоже для колеса 2.

Скорость скольжения колеса 1 и 2 относительно друг друга равна:

V_ck=V_k1k2= V_k1^t- V_k2^t

Коэффициенты скольжения колес 1 и 2 равны:

;

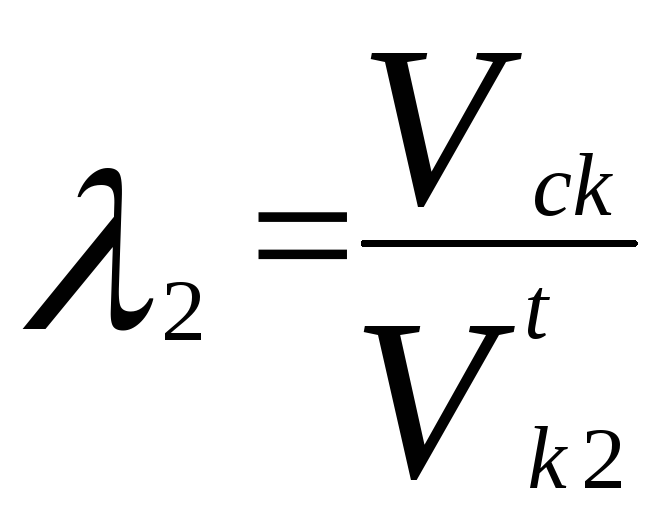
Эти коэффициенты равны нулю в полюсе (точка Р) и увеличиваются с удалением от него по линии зацепления.

46а

_46б