1.2 Составление элементарных матриц параметров режима сети и матриц соединений

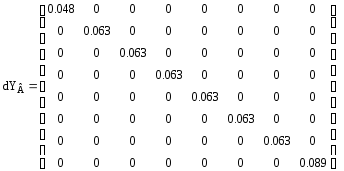
Составим квадратную диагональную матрицу [dZв ] по уже известным сопротивлениям, а также квадратную матрицу узловых проводимостей []:

_См

Первая матрица инциденций:

Где [ ] - матрица соединений для ветвей дерева;

[ ] - матрица соединений для хорд.

Вторая матрица инциденций:

1.3 Расчет матрицы узловых проводимостей и матрицы контурных сопротивлений

Найдем матрицу узловых проводимостей [] (без учета балансирующего узла) по формуле:

Матрица узловых проводимостей [] (с учетом балансирующего узла) определяется по формуле:

Матрица является вырожденной матрицей, т.е. нахождение для неё обратной не представляется возможным. Это подтверждается тем, что при суммировании элементов строк Y получается нулевая строка, и, следовательно, определитель этой матрицы, вычисленный по теореме разложения определителя по элементам строки (столбца ), обращается в 0, т .е . det

Матрица контурных сопротивлений находится из выражения:

Получили симметричную матрицу 3-го порядка.

1.4 Составление узловых уравнений установившегося режима электрической сети в матричной форме и в аналитическом виде при задании нагрузок в токах.

1. Матричная форма записи:

Запишем первый закон Кирхгофа в матричной форме: ,

где - вектор-столбец искомых токов ветвей;

-- вектор-столбец задающих токов узлов.

Токи ветвей можно найти как:

где -матрица падений напряжений в ветвях,

-матрица узловых проводимостей.

.

где - матрица падений напряжения в узлах относительно БУ.

Полученные уравнения подставим в первый закон Кирхгофа:

Обозначив ,

где матрица собственных и взаимных узловых проводимостей, получим:

- система узловых уравнений в матричной форме.

2. Аналитическая форма записи.

,

где -собственные проводимости узлов,

-взаимные проводимости узлов.

-ток нагрузки узла,

- напряжение балансирующего узла.

В результате записи уравнений для всех узлов, получим аналитическую форму записи:

Решив полученную систему относительно U получим значения напряжений в узлах сети.

1.5 Составление контурных уравнений установившегося режима электрической сети на основе 2-го закона кирхгофа в матричной форме и в аналитическом виде при задании нагрузок в токах.

1. Матричная форма записи:

Запишем первый закон Кирхгофа в матричной форме: ,

Матрицу M, I представим в виде двух матриц :

Запишем второй закон Кирхгофа в матричной форме:

Из первого и второго закона получим:

- контурное уравнение в матричной форме.

2. Аналитическая форма записи.