page 13
• Kirchoff’s Voltage Law: “The sum of all voltages about a closed loop in a circuit is equal to zero” - Each element will have a voltage (potential) between nodes. If any two points on the closed loop are chosen, and different paths chosen between them, the potentials must be equal or current will flow in a loop indefinately (Note: this would be perpetual motion).
3.1.1 Simple Applications of Kirchoff’s Laws
3.1.1.1 - Parallel Resistors
• Let’s consider one on the most common electrical calculations - that for resistors in parallel. We want to find the equivalent resistance for the network of resistors shown.
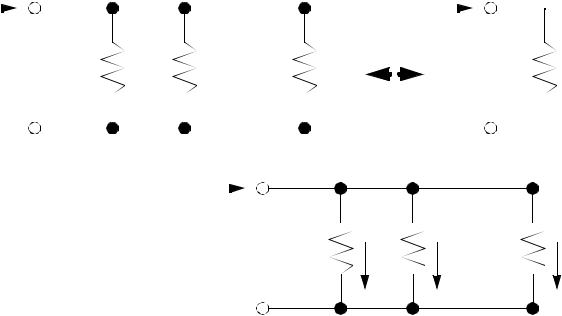
page 14
I |
|
|
|
|
|
I |
|||||
|
+ |
|
|
|
|
|
+ |
Rp |
|||
|
|
|
R1 |
R2 |
Rn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
V |
|
|
|
|
|
|
V |
||
|
|
|
|
|
|
|
|
||||
- |
|
|
|
- |
|
||||||
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
First we can define cur- |
I |
rents in each branch of |
|
the circuit. Also recog- |
|
nize that the potential |
|
voltage across each |
|
resistor will be V. |
|
+
R1 |
R2 |
Rn |
V
I1 
I2 
In
-
Now, consider the sum of the currents in and out of the upper conductor,
∑ I = I – I1 – I2 – … – In = 0
The current through each resistor is simple to calculate, so if we add the current through the resistors, and then relate the expression to Rp, the equation becomes,
I – |
-----V – -----V – … |
– |
-----V = 0 |
|
|
|
||||||
|
|
R1 |
R 2 |
|
|
Rn |
|
|
|
|
||
|
I |
= |
|
1 |
+ |
1 |
+ … |
+ |
1 |
= |
1 |
|
-- |
|
----- |
R-----2 |
R-----n |
----- |
|||||||
|
V |
|
R 1 |
|
|
|
|
|
Rp |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Rp |
= |
|
|
|
|
1 |
|
|
|
|
|
|
------------------------------------------- 1 |
+ |
1 |
+ … |
+ |
1 |
|
|
|
|||
|
|
|
----- ----- |
----- |
R2 |
Rn |
|
|
|
|||
|
|
|
|
R 1 |
|
|
|
|
|
|
||
3.1.1.2 - Series Resistors
• Now consider another problem with series resistors. We can use Kirchoff’s voltage law to sum the voltages in the circuit loop. In this case the input voltage is a voltage rise, and the resistors are voltage drops (the signs will be opposite).