4.1.6. Методы исследования функции классического анализа наиболее известны

для решения несложных оптимальных задач. Обычно областью их использование являются задачи с известным аналитическим выражением критерия оптимальности R и аналитическим выражением, как для производных вида dR/dX , так и частных производных непрерывной функции многих переменных R = R(х₁, х₂,... х_n). Экстремальные решения оптимальной зада-чи, крайне редко удается лишить аналитическим путем, в связи с чем применяют вычисли-тельные машины.

Решение задачи оптимизации существенно осложняется, когда критерий оптималь-ности является функцией нескольких независимых переменных, даже при известном анали-тическом выражении этой функции. Наибольшее же трудности возникают при отсутствии непрерывности у всех или некоторых производной оптимизируемой функции. В последнем случае для решения оптимальной задачи целесообразно использовать методы нелинейного программирования.

4.1.7. Метод множителей Лагранжа применяют для решения задач такого же класса сложности, как и в обычных методах исследования функций, но при наличии ограничений типа равенств на независимые переменные.

Методы можно применять для решения задач оптимизации объектов с распределен-ными параметрами и задач динамической оптимизации. Здесь вместо решения системы конечных уравнений для отыскания оптимума необходимо интегрировать систему диф-ференциальных уравнений. Множители Лагранжа используют так же в качестве вспомога-тельного средства при решении задач с ограничением типа равенств в вариационном исчи-слении и динамическом программировании. Следует особо подчеркнуть, что метод множи-теля Лагранжа позволяют найти лишь необходимые условия существования условного экс-тремума для непрерывных функций, имеющих к тому же непрерывные производные.

Полученные в результате решения значения неизвестных X_i должны быть проверены на экстремум с помощью анализа производных более высокого порядка или другими методами.

4.1.8. Методы вариационного исчисления

Оптимальные задачи, когда решение представляется не как совокупность значения конечного числа переменных, а как совокупность функции, вид которых заранее не известен, составляют сущность вариационного исчисления. Вариационное исчисление применяется для оптимизации математически описанных процессов.

При статистической оптимизации процессов с распределенными параметрами или в задах динамических оптимизации. Вариационные методы позволяют в этом случае свести решение оптимальной задачи к интегрированию системы дифференциальных уравнений Эйлера.

4.2. Методы детерминированного и случайного поиска

Различие указанных методов (рис.4.2) заключается в определении стратегии поиска направленного движения в n-мерном пространстве к оптимуму.

По этому признаку их можно классифицировать на методы и пассивного и направлен-ного поиска.

Последние, в свою очередь, делятся на одноэтапные (градиентные, случайного поиска) и многоэтапные (метод поочерёдного изменения переменных) (рис.4.3).

Рис. 4.3. Классификация поисковых методов

4.2.1. В основу градиентных методов поиска положены вычисление и анализ произ-водных целевой функции R(х). Если зависимость R(х) нельзя записать в явном или анали-тическом виде, то единственным способом определения производных R(х) является приме-нение численного метода.

В методе градиента используется градиент целевой функции. И поскольку направ-ление градиента в каждой точке совпадает с направлением наибыстрейшего изменения целевой функции, то локально наилучшим является градиентное направление при максими-зации или антиградиентное - при минимизации. Поиск оптимума производится в два этапа. На первом этапе находятся значения частных производных по всем независимым направ-лениям, которые определяют направление градиента в рассматриваемой точке. На втором этапе осуществляется шаг в выбранном направлении. При выполнении шага одновременно

изменяются значения всех независимых переменных, каждая из них получает приращение, пропорциональное соответствующей градиента по данной оси. В методе градиента важной задачей является выбор стратегии изменения шага. Поскольку после каждого шага прихо-дится находить производные целевой функции по «n» независимым переменным, при слиш-ком малом шаге движение к оптимуму будет долгим из-за необходимости расчета целевой

функции в очень многих точках. Напротив, если шаг выбран слишком большим, то в районе оптимума может возникнуть "рыскание", которое не затухнет, либо затухнет очень медленно. Целесообразно поэтому применять алгоритм градиентного поиска, в котором величина шага меняется автоматически в соответствии с изменением абсолютной величины градиента.

Достоинством этого алгоритма является возможность увеличения и уменьшения в процессе поиска. Момент окончания поиска определяется по выполнению предварительно заданных условий нахождения целевой функции в окрестности экстремальной точки (рис.4.4).

Рис.4.4. Характер движения к оптимуму методом градиента с малым шагом

Метод релаксации заключаются в отыскании осевого направления, вдоль которого функция цели изменяется наиболее быстро. Осевому направлению соответствует наибольшая по модулю производная. В случае минимизации движение совпадает с направлением оси (знак производной отрицательный) и шаги делаются до тех пор, пока не будет получено минимальное значение по выбранному осевому направлению. После чего вновь определя-ются производные по всем переменным за исключением той, по которой осуществляется

спуск, и снова выбирается осевое направление скорейшего убывания функции цели, по которому производятся дальнейшие шаги. Критерием окончания поиска оптимума является достижение такой точки, из которой по любому осевому направлению дальнейшего убывания функции цели не происходит (рис.4.5). Хотя метод релаксации обладает определенными достоинствами перед методом градиента, поскольку при спуске вдоль выбранного осевого направления не требуется вычисления производных, однако движение происходит все же не в оптимальном направлении, т.к. градиент в данном случае не совпадает с осевым направле-нием.

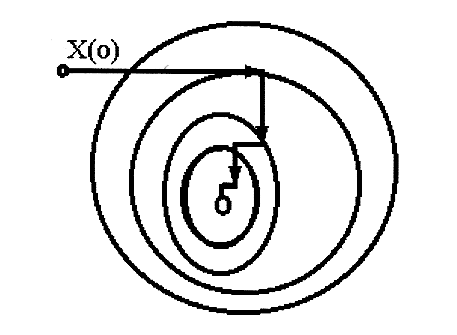
Рис.4.5 Характер движения к оптимуму в методе релаксации

В методе наискорейшего спуска нашло сочетание основных идей и методов релак-сации и градиента. Суть метода заключается в том, что после определения в начальной точке градиента оптимизируемой функцией направление движения поиска сохраняется неизмен-ным до тех пор, пока в этом направлении не будет найден минимум. После чего вычисляется градиент и определяется новое направление поиска. Данный метод является более выгодным из-за сокращения объема вычисления, особенно вдали от оптимума. Вблизи оптимума на-

правление градиента меняется резко, поэтому указанный метод автоматически переходит в метод градиента. Важной особенностью наискорейшего спуска (рис.4.6) является то, что при его применении каждое новое направление движения к оптимуму ортогонально предшест-вующему.

Рис.4.6. Характер движения к оптимуму методом наискорейшего спуска

Это объясняется тем, что движение в одном направлении производится до тех пор, пока оно не окажется касательным к линии постоянного уровня.

Метод "тяжелого шарика" в отличие от ранее рассмотренных может быть исполь-зован в задачах с целевыми функциями, имеющими несколько локальных экстремумов и характеризуется в этом смысле как метод поиска глобального экстремума.

К недостаткам градиентных методов следует отнести то, что для определения

направления движения требуется вычислить значение производной от функции по каждому параметру.

Вычисление производных может быть неточным из-за разнородности параметров, по которым выполняется оптимизация. Поэтому все параметры приводят к безразмерному виду. Поверхность отклика может оказаться такой, что придется часто изменять направление движения, а это приводит к значительным затратам времени при обращении к математиче-ской модели

Безградиентные методы детерминированного поиска используют процесс

поиска информации, получаемую не при анализе производных, а от сравнения величины критерия оптимальности в результате выполнения очередного шага.

Некоторые из этих методов целесообразно применять в сочетании с градиентными

методами, что позволяет иногда довольно эффективные алгоритмы для решения задач нелинейного программирования. Безградиентные методы, кроме того, по характеру наиболее пригодны для оптимизации действующих промышленных и лабораторных установок при отсутствии математического описания объекта оптимизации.

В рассматриваемых методах применяют одномерный и многомерный поиск. Одномер-ный поиск экстремума функции одной переменной часто используют не только как самостоя-ельный метод оптимизации, но и как вспомогательный (например, при спуске по направле-нию) в многомерных методах оптимизации. В число методов одномерного поиска относятся:

1) метод локализации функции одной переменной;

2) метод золотого сечения.

Существо этих методов состоит в определении интервала, где находится экстремум одной переменной. Поскольку точность метода "золотого сечения" (рис.4.7) на порядок выше, то остановимся на нем несколько подробнее. Допустим, что задача состоит в опре-делении положения экстремума функции одной переменной на интервале [А, В]. "Золотым сечением" Z называют деление отрезка на две части таким образом, чтобы отношение длины меньшего отрезка АС (см. рис.4.7) к длине всего интервала АВ было равно 0,38. При исполь-зовании этого метода имеется возможность с помощью одного вычисления на каждом

этапе локализовать положение экстремума Т2 =1 - Z(0,62 от длины исходного). На рис.4.7 этому соответствует отношение АС/АВ=ВВ/СВ=Т1=0,38.

Рис. 4.7. Одномерный поиск методом "золотого сечения"

Метод поочерёдного изменения переменных, называемый также методом Гаусса- Зейделя, относится к методам многоэтапного направленного поиска и по существу аналогичен методу релаксации. Отличие в том, что не определяется новое направление с помощью производных, а поочередно изменяются независимые переменные, чтобы по каждой из них достигалось экстремальное значение целевой функции. Стратегия поиска минимума по каждой перемен-ной может быть любая, целесообразно использовать здесь и методы поиска экстремума

функции одной переменной. Простота и сравнительно небольшой объём вычислений, необ-ходимых для его реализации, обусловили его распространение в системах автоматического поиска оптимума функции цели, поэтому рассмотрим некоторые аспекты его практического применения.

Пусть требуется найти минимум функции трех переменных А,В,С. Каждая

переменная определена на интервалах: [А1, А2], [В1, В2], [С1, С2]. Методом "золотого сечения" осуществим поочерёдно минимизацию целевой функции по каждой переменной, которые примут соответственно значения АМ1, ВМ1, СМ1. Получив первый приближённый минимум, повторяют поиск по каждой переменной и, если координаты точки минимума функции цели не изменились, то поиск заканчивают. В качестве критерия минимизация принята улучшенная квадратичная оценка из тех соображений, что в отличие от обычных

интегральных оценок в ней накладываются ограничения не только на величину отклонения х, но также и на скорость отклонения х.

Улучшенная квадратичная интегральная оценка имеет вид

(4.6)

где Т - некоторая постоянная времени (экстремаль).

Рис. 4.8. к методу улучшенной квадратичной оценки

1 - реальный переходной процесс; 2 - оптимальный переходной процесс

Минимизация целевой функции по (4.6) позволяет приблизить переходный процесс к экспоненте (рис.4.8) с заданной постоянной времени Т, которая носит название экстремали. Выбор параметров системы по заданной оценке приводит к меньшей колебательности пере-ходных процессов по сравнению с обычной квадратичной интегральной оценкой. При мно-гомерном поиске по методу Гаусса - Зейделя выполняется сравнение координат MINI и MIN2 по каждой переменной. Если это отклонение меньше или равно шагу поиска по каждой пере-менной, то поиск заканчивается с выводом значений координат и целевой функции. В про-тивном случае процесс оптимизации повторяется. Функция цели вычисляется в процессе расчета переходного процесса. За один такт квантования по времени вычисляется ошибка (отклонение) и ее производная. Отклонение находится как разность между установившимся значением, которое определяется путем деления свободных членов числителя и знаменателя передаточной функции, и рассчитанным на данном шаге значением переходного

процесса, как это показано на рис.4.9.

Рис. 4.9. Вычисление улучшенной квадратичной интегральной оценки

Значение интегральной оценки на каждом шаге расчёта определяют по формуле

(4.7)

где τ = 0,618.

Величина интегральной оценки за весь переходный процесса находится как

(4.8)

где N- количество шагов расчета переходного процесса.

В завершение анализа прямых методов решения оптимальных задач остановимся

на группе методов случайного поиска. Основная идея этих методов, заключается в том, чтобы перебором случайных совокупностей значений независимых переменных найти оптимум целевой функции или направления движения к нему. Общим для всех методом случайного поиска является применение случайных чисел в процессе поиска, и что относятся они к одноэтапным методам направленного поиска.

При использовании слепого поиска в допустимой области изменения независимых

переменных случайным образом выбирается точка, в которой вычисляется значение целевой функции. Далее аналогично выбирается другая точка, где также рассчитывается функция цели и сравнивается с полученным ранее. Если новое значение функции цели оказывается меньше (больше) предыдущего, то это значение запоминается вместе с координатами точки, где оно было вычислено. Затем продолжается выборка случайных точек и сравнение значе-ний критерия оптимальности в этих точках с уже найденными точками. Каждый раз, когда получается меньшее значение целевой функции, оно запоминается вместе с соответству-ющими координатами, после чего продолжается поиск лучшего приближения к оптимуму.

В соответствии с методом случайных направлений из некоторой точки Х^к в пространстве параметров делается несколько пробных шагов в случайных направлениях

(рис.4.10). Для практических расчётов число шагов в серии часто принимается равным

Рис. 4.10. Метод случайных направлений

размерности решаемой задачи m приращения функции цели, сравнивают друг с другом и определяют направления, в котором это улучшение оказалось наибольшим. При этом коор-динаты новой изображающей точки в пространстве параметров определяется по формуле

(4-9)

где - проекция наиболее удачного пробного шага на ось Х_i;

- величина рабочего шага;

- значение пробного шага.

Критерием окончания поиска служит минимальный размер шага Н_min, которым и задается точность определения оптимума.

Метод случайных направлений с обратным шагом представляет собой улучшение алгоритма, описанного выше. Отличительной его особенностью является то, что при неудач-ном шаге из точки сразу производится шаг в обратном направлении. При достаточном удалении от оптимума такая стратегия оказывается весьма эффективной. Если и обратный шаг оказался неудачным, то можно либо сделать новый случайный шаг из точки Х^к , либо перейти к поиску с уменьшенным размером шага из этой точки.

Метод случайных направлений с линейным пересчетом может использоваться,

если кривизна оптимизируемой функции относительно не высока и в пределах полного шага поиска изменение целевой функции можно аппроксимировать линейной формой.

Метод спуска "с наказанием случайностью" по существу представляет собой аналог метода наискорейшего спуска с той лишь разницей, что направление спуска выби-рается случайным образом. Указанный метод целесообразно использовать тогда, когда для нахождения значений целевой функции не требуется больших вычислительных затрат.