1.5.3. Производящая функция для чисел Фибоначчи

Числа Фибоначчи – это элементы числовой последовательности, в которой каждый последующий элемент равен сумме двух предыдущих. Т.е. последовательность чисел Фибоначчи задается рекуррентным уравнением:

Воспользуемся понятием производящей функции для выражения общего члена чисел Фибоначчи.

Возьмем в качестве последовательности базисных функций .

Ряд

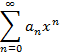
сходится при и определяет производящую функцию

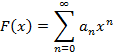
Помножив данное выражение на xи на, получим:

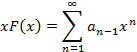
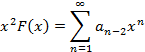
Сложив эти два выражения имеем:

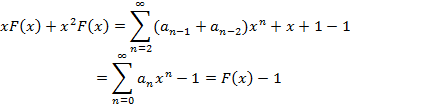
Следовательно

.

Отсюда получается явный вид производящей функции

Корни знаменателя определяются из уравнения

Разложим F(x)на элементарные дроби, т.е.

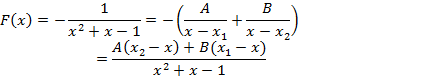
Т.е. получим

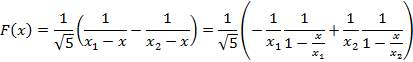
Рассмотрим сумму бесконечно убывающих геометрических прогрессий

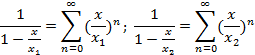
При

Следовательно

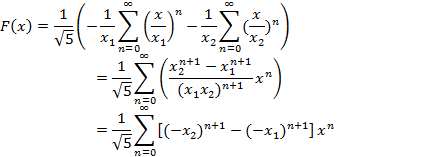
Отсюда

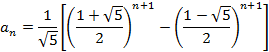
1.6. Z - преобразование

1.6.1. Определение z– преобразования

При анализе и синтезе дискретных устройств широко используется Z–преобразование, играющее по отношению к дискретным сигналам такую же роль, как интегральное преобразование Фурье и Лапласа по отношению к непрерывным сигналам. Рассмотрим основы теории этого функционального преобразования и некоторые его свойства.

Одностороннее Z-преобразование последовательностиx(n) определяется формулой:

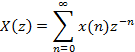
где z – комплексная переменная , а n интерпретируется как дискретное время. Из этого следует, что Z- преобразование представляет собой частный случай производящей функции в которой в качестве базисной используется последовательность

Рассмотрим ряд примеров.

Пример 1. НайтиZ-преобразование единичного импульса.

Решение. Т.к.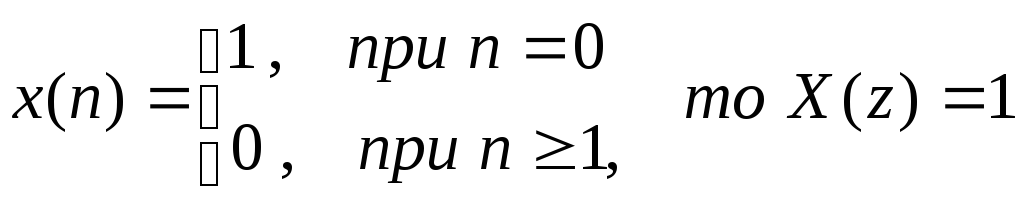

Пример 2. Найти Z-преобразование единичного сигнала

Решение. В данном случае, для

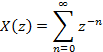
Данный ряд представляет собой бесконечную сумму убывающей геометрической последовательности знаменатель который . Следовательно

сходится при

Пример 3. НайтиZ– преобразование экспоненциальной последовательности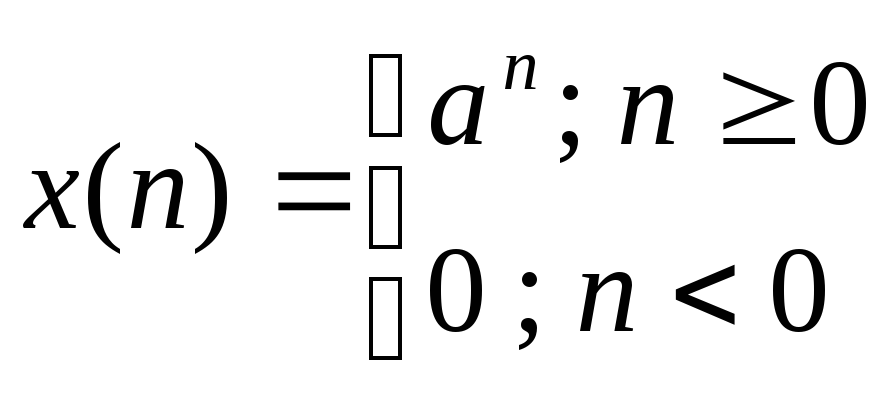

Решение. ВычисляяZ-преобразование, получим

сходится при

1.6.2. Обратное преобразование

Очень важно уметь переходить не только от последовательности к ее Z– преобразованию, но и обратно от Z–преобразования к последовательности. Последний переход формально определяется соотношением

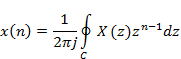
В правой части этого равенства стоит контурный интеграл в z-плоскости по любому замкнутому контуру в области сходимости, охватывающему начало координат.

Обратное Z-преобразование можно найти несколькими способами:

1. Прямым вычислением контурного интеграла с использованием теоремы о вычетах

2. Разложением 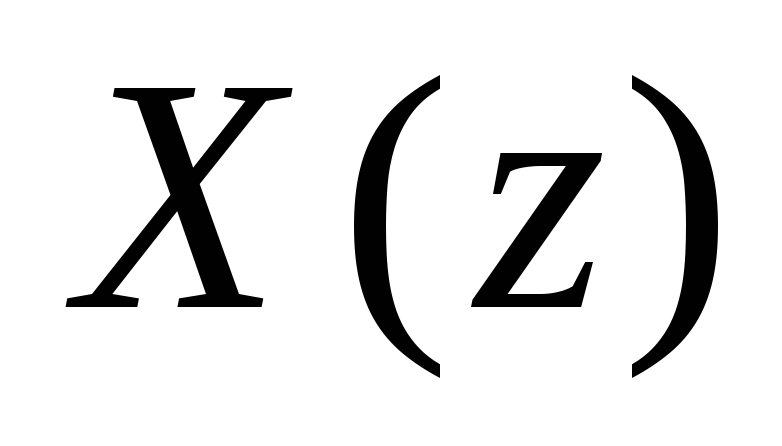на простые дроби

3. Обычным делителем числителя 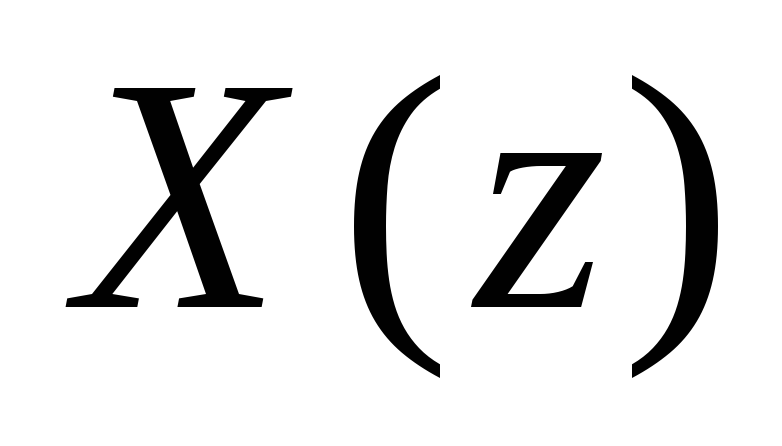на его знаменатель.

4. Разложением в степенной ряд.

Мы ограничимся рассмотрением двух первых из них.

Первый способ основан на известной теореме из курса теории функций комплексного переменного, позволяющего вычислить контурный интеграл через вычеты.

Рассмотрим пример 4, в котором

В этом случае мы имеем простой полюс в точке . Следовательно:.

При использовании второго способа Z-преобразование записывается в виде суммы простых дробей

Т.к. каждое слагаемое имеет обратноеZ-преобразование вида, получим

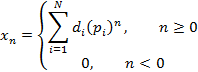
Например, рассмотрим выражение

Его можно записать в виде

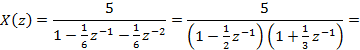
В результате получаем

1.6.3. СвойстваZ-преобразования

1) Линейности

2) Задержки

где – функция единичного скачка

3) Умножения на экспоненту

4) Умножения наn

5) Опережающего сдвига

6) Свертки

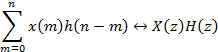
Указанные свойства упрощают получение преобразований и их обращений.