3.2. Нечеткие отношения

Нечётким отношением на множественазываетсянечеткое подмножество декартова произведенияхарактеризующиеся функциями принадлежностиЗначениепонимаются как степень выполнения отношения

Если Xконечно, то функция принадлежностипредставляет собой квадратную матрицэлемент который означает степень выполнения отношения

Для нечеткого отношения определяется множество уровня:

Матрица множества уровня получается заменой матрицы нечеткого отношенияRединицами всех элементов, значения которых не меньшеа нулями все остальные элементы.

Для уровневых множеств нечетких отношений справедлива теорема от декомпозиции:

Любое нечеткое отношение Rможет быть представлено в форме:

Где

Запись обозначает, что все элементы обычного отношенияумножаются на

Пример

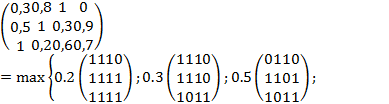
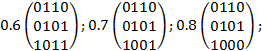
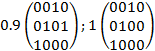
Носителем нечеткого отношения Rназывается обычное отношениетакое, что

Обычное отношение, ближайшее к данному нечеткому отношению определяется следующим образом:

На нечетких отношениях вводятся отношения включения и равенства, а также операции дополнения, пересечения и объединения с помощью тех же формул, что и для нечетких множеств.

Кроме того для нечетких отношений А и В, определенных на утиверсумеХ, вводится операция (максимальной) композиции.

.

Например

А В АВ

Свойства нечетких отношений

Нечеткое отношение Rназывается:

1. Рефлексивным, если

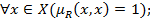
2. Симметричным, если

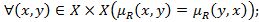
3. Антисимметричным, если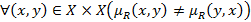или

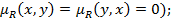
4. Несимметрично, если

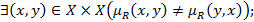
5. Совершенно антисимметричным, если

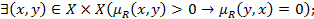
6. (максимально) транзитивным, если

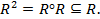
Транзитивным замыканием нечетного бинарного отношения RназываетсяотношениеЕслито

Виды нечетких отношений

Нечеткие отношения предпорядка– это то, которое обладает свойствами транзитивности и рефлективности.

Нечеткое отношение нестрогого порядка– это то, которое обладает свойствами транзитивности, антисимметричности и рефлективности.

Нечеткое отношение строгого порядка– транзитивное, антисимметричное и антирефлексивное отношение.

Рефлексивное и симметричное отношение называются отношениями сходства.

Нечеткое отношение обладающее свойствами рефлективности, симметричности и транзитивности называются отношениями подобия (нечетким отношением эквивалентности)

3.3. Нечеткая логика

Нечетким высказываниемназывается повествовательное предложение А, степень четности которого принимает значение на отрезке.

Если то, о чем говорится в предложении не определено, то это предложение называется высказывательной функцией или предикатом. Аргументом предиката являются предметные переменные.Нечеткой предметной переменнойназывается переменная, степень истинности которой принадлежит отрезку [0.1].

Как правило, нечеткой предметной переменной является лингвистическая переменная, значениями которой являются слова и словосочетания естественного языка. Лингвистическая переменная служит для качественного писания явления, факты или события. Множество лингвистических переменных называютсятерм-множествоми обозначаютсяT(x).

Нечеткие высказывания бывают простыми и сложными. Для формирования сложных высказываний используются логические связки отрицания, конъюнкции, дизъюнкции, импликации и эквивалентным. В результате этого формируются нечеткие логические формулы.

Степень истинности сложного высказывания определяется по следующий правилам:

В логике нечетких высказываний операция импликации, отличается от классической. Чаще всего она используется в виде: «Если А, то В, иначе С». Такое высказывание определяется через нечеткое отншение на декартовом произведении множеств, т.е.Истинность такого высказывания определяется по формуле.

В частном случае, когда