2.4. Автоматные функции и эксперименты с автоматами

2.4.1. Понятие ограниченной детерминированной функции\

Пусть даны— входной алфавит и— выходной алфавит. Обозначимикак множества все возможных последовательностей в алфавитахAиBсоответственно.

Определение 1. Отображение→называетсядетерминированной функцией, еслиb(t)для любогоt=1,2,… однозначно определяется поa(1),a(2),…,a(t).

Функция такая, что

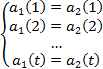будет g-функцией, если, тои если,то.

Определение 2. Пусть заданаg-функция→. Рассмотрим произвольное входное слово.Определим функциюследующим образом: пустьa(1),a(2),…,a(t)— произвольная входная последовательность. Рассмотрим. Тогда положивпри этом называетсяостаточной функциейφ по слову.

Определение 3. Детерминированная функция→называетсяограниченно-детерминированной функцией, если у нее имеется лишь конечное число различных остаточных функций. Рассмотрим автомат (A,S,B,φ,,) гдеA,S,B— конечные алфавиты (входной, выходной и состояния),- переходная функция,- выходная,- начальное состояние.

Входом автомата служит последовательность a(1),a(2),…,a(t)ϵ(конечная или бесконечная), выходом автомата служит последовательность, при этом автомат задаетсясистемой канонических уравнений:

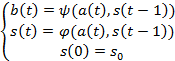
Определение 4. Отображение→называетсяавтоматной функцией, если существует автомат, который реализует это отображение. Справедливо утверждение. Справедливоутверждение: функция является автоматной тогда и только тогда, когда она ограниченно детерминированная.

Пример:Пусть, а система канонических уравнений выглядит следующим образом:

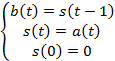
Такой автомат осуществляет отображение и называетсяединичной задержкой.

2.4.2. Моделирование автоматной функции с помощью схемы из функциональных элементов и задержки

Определение.Схемой из функциональных элементов и элементов задержки(СФЭЗ) называется схема, содержащая элементы некоторой функциональной системы, к функции которой добавлены элементы, реализующие функцию единичной задержки. В СФЭЗ допускаются ориентированные циклы, но любой ориентированный цикл должен проходить хотя бы через одну задержку.

Теорема 1. Схема из функциональных элементов и задержки осуществляет автоматное отображение.

Определение. Пусть автоматная функция отображает последовательность конечного базиса в последовательность конечного базиса. Пусть СФЭЗΣ осуществляет преобразование последовательностей булевых векторов длиныnв последовательность с булевыми векторами длиныm. Говорят, чтоΣмоделируетφ, если существуют отображения (кодирования)и, которые сопоставляют разным элементам алфавита разные векторы. Эти отображения обладают свойством: для любой последовательностив алфавите, если

, где.

Теорема 2. Для любой автоматной функции существует моделирующая ее СФЭЗ в функционально полной системе, состоящая из элементов дизъюнкции, конъюнкции, отрицания, а также элемента задержки.

2.4.3. Эксперименты с автоматами

Эксперимент с автоматами— это способ получений информации о внутренней структуре автоматов по их поведению. Основная задача экспериментов — получить сведения о строении автомата путем наблюдения его реакции на внешние воздействия.

Рассмотрим автоматы, в которых не выделены начальные состояния. В этом случае автомат задается пятеркой(A,S,B,φ,).обозначается множество всех конечных слов в алфавите. Пусть автомат (A,S,B,φ,)находится в состоянии и на вход подаются слова. Тогда на выходе будет некоторое словои после подачи всего слова автомат оказывается в состоянии. Раcширяя функциииψ, положим.

Определение 1.Два состоянияиавтомата (A,S,B,φ,)называются отличимыми, если существует входное словотакое, что. При этом словоназывается экспериментом, отличающим оти, а длину словаI() называют длиной эксперимента.

Теорема 3 (Мури). Если в автомате (A,S,B,φ,)состоянияиотличимы и |S|=r, то существует эксперимент, отличающийидлины.

Определение 2. Пусть два автоматаи, т.е. автоматы, имеющие одинаковые входной и выходные алфавиты. Пустьи. Говорят, что экспериментотличает состояния, если.

Теорема 4. Даны два автоматаипричем

и. Тогда, если состоянияиотличимы, то существует отличающий их эксперимент, длины которого.