2. Теория автоматов

2.1. Понятие конечного автомата

2.1.1. Общие сведения о конечных автоматах

Данный раздел посвящен математическому описанию работы цифровых вычислительных машин (ЦВМ) с помощью понятий множества, отношения, функции и графа. При этом из рассмотрения исключаются аналоговые вычислительные машины, состояние которых меняется непрерывно. Не рассматриваются также гибридные устройства, сочетающие цифровые и аналоговые компоненты. С математической точки зрения, все многообразие ЦВМ можно отнести к одному классу конечных автоматов.

Они обладают следующими свойствами:

1. Любая ЦВМ состоит из конечного числа элементов, каждый из которых в любой момент времени может находиться лишь в одном из конечного числа устойчивых состояний. Поэтому вся машина в целом имеет конечное множество состояний.

2. Любая ЦВМ работает последовательно, то есть ее операции синхронизированы сигналами тщательно настроенных электронных часов. В связи с этим состояние машины меняется в четкой последовательности.

3. ЦВМ является детерминированным устройством. Это значит, что при наличии полной информации о внутренних состояниях всех элементов машины и всех ее входов следующее состояние машины определяется однозначно.

ЦВМ делятся на универсальные и специализированные. В теории конечных автоматов анализируются универсальные машины, которые используются для любых целей.

С функциональной точки зрения современные ЦВМ состоят из 5 типов устройств:

1) устройство ввода;

2) устройство памяти;

3) арифметико-логическое устройство;

4) устройство управления;

5) устройство вывода.

ЦВМ конструируются на электронных схемах, имеющих два устойчивых состояния. Основная причина – технологическая. Но в этом случае возрастает также надежность электронных схем. Это связано с тем, что небольшие отклонения характеристик электронных схем не отражаются на работе всего устройства в целом.

Таким образом, типичный сигнал в элементах ЦВМ имеет следующий вид

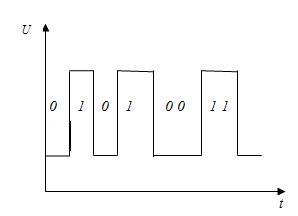
При этом единицей кодируется сигнал более высокого уровня, а нулём – более низкого. Или более точно, устанавливается некоторое пороговое значение сигнала и далее сигналы выше порога кодируются 1, а ниже – 0. Таким образом, не вникая в дальнейшие особенности работы электронных схем, отметим, что сигналы в таких устройствах двузначны. Это значит, что переменные, используемые для их описания, принимают только два значения. Это же замечания относится и к материальным носителям информации и к преобразователям сигналов. В результате состояние любой ЦВМ, имеющей конечное число rдвоичных элементов математически может быть описано следующим образом.

Нумеруются элементы ЭВМ, затем с каждым устойчивым состоянием связывается вектор

.

При этом координате приписывается значение 1, если-й элемент находится в единичном состоянии, и 0, если-й элемент находится в нулевом состоянии.

2.1.2. Абстрактное определение конечного автомата

Абстрактным описанием ЦВМ служит математическое понятие конечного автомата.

Определение.Конечным автоматомназывается набор из пяти объектов:

, где

- конечный список входных символов (входной алфавит);

- список выходных символов (выходной алфавит);

- множество внутренних состояний;

- функция переходав следующее состояние;

- функция выхода.

Таким образом, конечный автомат математически описывается тремя множествами и двумя функциями. Его действие состоит в том, что он считывает последовательность входных символов (программу), а затем печатает последовательность выходных символов. Это действие происходит последовательно, а именно, конечный автомат, находящийся во внутреннем состоянии считывает входной символ. Функцияна парепринимает значение, которое печатается в качестве выходного символа. Функцияна той же парепринимает значение, которое является следующим внутренним значением автомата. Далее автомат считывает новый входной символ, печатает выходной, переходит в следующее состояние и так далее. Эту последовательность работы можно наглядно представить в следующем виде.

Вопределении конечного автомата предполагается, что функции и всюду определены. Такое описание автомата называетсяполным.

Пример. Автоматимеет входной алфавит, выходной алфавит, множество внутренних состояний.Функции перехода и выхода задаются предписаниями:

Подадим на вход последовательность 0,1,0,1. Если автомат находился в состоянии , то считав первый символ 0, он перейдёт в состояниеи напечатает0. Считав затем 1, он перейдёт в состояниеи напечатает0. Считав следующий 0, он перейдёт в состояниеи напечатает1. Наконец, считав последний символ 1, автомат закончит работу в состоянии, печатая0. Таким образом, автомат преобразовал входной сигнал 0101 в сигнал 0010 на выходе.

Возможны следующиеспособы описания конечного автомата:

1) С помощью диаграммы состояний, которая представляет собой ориентированный граф. Вершины этого графа помечаются символами, обозначающими внутренние состояния автомата. А каждая дуга помечается упорядоченной парой символов . Первый символ есть входной символ, вызывающий переход автомата в следующее состояние. Второй символ - выходной символ, который автомат печатает. Диаграмма состояния для выше приведённого примера имеет вид.

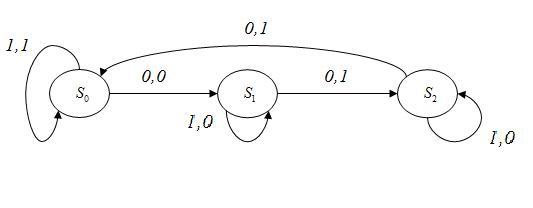
2) Второй способ описания конечного автомата - таблица состояний– это табличное представление функций и . В соответствии с примером

Текущее состояние	Следующее состояние		Выход
	0	1	0	1
			0	1
			1	0
			1	0

Оба способа описания конечного автомата имеют свои преимущества и недостатки. Таблица состояний удобна при вычислениях, а диаграмма состояний является более наглядной. В частности, по диаграмме состояний конечного автомата можно обнаружить состояния недостижимые из других состояний. Например:

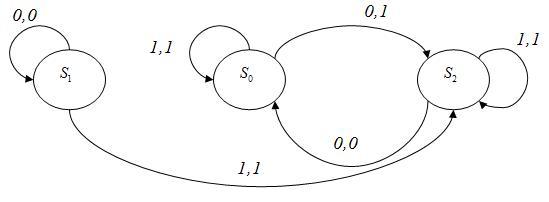
На этом рисунке показана диаграмма состояний конечного автомата, у которого состояние недостижимо, если автомат начинает работу из состоянийили.