6. Изучение вынужденных электромагнитных колебаний (Лабораторная работа №2.15)

Цель работы:исследование резонансных кривых тока и напряжения в колебательном контуре, определение добротности контура.

Теоретическое введение

Вынужденные электромагнитные колебания наблюдаются в колебательном контуре (рис.6.1), содержащем индуктивность L, емкостьCи активное сопротивлениеRпри подключении его к источнику переменной ЭДС.

. (6.1)

По второму правилу Кирхгофа: или

, (6.2)

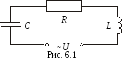где - ЭДС самоиндукции в индуктивности.

С учётом того, что I=, иξ_S= -L уравнение (6.2) принимает вид

, (6.3)

40

гдеβ = R/2L– коэффициент затухания,ω₀ = 1/√LC– частота собственных колебаний

Уравнение (6.3) представляет собой стандартное дифференциальное уравнение вынужденных электромагнитных колебаний. При установившихся колебаниях его решение можно представить в виде

. (6.4)

Тогда:

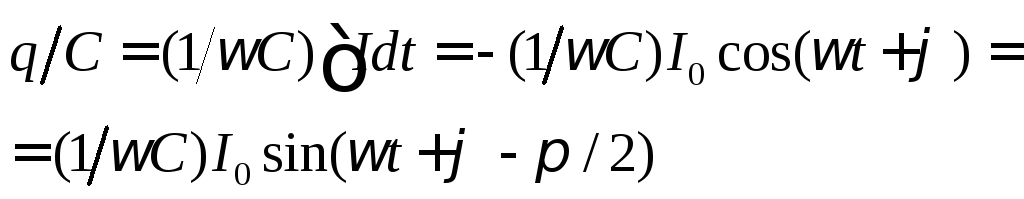
То есть, левая часть уравнении (6/2) и (6/3) есть сумма колебаний трёх напряжений одинаковой частоты на элементах контура:

на L с амплитудойU_L0 =ωLI₀, (6.5)

опережающего ток на π/2;

на Rс амплитудойU_R0 =RI₀, (6.6)

синхронного с током;

на С с амплитудой U_C0= I₀/ωC, (6.7)

отстающего от тока на π/2.

Для их сложения применяют метод векторных диаграмм, наглядно преставляя напряжения векторами (рис.6.2), модули которых равны их амплитудам, а взаимное расположение определяется фазовым углом их сдвига относительно вектора тока (рис.6.2).

Из векторной диаграммы следует закон Ома для цепей переменного тока

, (6.8)

41

определяющий амплитуду тока в контуре, и формула. определяющая угол фазового сдвига между током и напряжением:

. (6.9)

Знаменатель в (6.8) определяет полное сопротивление (импеданс) цепи переменного тока, который складывается из активного R, индуктивногоωLи емкостного 1/ωСсопротивлений. Из (6.8) видно, что амплитуда тока в контуре зависит не только от величинR,L,Cи вынуждающей ЭДСξ, но и от её циклической частотыω. Когдат.е.

, (6.10)

амплитуда тока достигает максимума I=ξ/R.Резкое возрастание тока в колебательном контуре при приближении вынуждающей частоты ω к ω₀ называется явлением резонанса.

Резонансные кривые, т.е. зависимость амплитуды колебаний от частоты вынуждающей ЭДС I_m(ω)при различных величинахRпоказаны на рис.6.3. Максимум при резонансе получается тем выше и острее, чем меньшеβ=R/2L.

42

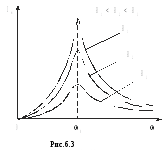
Частота резонанса тока не зависит от величины R, а частота резонанса напряжения на конденсаторе

. (6.11)

С увеличением βчастота резонанса напряжения на конденсаторе уменьшается (рис.6.4).

Резонансные свойства контура характеризует добротность Q, которое показывает, во сколько раз напряжение на конденсаторе при резонансе может превышать приложенное напряжение, т.е

.. (6.12)

При малом коэффициенте затухания ω_рез ω₀

. (6.13)

Таким образом, добротность обратно пропорциональна активному сопротивлению контура и определяет остроту резонансных кривых для силы тока в контуре. Частоты ω₁и ω₂соответствуют токуJ=J_max/√2.

43

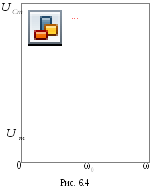
Относительная ширина резонансной кривой равна величине обратной добротности контура, т. е.

. (6.14)

Рис.6.5

44

5

Явление резонанса используют для выделения нужной составляющей из сложного напряжения, равного сумме нескольких синусоидальных напряжений. Пусть напряжение, приложенное к контуру, равно

U = U_m1cos(₁t + ₁) + U_m2cos(₂t + ₂) +…+ U_micos(_it + _i) +…+ U_mncos(_nt + _n).

Настроив контур (посредством изменения RиC) на требуемую частоту_i, можно получить на конденсаторе напряжение вQраз превышающее значение данной составляющей, в то время как напряжение, создаваемое на конденсаторе другими составляющими, будет слабым. Таким образом осуществляется, например, настройка радиоприёмника на нужную длину волны.