
2013.Термодинамика / Paskal / 2011_09_27 / 2011_09_27 / IMG_0022а60-61
.docно ниже бинодали и неравновесно выше её.
Обе
куполообразные линии - бинодаль и
спинодаль - на диаграмме
состояния
![]() (рис,
1-24)
имеют обшую точку максимума
при
(рис,
1-24)
имеют обшую точку максимума
при
![]() и
и
![]() -
критическую точку. В этой точке исчезает
различие между двумя фазами - жидкой и
газообразной Очевидно, что в критической
точке одновременно выполняются условия
-
критическую точку. В этой точке исчезает
различие между двумя фазами - жидкой и
газообразной Очевидно, что в критической
точке одновременно выполняются условия
![]() (поскольку
в критической точке исчезают
(поскольку
в критической точке исчезают![]() экстремумы
изотермы). Так как в критическую точку
выходит точка перегиба, содержащаяся
между экстремумами изотермы при
экстремумы
изотермы). Так как в критическую точку
выходит точка перегиба, содержащаяся
между экстремумами изотермы при
![]() >
то в ней .выполняется также
>
то в ней .выполняется также
![]() или
или![]()
Продолжим
анализ равновесной системы Ван-дер-Ваальса
до
получении поверхности энергии Гиббса
на трехмерном графике
![]()
Поверхность энергии Гиббса система Ван-дер-Ваальса
Из
вида графика
![]() нетрудно
определить вид графика
нетрудно
определить вид графика![]() ,
что
осуществлено на рис. 1.25 непрерывной
изотерме,
,
что
осуществлено на рис. 1.25 непрерывной
изотерме,
 (р)
соответствует
изотерма
(р)
соответствует
изотерма
![]() ,
состоящая из двух пересекающихся
ветвей,
изображающих устойчивые однофазные
равновесия. Концы этих
ветвей соединяют отрезок t
,
состоящая из двух пересекающихся
ветвей,
изображающих устойчивые однофазные
равновесия. Концы этих
ветвей соединяют отрезок t![]() ,
соответствующий
неустойчивому
участку изотермы
,
соответствующий
неустойчивому
участку изотермы
![]() Ван-дер-Ваальса.
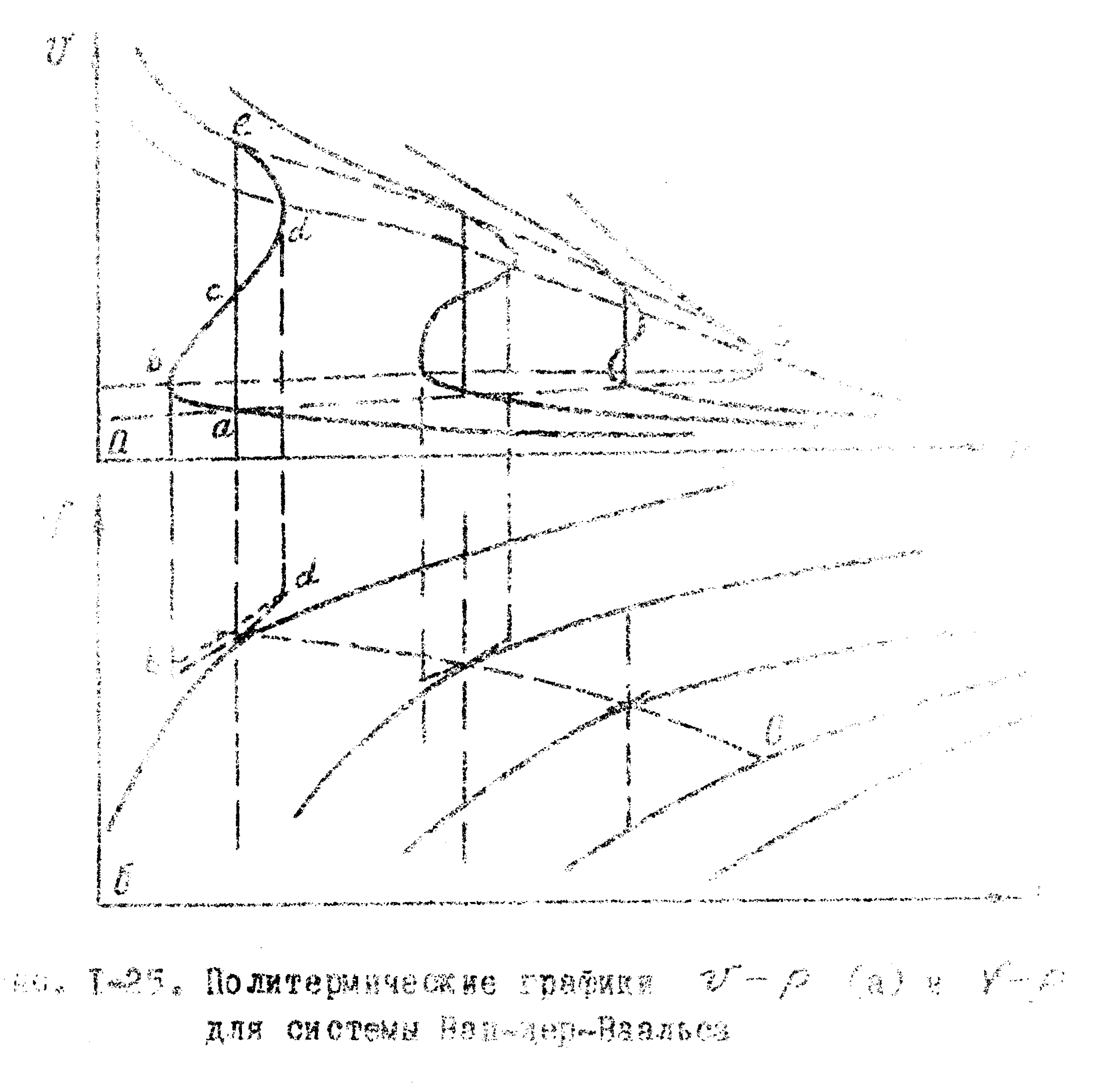
Переходя от политермического графика
V-р
к
политермическому графику
Ван-дер-Ваальса.
Переходя от политермического графика
V-р
к
политермическому графику![]() легко увидеть, что о повышением
температуры устойчивые ветви изотермы
легко увидеть, что о повышением
температуры устойчивые ветви изотермы
![]() всё
меньше
отличаются
по наклону в точке их
всё
меньше
отличаются
по наклону в точке их
пересечения
вместе с тем метастабильные участки
изотерм сокращается.
При![]() метастабильные
участки изотерм исчезают, а наклон
изотерм в точке пересечения становится
одинаковым: вместо двух
изотерм мы имеем одну. При
метастабильные
участки изотерм исчезают, а наклон
изотерм в точке пересечения становится
одинаковым: вместо двух
изотерм мы имеем одну. При
![]() в
точке слияния изотерм имеется
лишь визуально
незаметная особенность (скачкообразное
из-
в
точке слияния изотерм имеется
лишь визуально
незаметная особенность (скачкообразное
из-
мнение радиуса кривизны),
Из
политермического графика
![]() можно
теперь воспроизвести
поверхность энергии Гиббса (рис. 1-2?)
в пространстве
можно
теперь воспроизвести
поверхность энергии Гиббса (рис. 1-2?)
в пространстве
![]() Эта поверхность замечательна тем, что
о ней нельзя сказать категорически:
представляет она собой одну
поверхность
или две разные поверхности. Перемещаясь
по такой поверхности произвольным
образом, но не пересекая линию,
Эта поверхность замечательна тем, что
о ней нельзя сказать категорически:
представляет она собой одну
поверхность
или две разные поверхности. Перемещаясь
по такой поверхности произвольным
образом, но не пересекая линию,![]() ,
мы пришли бы к
выводу
о том, что остаемся в пределах одной
поверхности. Перемещение
же по любому пути, пересекающему линию
,
мы пришли бы к
выводу
о том, что остаемся в пределах одной
поверхности. Перемещение
же по любому пути, пересекающему линию![]() убедило бы
в
том, что мы имеем дело с двумя различными
поверхностями.
убедило бы
в
том, что мы имеем дело с двумя различными
поверхностями.
