2013.Термодинамика / Paskal / 2011_09_27 / 2011_09_27 / IMG_0053-123

- 123 -

Атермичные растворы

Можно доказать, что раствор, атермичкый в отноюении какого-либо -го компонента, атермичев и в отношении любого другого -го компонента, а следовательно, атериичен в целой.

Пусть =о(при всех составах). (2.3_#3)

Составим выражения типа для м.п. теплот смешения:

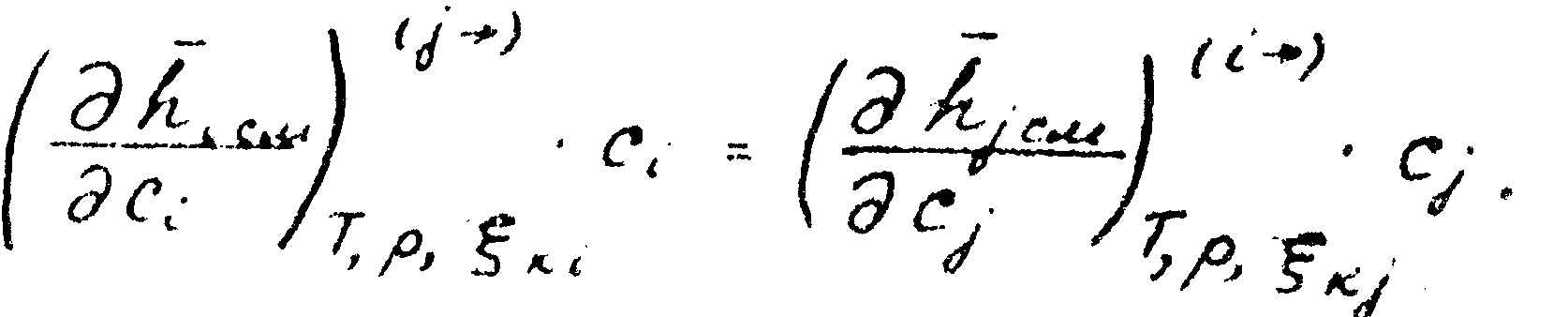(2.3.4)

Из_(2.3.3)следует

Подставляя это выражение в получим

Следовательно: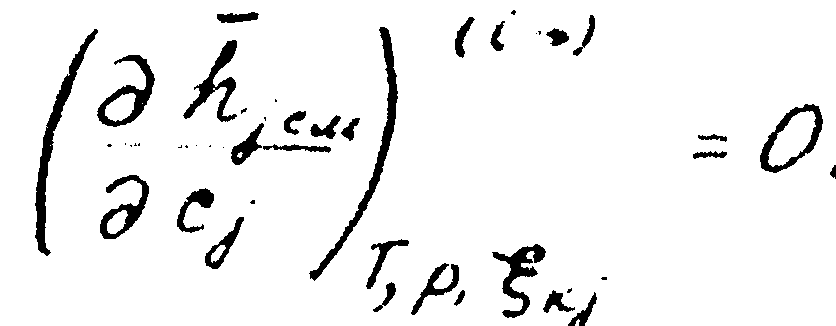

В частности, при _,поэтому при любом

, что и требовалось доказать. К экспериментальным данным доказанное сейчас положение следует применять с известной осторожностью. Одна из может быть отличной от нуля, но очень малой по абсолютной величине и невыявимой при данной точности эксперимента, в то время как другие могут оказаться существенно отличными от нуля. Следует заметить также; что в некоторой области концентраций может быть

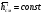тогда в этой области и , Во всей же концентрационной области не может быть_р кроме того случая, когда