2013.Термодинамика / Thermdina

Thermdina

Термодинамическое состояние твердого тела может быть определено через компоненты тензора деформации. Основным выражением теории упругости является выражение термодинамических потенциалов через компоненты тензора деформации. Упругие константы определяются через производные от этих потенциалов по компонентам деформации. Для точного описания необходимо использовать тензор конечных деформаций, который при определенных условиях переходит в тензор бесконечно малых деформаций.

Между координатами материальной точки в исходном и деформированном состоянии будем предполагать линейную связь. Это сделаем, чтобы избежать не нужных осложнений. При достаточно малых объемах среды, даже для неоднородной деформации можно принять, такое линейное соотношение. Для однородной деформации такое соотношение является точным.

Координаты

Будем использовать фиксированную ортогональную систему координат. координаты материальной точки P в естественном состоянии с нулевым напряжением и фиксированной температурой обозначаются a_i (i=1,2,3). Координаты этой же самой точки P в реальном состоянии x_i. В ряде случаев рассматривается (начальное) состояние, отличающееся от естественного состояния, и координаты точки P в этом случае обозначим X_i. Единичные векторы вдоль координатных осей e₁ , e₂,e₃.

Смещения

Компоненты вектора смещения u запишем следующим образом

u_i =x_i -a_i или (X_i-a_i) (1)

Градиент деформации

J_ik=x_i/ a_k (2)

Плотность:  - реальная плотность. ₀ - плотность в недеформированном состоянии

дельта символ

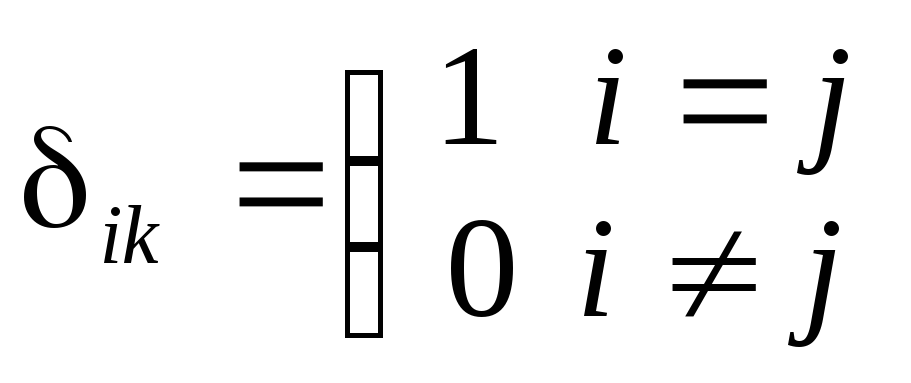
Тензор бесконечно малой деформации симметричный тензор

(3)

Тензор конечных деформаций (симметричный)

(4)

Тензор напряжений

Компоненты тензора напряжений записываются: _ij. Рассматривается единичный куб в действительном состоянии. Грани куба || координатным плоскостям. Тогда _ij. - есть i -ая компонента силы, действующая в через перпендикулярную j - ому направлению грань куба на материал куба.

Термодинамические величины

U - внутренняя энергия на единицу массы.

F - свободная энергия на единицу массы.

G -свободная энергия Гиббса на единицу массы.

S - энтропия на единицу массы.

T - абсолютная температура

Упругие коэффициенты

Адиабатические коэффициенты жесткости второго порядка

(5) U(V,S)

Изотермический коэффициент жесткости второго порядка

(6) F(V,T)

Изотермический коэффициент податливости второго порядка

(7) G(P,T)

В формулах (5) и (6) дифференцируем по компонентам тензора деформации , а в (7) по компонентам тензора напряжений.

Приведем еще изотермический коэффициент жесткости третьего порядка

(8)

Когда речь идет о коэффициенте жесткости, то рассматривается действие вызванное деформацией, т.е. деформируем на заданную величину.

Когда говорим о коэффициенте податливости, то к телу прилагаем напряжения и смотрим, какие это вызовет изменения.

При малых деформациях, между деформациями и напряжениями существует линейные связи, называемые законом Гука.

Матричные обозначения

Двойное сочетание ij (i,j=1,2,3) заменяется единственным символом от 1 до6 по следующей схеме

11  1 22  2 33  3 23,32  4 31,13  5 12,21  6 (9)

Компоненты деформации в этой записи имеют вид

₁₁ = ₁ , ₂₂ =₂ , ₃₃ = ₃ ,₂₃ =₃₂ =₄/2 (10)

Компоненты коэффициентов упругости, компоненты жесткости преобразуются непосредственно по схеме (9) а компоненты податливости следующим образом

S_ij,kl=S_m,n (1+_ij )(1+_kl)/4 ijm kln (11)

S_11,11 S₁₁ S_12,23S₁₄ S_23,23=S₄₄/4

Если среда деформируется однородно, то

x_i=a_i+_ija_j (  по j) (12)

_ij - константы. x_i - координаты в деформированном состоянии материальной точки P, которая имела в недеформированном состоянии в ортогональной системе координаты a_i.

Таким образом, смещение точки P описывается матрицей с 9-тью коэффициентами

Величина коэффициентов _ij зависит от выбора системы координат. Физические характеристики определяются 6-ю независимыми инвариантами, которые не зависят от выбора координатной системы. Сами смещение есть вектор и не зависит от выбора системы координат .

Если коэффициенты _ij -бесконечно малые, такого порядка, что их произведениями можно пренебречь, то из тензора конечных деформаций можно получить тензор бесконечно малых деформаций, который можно определить как выражением (3), так и следующим образом

(13)

где векторы e_j -материальные единичные векторы, направленные по трем координатным осям в начальном состоянии, а e_j - векторы, в которые материальные векторы переходят при деформировании

В общем случае

(14)

где векторы C_j -материальные векторы, не обязательно единичной длинны, первоначально располагавшиеся вдоль координатных осей и при деформировании переходят в векторы b_j.

При бесконечно малых деформациях объем V₀ в исходном состоянии переходит в объем V где

V=V₀(1+₁₁ +₂₂+ ₃₃) (15)

Аналогично (14) компоненты тензора конечной деформации можно определить из материальных векторов C_j и b_j.

(15)

Объем куба со сторонами единичной длинны параллельными координатным осям становится равным

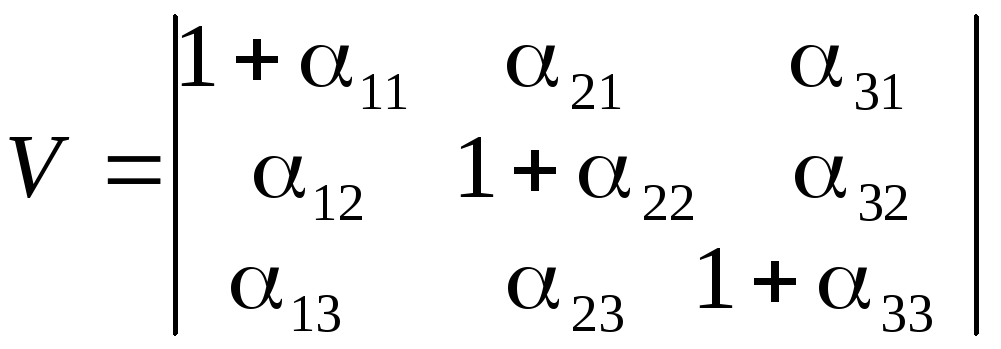
(16)

Рассмотрим некоторые соотношения подробнее

Компонента тензора бесконечно малой деформации (или для однородной) деформации

связана со смещением u_i = _ija_j следовательно

_jk = (_jk+_kj)/2 (17)

Рассмотрим один из векторов e_j, например e₁. Формула (17) дает связь между смещением и тензором деформацией.

Рассмотрим единичный материальный вектор e₁ до деформации его координаты (1,0,0) после деформации координаты (1+ ₁₁, _{21 ,} ₃₁). Координаты вектора смещения u₁=(₁₁, _{21 ,} ₃₁) . После деформации

e₂=( ₁₂, 1+_{22 ,} ₃₂) u₂==( ₁₂, _{22 ,} ₃₂)

e₃=( ₁₃, _{23 ,} 1+₃₂) u₃==( ₁₃, _{23 ,} ₃₃)

,,

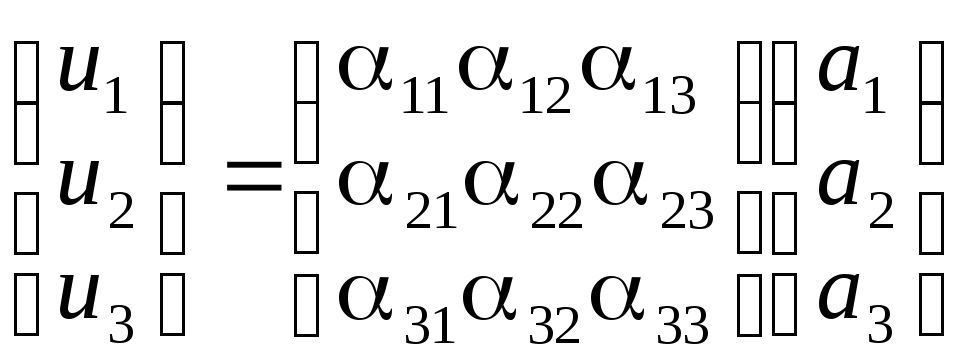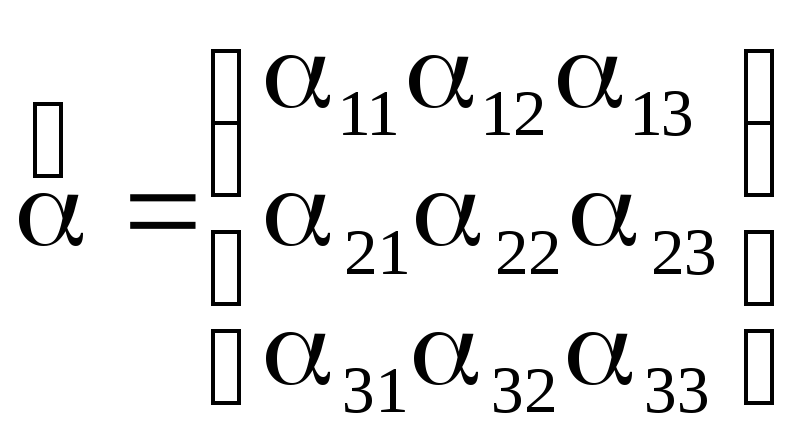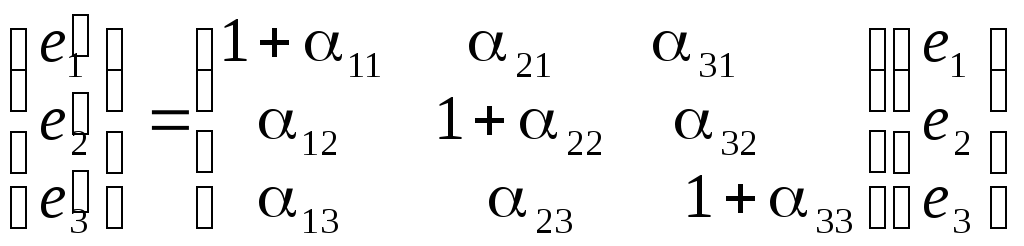
Обозначим матрицу преобразований базиса e к базису e

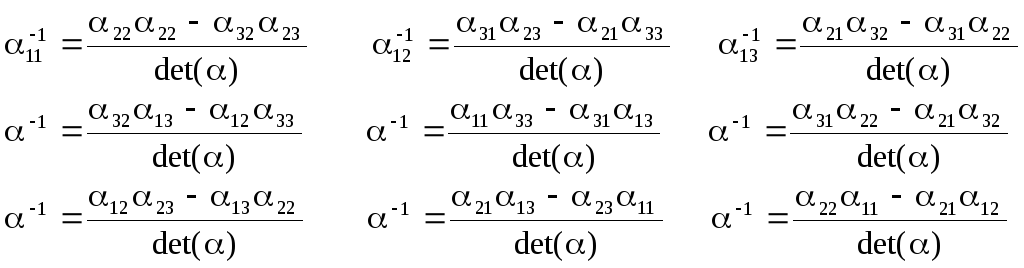
Матрица смещений, как правило, не ортонормированна матрица. Поэтому обратную матрицу нельзя получать транспонированием матрицы.