2013.Термодинамика / Хачатурян01.12.2011

(6.34)

Так как, сумма в общем случае не равна нулю, а суммаесть тождественный нуль в силу условия сохранения числа атомов данного сорта в крис­талле, то уравнение (6.34) можно переписать в виде

(6.35)

Из (6.35) следует искомое соотношение:

(6.36)

Что же касается линейного и кубического членов разложения (6.33), то они отсутствуют в силу симметрии функцииотносительно преобразования инверсии.

Подставляя разложения (6.33) и (6.19) в (6.32), получим:

(6.37)

Выражение типа (6.37) справедливо не только в приближении самосогласованного поля. В общем случае, когда изменение свободной энергии определяется феноменологическим уравнением (6.5), выражение (6.37) можно заменить другим, аналогичным но более общим выражением:

(6.38)

При получении формулы (6.38) из (6.37) мы воспользовались выражениями (6.23) и (6.24), устанавливающими соответствие между феноменологическими коэффициентамиии динамическими константами моделии.

Коэффициентв выражениях (6.33), (6.37), (6.38) представляет собой коэффициент диффузии в идеальном твердом растворе. В этом легко убедиться, положив в (6.37) равными нулю характеристики межатомного взаимодействия — константы. Тогда для декрементаполучим выражение

(6.39) Подставляя теперь (6.39) в формулу (6.31), перепишем последнюю

(6.40)

Функция, имеющая вид, может быть получена также и в результате решения континуального уравнения диффузии

(6.41)

(— оператор Лапласа), в котором использован переход к Фурье–образам функции . коэффициент в уравнении (6.41) играет роль коэффициента диффузии. Именно последнее обстоятельство позволяет сделать вывод о том, что в уравнениях (6.33),коэффициент представляет собой коэффициент диффузии в идеальном твердом растворе.

Рассмотренная выше задача о диффузии атомов по узлам кристаллической решетки имеет, в частности, прямое отношение к задаче о случайных блужданиях в решетке. В самом деле, полагая в (6.31) (это отвечает ситуации, когда в начальный момент времени атом с достоверностью находится в узле) и

(взаимодействие между диффундирующими атомами отсутствует), получим:

(6,42)

Из соотношения (6.14) следует, что амплитудам (6.42) отвечает вероятность, связанная с ними равенством:

, (6.43)

где суммирование и интегрирование производятся по первой зоне Бриллюэна ¹). Выражение для вероятности (6.43) представляет собой решение задачи случайных блужданий. Оно было, по-видимому, впервые получено в работе [39].

При больших значениях параметра— больших временах — главный вклад в интеграл в правой части (6.43) дает область малых значений, так как функцияимеет минимум при

Поэтому мы можем воспользоваться длинноволновой асимптотикой (6.33) для функции . Тогда получим:

. (6.44)

Метод, который был использован при получении асимптотики больших времен (6.44), по существу представляет собой метод перевала. Выражение (6.44) представляет собой решение уравнения диффузии для бесконечной изотропной системы с точечным источником. Это находится в согласии с хорошо известным фактом, что асимптотика больших времен задачи о случайных блужданиях представляет собой решение уравнения диффузии с точечным источником (см., например, [40]).

После этого отступления, касающегося связи между задачей случайных блужданий и линеаризованными уравнениями Онзагера, мы можем вновь обратиться к проблеме спинодального распада.

Выше был выяснен смысл феноменологических коэффициентов в выражении (6.38) для декремента затухания амплитуд концентрационных волн. Температурная зависимость затухания в основ­ном определяется второй производной по концентрации от удельной свободной энергии . Из выражения (6.38) следует, что при температурах, расположенных выше спинодали, когда. декремент затухания есть положительная величина при всех значениях . Обращаясь к выражению (6.31) для временной зависимости амплитуд концентрационных волн, можно видеть, что в условиях, когда, концентрационные неоднородности рассасываются со временем, так как при

При получении формулы (6.43) мы воспользовались правилом перехода от сумирования по волновым векторам квазиконтинуума в первой зоне Бриллюэна к интегрированию по этой зоне:

Ситуация коренным образом изменяется, если температура однородного твердого раствора находится ниже температуры спинодали. В этом случае и декремент затухания, как это следует из (6.38), становится отрицательным для всех значений волновых векторов, расположенных внутри сферы с радиусом, т. е. для. Критическое значение определяется из условия при котором происходит изменение знака декремента затухания (6.38). Напротив, для т. е. , расположенных вне сферы радиуса , декремент затухания всегда является положительной величиной. Из выражения (6.31) следует, что в условиях, когда , концентрационные неоднородности увеличиваются со временем и их амплитуды возрастают по экспоненциальному закону.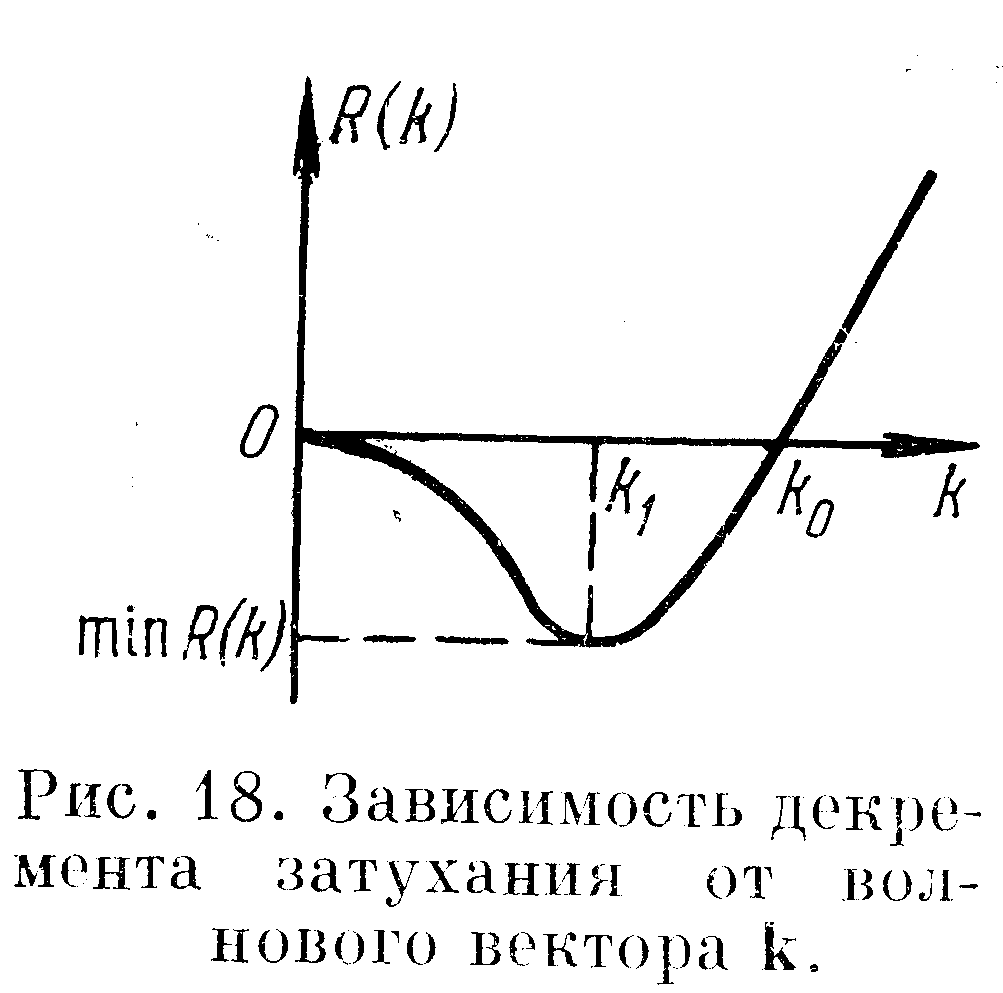

Увеличение амплитудне может происходить неограниченно. Когда принимают достаточно большие значения, выражение (6.5) для, которое было использовано при выводе зависимости (6.38), перестает быть справедливым: в нем необходимо учитывать кубические члены и члены более высокого порядка по концентрационным неоднородностям. Эти члены ограничивают возрастание со временем амплитуд,. Таким образом, выражения (6.31) и (6.38) описывают только начальную стадию спинодального распада, когда увеличивающиеся амплитуды концентрационных волн все еще могут считаться малыми.

Особенности временной эволюции амплитуд концентрационных волн для достаточно интересны, чтобы на них остановиться более подробно. Если построить график зависимости декремента затухания(6.38) как функцию волнового вектора (см. рис. 18), то он обнаруживает минимум для значений удовлетворяющих соотношению

_, (6.45) причем в точке минимума функцияпринимает отрицательное значение, равное

(6.46)

Следовательно (см. (6.31)), в процессе распада быстрее всех растут амплитуды тех волн, волновые векторы которых равны. В изотропных средах эти векторы образуют сферу, имеющую радиус Однако изотропные твердые растворы довольно редко встречаются в природе. Если же принять во внимание упругую анизотропию раствора, то это существенно изменяет все приведенные выше выводы.

Каном было показано [33], что в упруго анизотропных твердых растворах потеря устойчивости осуществляется, в первую очередь, в отношении волн, волновые векторы которых лежат на определенных направлениях симметрии. При этом быстрее всех растут амплитуды, отвечающие волновым векторам, лежащим на направлениях симметрии по обе стороны от структурных узлов обратной решетки на расстоянииот них. Эти волновые векторы образуют звезду, состоящую из нескольких векторов, которую можно обозначить как . В изотропной среде звезда состоит из бесчисленного множества волновых векторов, образующих сферическую оболочку радиуса. Абсолютное значение векторов звезды в анизотропном случае определяется тем же соотношением (6.45), что и в изотропном случае. Разница заключается лишь в том, что для анизотропной среды необходимо учитывать вклад энергии упругих искажений в величину В случае изотропных сред вклад упругой энергии в величину отсутствует.

Результаты, полученные Каном в [32], противоречат последнему выводу. Согласно Кану, величина содержит вклад, обусловленный упругими искажениями, и для изотропной решетки. Этот результат является ошибочным. Не вполне точны и выражения для, полученные Каном для анизотропного случая [33]. Причины неточностей, о которых идет речь, будут подробно рассмотрены в § 40, когда мы вернемся к вопросу о роли энергии упругих искажений при спинодальном распаде. Следует, однако, отметить, что эти неточности не являются существенными: они не влияют на основные качественные выводы, полученные Каном в теории спинодального распада.

Одним из самых интересных и красивых следствий теории спинодального распада является вывод об образовании макропериодических распределений концентрации (модулированных структур) на промежуточных стадиях распада. Для того чтобы убедиться в том, что модулированные структуры действительно могут образовываться в некоторых условиях, рассмотрим кубический упруго–анизотропный раствор, для которого, где упругие постоянные среды. Звезда для такого раствора состоит из шести векторов: ... Векторы звезды направлены вдоль осей [100], [010], [001] соответственно. Абсолютная величина векторов звезды определяется выражением (6.45). Если в выражении (6.6) можно пренебречь амплитудами остальных волн, растущих более медленно, чем волны с волновыми векторами , то распределение концентрации примет вид

_, (6.47) где суммирование производится по всем шести векторам звезды или же

, (6.48) если для всех значений некоторая фаза. Величиныкоординаты радиуса-вектора в ортогональной системе координат, связанной соответственно с осями . Выражение (6.48) описывает трехмерное пространственное периодическое распределение концентрации. Приведенные соображения были использованы Каном [33] для объяснения существования макропериодических распределений состава (модулированных структур), появляющихся во многих сплавах на ранних стадиях распада.

Широкая распространенность и своеобразие этого явления, занимающего особое место среди явлений, возникающих при фазовых превращениях, делает актуальными поиски его теоретического объяснения. Несмотря на всю привлекательность только что изложенного простого объяснения механизма образования модулированных структур, оно, по-видимому, не может считаться универсальным и пригодным во всех случаях. Дело в том, что при получении периодического распределения (6.48) было сделано одно весьма серьезное допущение: было принято, что в процессе спинодального распада можно пренебречь амплитудами всех волн, кроме волн, которые растут с максимальной скоростью. Если предположить, что амплитуды всех концентрационных волн, относительно которых потеряна устойчивость однородного раствора, могут неограниченно возрастать со временем по закону (6.31), то сделанное допущение оказывается справедливым, и мы действительно приходим к распределению концентраций, имеющему вид (6.48).

Для того чтобы убедиться в этом, необходимо в выражении для фурье–оригинала функции перейти к асимптотике больших времен, используя для этой цели метод перевала. Соответствующая программа вычислений выполнена в Приложении 1.

Существует, однако, опасность, что еще до того, как выражение дляначинает описываться асимптотикой типа (6.48), сами неоднородности перестают быть малыми. В этом случае мы уже не можем ограничиться линейной аппроксимацией (6.27) кинетических уравнений (6.25): в последних становятся существенными нелинейные члены, которые и будут определять асимптотику больших времен. Асимптотика больших времен для решения нелинейных уравнений будет существенно отличаться от той, которая была получена из решения (6.31) линеаризованного кинетического уравнения. Таким образом, предположение, согласно которому в выражении дляможно сохранить лишь волны, принадлежащие звезде, оказывается несправедливым, и модулированная структура, описываемая выражением (6.48), не может возникнуть.

Из всего вышесказанного следует, что модулированные структуры, описываемые выражением (6.48), могут возникать в особых условиях, на промежуточных стадиях спинодального распада, когда асимптотика больших времен достигается при малых значениях неоднородностей . Модулированные структуры, образовавшиеся таким образом, обязаны своим происхождением чисто кинетическим эффектам.

При обсуждении кинетики спинодального распада подразумевалось, что уравнения (6.25) описывают распад однородного твердого раствора вплоть до достижения им равновесного состояния. Последнее обстоятельство, однако, не представляется таким очевидным. Можно всегда представить себе альтернативный случай, когда в результате распада образуется не равновесное, а промежуточное метастабильное состояние. Если при описании эволюции системы оставаться в рамках приближения кинетических уравнений (6.25) (приближение уравнения диффузии), то при достижении метастабильного состояния дальнейшая эволюция системы прекращается (так как в метастабильном (6.25) скорость процесса ).

Как мы уже знаем, метастабильное состояние является относительно устойчивым, и система может выйти из него только флюктуацион-ным путем, преодолев при этом энергетический барьер конечных размеров. Кинетика, осуществляемая в результате флюктуационного преодоления барьеров, имеет качественно иную физическую природу и не описывается уравнениями (6.25). Она требует для своего описания другого математического аппарата.

Таким образом, мы неожиданно сталкиваемся с ситуацией, когда метастабильные состояния, возникающие в процессе рас­пада твердого раствора, выступают в новой и важной роли, в зна­чительной степени определяющей как особенности протекания кинетики распада, так и промежуточные устойчивые состояния, характеризующиеся, в общем случае, неоднородным распределением концентрации.

Вопрос о таких метастабильных состояниях чрезвычайно интересен и заслуживает специального обсуждения. Оно будет проведено в § 8 настоящей главы. Там же будет показано, что распределение концентраций в метастабильных состояниях твердого раствора может иметь прямое отношение к модулированным структурам, наблюдаемым при распаде,