2013.Термодинамика / Диаграммы состояния

Диаграммы состояния бинарных систем

Мы рассмотрим некоторые особые случаи когда из диашрам состояния мложно получить термодинамические данные.

Теперь мы рассмотрим равновесие фаз с более общей точки зрения. В этом случае мы не получим количественных данных, но получим качественные выводы.

Исследуем общую форму кривой свободной энергии – состав.

Свободная энергия смешения при каком-либо данном составе будет выражаться уравнением

Дифференцируем по X_B

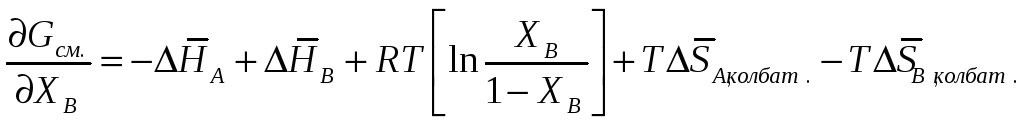
Мы рассмотрим очень разбавленный раствор компонентов B в A. Поэтому можно положить, что и равны нулю. .

Таким образом,

В очень разбавленном растворе и не зависят от состава в области разбавленного раствора (Каждый атом В изолирован и помещен в чистый компонент).

Значение зависит от состава только через и при достаточно малом значении отрицательной величиной независимо от знака и .

Таким образом, растворение в кристалле вещества всегда приводит к уменьшению свободной энергии Гиббса. Следовательно, чистая фаза всегда термодинамически неустойчива.

Этот вывод важен для процесса изготовления сверхчистых материалов. Из него следует, что чистый материал всегда будет стремиться к загрязнению за счет поглощения примесей из окружающей среды. Если чистый материал в тигле , то материал тигля имеет тенденцию растворяться в материале.

Зависимость свободная энергия состав, когда компоненты А и В имеют одинаковую кристаллическую структуру.

В этом случае теоретически возможно образование непрерывного ряда твердых растворов. Если А и В имеют различные кристаллические структуры непрерывный ряд твердых растворов невозможен.

Известно, что при данной температуре. Но если , , как функция X_B, отрицательна при всех составах. . Но если , положение осложняется. Форма кривой свободная энергия – состав может сильно изменяться с температурой. При высоких температурах вклад будет иметь большее значение, чем при низких температурах.

При очень высоких температурах кривая будет вогнутой при всех составах.

Однако, при низких температурах начнет преобладать в выражении для , и кривая будет иметь тенденцию стать положительной. В близи концов бинарной системы свободная энергия отрицательна. При X_B=0 и 1 Так ч то по кривая будет иметь вид.

Если раствор регулярный, то минимумы симметричны относительно X_B=0,5. Для составов а и с раствор более устойчив относительно чистых компонентов. Необходимо рассмотреть еще возможность распада на два однородных твердых раствора.

П редположим, что раствор с концентрацией x распадается на два раствора c концентрацией d и e. Свободная энергия этой механической смеси растворов будет равна сумме свободных энергий этих растворов. Свободная энергия раствора состава d равна , а свободная энергия раствора состава e равна

Положение точки B ниже точки А (исходного значения энергии однородного раствора состава x). - можно еще понизить за счет обогащение раствора e компонентом B и раствора состава d компонентом А. Этот процесс можно продолжать до точек Y и F , которые имеют общую касательную к кривой .

При концентрации растворов y и f компоненты будут иметь в растворах одинаковые химические потенциалы и дальнейшее снижение свободной энергии Гиббса за счет распада станет невозможным. Следует отметить, что растворы состава y,f не обязательно совпадают с минимумами кривой .Свободные энергии E,F могут значительно отличаться от минимальных значений. Поскольку критерием равновесия фаз является равенство химических потенциалов, а не минимальные значения свободных энергий отдельных фаз.

Однородные растворы слева и справа от точек y,z устойчивы, а между этими точками не устойчивы относительно распада на два раствора.

Рассмотренная кривая свободной энергии связана с пределом несмешиваемости на диаграмме состояния. При более высоких температурах минимумы сближаются по составу и полностью исчезают при критической температуре T_кр.. Тип диаграммы состояния относящийся к рассмотренной на рисунке зависимости . имеет вид.

М ежду точками y и z существуют две точки перегиба. Их также наносят на диаграмму состояния. Полученная таким способом кривая называется спинодалью. Она играет важную роль в кинетике распада фаз.

Рассмотрим активность компонентов A и B, характерную для данного типа кривой .

Возьмем в качестве примера компонент B. Находим разность химических потенциалов для любого состава. Для этого для заданного состава X_B проводим касательную к кривой до пересечения ее с линией X_B=1. Длина отрезка [0,точка пересечения] равна разности химических потенциалов. Значение активности a_B получаем из выражения

При составе y и z компонент B будет иметь одинаковую активность в соответствии с требованиями равновесия . Максимумы и минимумы a_B соответствуют спинодальным точкам зависимости . Площади заштрихованных двух частей должна быть равны (рис.4).