
- •A) Определение концентрации микроорганизмов в счетной камере.
- •Б) Определение концентрации живых микроорганизмов путем высева на плотные питательные среды
- •В) раздел пропущен за ненадобностью
- •2. Определение концентрации бактерий, фагов, вирусов и риккетсий по результатам посева крайних разведений исследуемой культуры на жидкие питательные среды
- •Действие различных доз культуры вируса западного энцефаломиелита лошадей на культуру тканей куриного эмбриона
- •Коэффициенты для расчета границ доверительных интервалов концентраций, вычисленных по формуле (34)
Ашмарин И.П., Воробьев А.А. Статистические методы в микробиологических исследованиях. - Л.: Государственное издательство медицинской литературы, 1962. - 182 с.
Глава
СТАТИСТИЧЕСКАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ ОПРЕДЕЛЕНИЯ КОНЦЕНТРАЦИИ И БИОЛОГИЧЕСКОЙ АКТИВНОСТИ МИКРООРГАНИЗМОВ И ТОКСИНОВ
1. ОПРЕДЕЛЕНИЕ КОНЦЕНТРАЦИИ МИКРООРГАНИЗМОВ ПУТЕМ НЕПОСРЕДСТВЕННОГО ПОДСЧЕТА ПОД МИКРОСКОПОМ ИЛИ ПО ЧИСЛУ КОЛОНИЙ, ОБРАЗУЮЩИХСЯ ПРИ ВЫСЕВАХ НА ПЛОТНЫЕ ПИТАТЕЛЬНЫЕ СРЕДЫ
Методы определения концентрации микроорганизмов, рассматриваемые в настоящем параграфе, требуют приемов статистической обработки, несколько отличающихся от изложенных ранее (традиционных, прим. К.Е.В.). Причиной этого является своеобразие законов, которым подчиняется варьирование такого рода данных (сноска: закон Пуассона (34, 40)). Не рассматривая здесь существо этих законов, обратимся сразу к одному из его следствий. Оно сводится к тому, что квадратичное отклонение непосредственно подсчитанного числа микроорганизмов или их колоний равно корню квадратному из этого же числа. Иначе говоря, квадратичное отклонение в такого рода опытах можно вычислить по формуле:
 (26)
(26)
где
 - число непосредственно подсчитанных
микроорганизмов или колоний. Следует
подчеркнуть, что
- число непосредственно подсчитанных
микроорганизмов или колоний. Следует
подчеркнуть, что
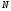 - это именно непосредственно
находимое
в опыте число. Так, например, если на
поверхности агара в чашке Петри мы
насчитали 25 колоний, то квадратичное
отклонение следует рассчитывать, исходя
из этого числа, а не из числа, получаемого
при последующем вычислении концентрации
микроорганизмов в исходной культуре.
Формула (26) дает удовлетворительные
результаты при условии, что
- это именно непосредственно
находимое
в опыте число. Так, например, если на
поверхности агара в чашке Петри мы
насчитали 25 колоний, то квадратичное
отклонение следует рассчитывать, исходя
из этого числа, а не из числа, получаемого
при последующем вычислении концентрации
микроорганизмов в исходной культуре.
Формула (26) дает удовлетворительные
результаты при условии, что
 превышает 15. Кроме того, следует помнить,
что она не применима в тех случаях, когда
не исключено влияние ряда причин,
отражающихся на точности результатов
опыта. Такими причинами могут быть:
1) неточность приготовления разведений
исходной культуры, 2) наличие в микробной
суспензии существенного количества
конгломератов, включающих более чем
одну жизнеспособную микробную клетку,
которые при последующем высеве на
плотную питательную среду образуют
единичные колонии и 3) колебания в составе
питательной среды или особая лабильность
исследуемого микроорганизма, которые
могут привести к тому, что в отдельных
случаях существенная доля высеянных
живых микроорганизмов не образует
колоний (последнее может иметь место,
например, в случае заражения вирусами
тех или иных органов или тканей животных
с последующей регистрацией участков
повреждения или размножения вирусов).
Если не исключена возможность отклонений
по перечисленным выше причинам, то
статистическую обработку результатов
следует вести только с помощью общих
методов, изложенных в гл. 1.
превышает 15. Кроме того, следует помнить,
что она не применима в тех случаях, когда
не исключено влияние ряда причин,
отражающихся на точности результатов
опыта. Такими причинами могут быть:
1) неточность приготовления разведений
исходной культуры, 2) наличие в микробной
суспензии существенного количества
конгломератов, включающих более чем
одну жизнеспособную микробную клетку,
которые при последующем высеве на
плотную питательную среду образуют
единичные колонии и 3) колебания в составе
питательной среды или особая лабильность
исследуемого микроорганизма, которые
могут привести к тому, что в отдельных
случаях существенная доля высеянных
живых микроорганизмов не образует
колоний (последнее может иметь место,
например, в случае заражения вирусами
тех или иных органов или тканей животных
с последующей регистрацией участков
повреждения или размножения вирусов).
Если не исключена возможность отклонений
по перечисленным выше причинам, то
статистическую обработку результатов
следует вести только с помощью общих
методов, изложенных в гл. 1.
Заметим,
что под
 в формуле (26) подразумевается результат
единичного определения, т. е. например,
результат подсчета микроорганизмов в
одном препарате или подсчете колоний
в одной чашке Петри. Если же необходимо
в формуле (26) подразумевается результат
единичного определения, т. е. например,
результат подсчета микроорганизмов в
одном препарате или подсчете колоний
в одной чашке Петри. Если же необходимо
 оценить
доверительный интервал средней из ряда
параллельных определений, то следует
воспользоваться формулой:
оценить
доверительный интервал средней из ряда
параллельных определений, то следует
воспользоваться формулой:

 (27a)
(27a)
для уровня достоверности 95 %; или формулой
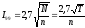 (27б)
(27б)
для уровня достоверности 99 %, где - число определений, Т - общее число
микроорганизмов
или колоний, найденных во всех изученных
препаратах, а
 или
или
 - среднее число микроорганизмов или
колоний
- среднее число микроорганизмов или
колоний
 .
При этом предполагается, что все препараты
приготовлены из одного и того же
разведения одной культуры.
.
При этом предполагается, что все препараты
приготовлены из одного и того же
разведения одной культуры.
Если нас интересует доверительный интервал средней не в абсолютном, а в относительном выражении, например, в процентах к величине средней, то можно воспользоваться формулами:
 % (28а)
% (28а)
для уровня достоверности 95 % и
 (28б)
(28б)
для уровня достоверности 99 %
Обратимся теперь к детальному описанию статистической обработки данных, получаемых с помощью отдельных, наиболее распространенных, методов определения концентрации микроорганизмов.
A) Определение концентрации микроорганизмов в счетной камере.
Как
известно, в счетную камеру помещается
разведенная суспензия окрашенных
микроорганизмов, после чего под
микроскопом подсчитывается число
клеток, наблюдаемых в пределах ряда
квадратов сетки, наносимой на поверхность
камере. Каждый малый квадрат сетки
соответствует определенному объему -
v - микроскопируемой суспензии (обычно
1/4000000 мл). Если в просмотренных n малых
квадратах найдено всего T микроорганизмов,
то среднее число микроорганизмов,
соответствующее одному малому квадрату,
равно
 .
.
Отсюда
концентрация микроорганизмов в данной
суспензии составляет
 .
Если при подготовке суспензии для
микроскопии в камере исходная культура
была разведена в k раз, то концентрация
в культуре выразится формулой:
.
Если при подготовке суспензии для
микроскопии в камере исходная культура
была разведена в k раз, то концентрация
в культуре выразится формулой:
 (29a)
(29a)
Напомнив,
таким образом, последовательность
расчетов, связанных с применением
счетных камер, обратимся к конкретному
примеру. Допустим, в камере Горяева при
просмотре разведенной в 100 раз культуры
E. coli найдено в 20 малых квадратах всего
144 клетки. Отсюда среднее количество
клеток в одном квадрате
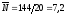 .
По формуле (27а)
находим доверительный интервал для
.
По формуле (27а)
находим доверительный интервал для
 с
уровнем достоверности 95 %:
с
уровнем достоверности 95 %:

или в относительном выражении - по формуле (28а):
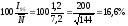
В камере Горяева одному малому квадрату соответствует объем 1/4000000 мл. Следовательно, по формуле (29а) концентрация в исходной культуре составляет:
 клеток/мл
клеток/мл
Доверительный
интервал найденной концентрации в
относительном выражении будет тем же,
что был найден для
 ,
т.е. 16,6% . В абсолютном выражении он
составит, очевидно, 2,881090,48109
клеток/мл. Таким образом, с вероятностью
95% можно полагать, что действительная
концентрация клеток E. coli в исходной
культуре находится в интервале от
2,40109
до 3,36109
клеток/мл.
,
т.е. 16,6% . В абсолютном выражении он
составит, очевидно, 2,881090,48109
клеток/мл. Таким образом, с вероятностью
95% можно полагать, что действительная
концентрация клеток E. coli в исходной
культуре находится в интервале от
2,40109
до 3,36109
клеток/мл.
Если нужно оценить доверительный интервал с вероятностью 99% , то производим аналогичный расчет с помощью формул (27б) и (28б). Легко показать, что в том же примере результат составит 2,881090,65109 клеток/мл.
Рассмотрим
теперь встречающийся иногда в практике
случай, когда концентрация микроорганизмов
оценивается по результатам микроскопирования
в камерах двух или более различных
разведений одной и той же культуры. В
этом случае при расчете концентрации
в исходной культуре следует исходить
из среднего взвешенного количества
микроорганизмов
 на один малый квадрат счетной камеры,
которое вычисляется из частных средних,
найденных для каждого из просмотренных
разведений культуры (с поправкой на
разную степень разведения), по формуле:
на один малый квадрат счетной камеры,
которое вычисляется из частных средних,
найденных для каждого из просмотренных
разведений культуры (с поправкой на
разную степень разведения), по формуле:
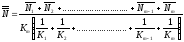 (30)
(30)
где
 ,
,
 ,………….
,…………. ,
,
 - средние количества микроорганизмов
в одном малом квадрате, найденные при
просмотре в камере 1-го, 2-го (m-1)-го и m-го
разведений культуры, пронумерованных
в порядке возрастания кратности
разведения суспензии, а К1,
К2,………..Кm-1,
Кm,
- величины соответствующих кратностей
разведения суспензии. При конечном
расчете концентрации в исходной культуре
формула (29а)
в данном случае примет вид:
- средние количества микроорганизмов
в одном малом квадрате, найденные при
просмотре в камере 1-го, 2-го (m-1)-го и m-го
разведений культуры, пронумерованных
в порядке возрастания кратности
разведения суспензии, а К1,
К2,………..Кm-1,
Кm,
- величины соответствующих кратностей
разведения суспензии. При конечном
расчете концентрации в исходной культуре
формула (29а)
в данном случае примет вид:
 (29б)
(29б)
Расчет
доверительного интервала для
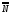 также видоизменяется. В относительном
выражении доверительный интервал как
также видоизменяется. В относительном
выражении доверительный интервал как
 ,
так и концентрации в исходной культуре
вычисляется по формуле:
,
так и концентрации в исходной культуре
вычисляется по формуле:
 (31a)
(31a)
для уровня достоверности 95% и

для
уровня достоверности 99%. Здесь
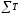 обозначает сумму общих количеств клеток,
подсчитанных во всех просмотренных
квадратах каждой из камер.
обозначает сумму общих количеств клеток,
подсчитанных во всех просмотренных
квадратах каждой из камер.
Приведем
пример. Допустим, что определение
концентрации микробных клеток
производилось в двух камерах Горяева
(v=1:4000000). В первую помещена культура E.
coli, разведенная в 20 раз (K1)
, а во вторую - та же культура, разведенная
в 100 раз (K2).
В первой при просмотре 20 малых квадратов
найдено 256, а во второй в 27 квадратах
найдена 81 клетка. Отсюда
 ,
а
,
а
 Далее
Далее
 =2,63
=2,63
Следовательно, концентрация в исходной культуре составит по формуле(29б):
 клеток/мл
клеток/мл
Доверительный
же интервал как
 ,
так и концентрации культуры в относительном
выражении составит по формуле (31а):
,
так и концентрации культуры в относительном
выражении составит по формуле (31а):
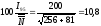 %
%
для уровня вероятности 95 %, а по формуле (31б):
 %
%
для уровня вероятности 99 %. Таким образом, действительное значение концентрации клеток в исходной культуре с вероятностью 95 % находится в интервале 1,05109 0,11109, а с вероятностью 99 % - 1,05109 0,15109.
Посмотрим теперь, как убедиться в существенности различий концентраций в двух культурах, если определения проводились с помощью счетных камер. Для этого наиболее удобны критерии, выражаемые неравенствами:
 (32a)
(32a)
уровень вероятности 95 % и
 (32б)
(32б)
уровень вероятности 99 %,
где
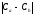 - абсолютная величина разности концентраций
микроорганизмов в сравниваемых культурах,
а
- абсолютная величина разности концентраций
микроорганизмов в сравниваемых культурах,
а
 и
и
 - общие количества микроорганизмов,
подсчитанных в камере при определении
соответствующей культуры.
- общие количества микроорганизмов,
подсчитанных в камере при определении
соответствующей культуры.
Так,
например, при сравнении двух культур
СТИ с помощью подсчета в камерах
установлены концентрации 254106
и
477106
клеток/мл.
При определении концентрации в первой
культуре общее число микроорганизмов,
подсчитанных в камере, составило 124, а
при определении во второй культуре -
145. Подставим эти значения в формулу
(32а).
Левая часть неравенства составит
 ,
правая часть -
,
правая часть -
 .
Поскольку 223>90, можно с вероятностью
95 % считать, что наблюдаемое различие
концентраций достоверно. Воспользовавшись
формулой (32б),
можно также показать, что в приведенном
примере различие концентраций достоверно
и с вероятностью 99 %.
.
Поскольку 223>90, можно с вероятностью
95 % считать, что наблюдаемое различие
концентраций достоверно. Воспользовавшись
формулой (32б),
можно также показать, что в приведенном
примере различие концентраций достоверно
и с вероятностью 99 %.
В заключение остановимся на оценке доверительного интервала отношения концентраций двух культур. Это можно сделать с помощью формул:
 , (33а)
, (33а)
уровень вероятности 95 %
 , (33б)
, (33б)
уровень вероятности 99 %.
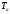 и
и
 имеют здесь то же значение, что и в
формулах (31а)
и (32б).
Обращаясь вновь к только что использованному
примеру, находим, что отношение
концентраций сравниваемых культур СТИ
составляет:
имеют здесь то же значение, что и в
формулах (31а)
и (32б).
Обращаясь вновь к только что использованному
примеру, находим, что отношение
концентраций сравниваемых культур СТИ
составляет:
 .
.
Далее по формуле (33а):
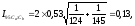
а по формуле (33б):

Таким образом, с вероятностью 95 % можно полагать, что истинное значение отношения концентраций расположено в интервале 0,53±0,13, а с вероятностью 99 % - в интервале 0,53±0,18.
