DisMathTPU

51

Методы поиска минимальной и кратчайшей ДНФ будут рассмотрены далее, пока же найдем их визуально по матрице Грея.

Примеры. Для функции f(x; y; z) из предыдущего примера сокращенная ДНФ является и кратчайшей, и минимальной:

МинДНФf = КратДНФf = z _ x y (длины 2, ранга 3).

Однако эта функция имеет еще одну кратчайшую ДНФ:

z y

КратДНФ0f = z _ x y z (длины 2, ранга 4).

x

КратДНФ0

f отличается от КратДНФf тем, что ее вторая конъюнкция не является простой импликантой, ее можно упростить вычеркиванием z.

Теорема о кратчайшей ДНФ. Существует кратчайшая ДНФ булевой функции, состоящая из простых импликант.

Доказательство (конструктивное). Рассмотрим произвольную булеву функцию f(x1; : : : ; xn). Докажем сначала вспомогательный результат. Пусть функция g(x1; : : : ; xn) импликанта функции f(x1; : : : ; xn), тогда

g(x1; : : : ; xn) _ f(x1; : : : ; xn) = f(x1; : : : ; xn):

Åñëè g(x1; : : : ; xn) = 0, то обе части этого выражения равны f(x1; : : : ; xn). Åñëè g(x1; : : : ; xn) = 1, òî è f(x1; : : : ; xn) = 1 (òàê êàê g(x1; : : : ; xn) импликанта функции f(x1; : : : ; xn)), а значит, обе части равны 1. Рассмотрим теперь КратДНФf функции f(x1; : : : ; xn).

КратДНФf = K1 _ K2 _ : : : _ Kl:

Если все ее конъюнкции являются простыми импликантами функции, то кратчайшая ДНФ, состоящая из простых импликант, найдена. Иначе пусть K1 не простая импликанта функции f(x1; : : : ; xn), тогда существует про-

такая, что K1 _ K10 = K10 . По доказанному верно

КратДНФf = K10 _ КратДНФf = K10 _ K1 _ K2 _ : : : _ Kl = = K10 _ K2 _ : : : _ Kl = КратДНФ0f :

Длина КратДНФ0

f равна длине КратДНФf . Повторив те же рассуждения для всех остальных конъюнкций КратДНФ 0

f , мы получим кратчайшую ДНФ функции f(x1; : : : ; xn), состоящую из простых импликант.

53

Примеры. Найдем сокращенную, кратчайшие и минимальные ДНФ функции f(a; b; c; d):

На левой матрице показано множество всех максимальных интервалов (их номера можно найти на двух других матрицах).

СокрДНФf = a b c _ a b d _ a b c _ a b d _ a c d _ a b d _ a b c _ c d. K1 K2 K3 K4 K5 K6 K7 K8

В центре показано достаточное множество из пяти максимальных интервалов fI1; I2; I3; I4; I5g. Никакие четыре из восьми максимальных интервалов не образуют достаточного множества, следовательно, ДНФ, состоящая из конъюнкций, заданных интервалами I1 I5, является кратчайшей (дли- ны 5, ранга 15):

КратДНФf = a b c _ a b d _ a b c _ a b d _ a c d.

Справа показано достаточное множество из пяти максимальных интервалов fI1; I2; I6; I7; I8g. Никакое другое достаточное множество не дает мень-

шей суммы рангов, следовательно, соответствующая ДНФ является минимальной (длины 5, ранга 14):

МинДНФf = a b c _ a b d _ a b d _ a b c _ c d. K1 K2 K6 K7 K8

Обратим внимание, что в данном случае КратДНФ f не является мини-

мальной, а МинДНФf является кратчайшей. Других кратчайших и мини-

мальных ДНФ эта функция не имеет (напомним, что мы рассматриваем только простые кратчайшие ДНФ).

9.3. Безызбыточная ДНФ

Определение. ДНФ булевой функции f(x1; : : : ; xn) называется безыз-

быточной ДНФ (БезДНФf ), если из нее нельзя удалить ни одной конъ-

юнкции и ни одной переменной из конъюнкции так, чтобы она оставалась равносильной исходной ДНФ.

54

В частности, безызбыточной является любая минимальная и любая крат- чайшая ДНФ (не простая кратчайшая ДНФ явно избыточна).

Методы поиска безызбыточных ДНФ будут рассмотрены далее. Здесь же мы найдем безызбыточную ДНФ по матрице Грея. Для этого выделим такое достаточное множество максимальных интервалов, чтобы при удалении любого интервала оно переставало быть достаточным.

Примеры. Рассмотрим функцию из предыдущего примера.

Слева выделено достаточное множество из пяти интервалов, ни один из

которых нельзя удалить так, чтобы множество оставалось достаточным. Но интервал I0 не максимальный, так как он может быть расширен по

первой компоненте, то есть из конъюнкции K0 = a c d можно удалить пе-

ременную a. Поэтому ДНФ, состоящая из конъюнкций, заданных этими интервалами, не является безызбыточной, но если упростить K0, òî ÄÍÔ

станет безызбыточной и совпадет с МинДНФ из предыдущего примера.

В центре выделено достаточное множество из шести максимальных интервалов, которое является избыточным, так как интервал I00 может быть

удален, а множество при этом останется достаточным. Поэтому ДНФ, со-

стоящая из конъюнкций, заданных шестью выделенными интервалами, не является безызбыточной, но если удалить интервал I00, то ДНФ станет

безызбыточной и совпадет с кратчайшей ДНФ из предыдущего примера. Справа выделено достаточное множество If из шести максимальных ин-

тервалов (с номерами из предыдущего примера). Удаление любого из них приводит к тому, что множество перестает быть достаточным. Поэтому множество If задает безызбыточную ДНФ (длины 6, ранга 17):

БезДНФf = a b c _ a b d _ a b d _ a c d _ a b d _ c d. K1 K2 K4 K5 K6 K8

Сравнение длин и рангов ДНФ из двух последних примеров, показывает, что эта безызбыточная ДНФ не является ни кратчайшей, ни минимальной.

Обратим внимание, что все конъюнкции, задаваемые ядерными интервалами (в нашем примере это интервалы I1 è I2), входят во все безызбы- точные ДНФ, в том числе во все кратчайшие и минимальные ДНФ.

56

В разделе 8.5 для этой же функции разложением Шеннона была полу- чена другая ДНФf = x _ x z. В результате имеем

Убедимся в том, что они равносильны, построив матрицы Грея:

I3 I5

9.5. Упражнения

Упр.1. Определить, являются ли конъюнкции K1 K3 импликантами булевых функций f1 f3 непосредственно по определению импликанты.

Упр.2. Из заданных множеств элементарных конъюнкций выделить простые импликанты функций f1 f3, представив их матрицами Грея:

fac; a b; a c; ag; f1(a; b; c) = 00101111;

fa b; b c; ag; f2(a; b; c) = 01111110;

fb d; b c; a b cg; f3(a; b; c; d) = 1010111001011110:

Найти все простые импликанты функций f1 f3.

Упр.3. Найти сокращенную ДНФ, все кратчайшие ДНФ и все безызбыточные ДНФ следующих булевых функций:

Упр.4. Найти ДНФ булевых функций, заданных формулами F1 F6,

подстановкой кратчайших ДНФ элементарных булевых функций. Проверить правильность вычислений построением таблиц истинности или сравнением с результатами из упр. 6 подраздела 8.6.

F1 = x ! y z ! x y; F2 = x y - (x z);

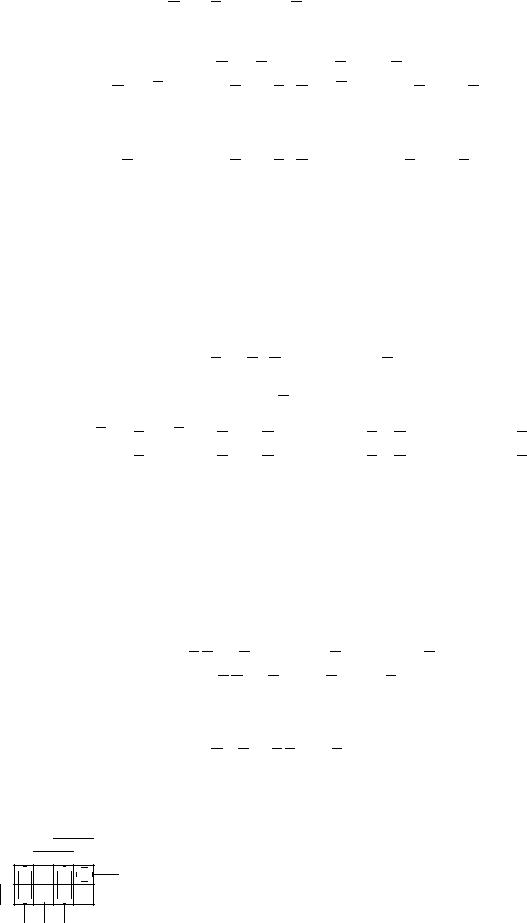
59

3) Получим ДНФ0 по формуле (F ) разложением по переменным. Применим к подформуле (x ! yz)=(y z) разложение Шеннона по переменной y (эта переменная встречается чаще x и так же часто, как z).

(F ) = ((x ! yz)=(y z)) _ xyz =

= y[(x ! 1z)=(1 z)] _ y[(x ! 0z)=(0 z)] _ xyz =

[применим свойства 0 и 1 для конъюнкции ]

=y[(x ! 0)=(1 z)] _ y[(x ! z)=(0 z)] _ xyz =

[ выведем свойства 0 и 1 для импликации и эквивалентности

èупростим выражение ]

=y[x=z] _ y[(x ! z)=z] _ xyz =

[разложим коэффициенты при y è y по переменной z ]

=y [z (x=1) _ z (x=0)] _ y [z ((x ! 1)=1) _ z ((x ! 0)=0)] _ x y z =

=y [z (x=0) _ z (x=1)] _ y [z ((x ! 1)=1) _ z ((x ! 0)=0)] _ x y z =

[ выведем свойства 0 и 1 для импликации и штриха Шеффера

èупростим выражение ]

=y [z1 _ z x] _ y [z(1=1) _ z(x=0)] _ x y z =

=y [z _ z x] _ y [z0 _ z1] _ x y z =

[ используем свойства 0 и 1 и закон дистрибутивности ]

= y z _ x y z _ y z _ x y z = ÄÍÔ0: K1 K2 K3 K4

4) Построим матрицу Грея по ДНФ 0.

60

5) Получим ДНФ00 по формуле (F ) подстановкой кратчайших ДНФ элементарных функций. Заменим штрих Шеффера a=b кратчайшей ДНФ при a = x ! yz, b = y z:

b a=b = a _ b a

(F ) = ((x ! yz)=(y z)) _ xyz = ((x ! yz) _ (y z)) _ xyz =

[ заменим инверсию импликации на не импликацию и инверсию эквивалентности на дизъюнкцию с исключением ]

= (x ,! yz) _ (y z) _ xyz =

[ найдем кратчайшие ДНФ не импликации и дизъюнкции с исключением

èподставим их в формулу ]

=x (y z) _ (y z _ y z) _ x y z =

[ применим законы де Моргана, дистрибутивности и ассоциативности ]

=x (y _ z) _ y z _ y z _ x y z =

=x y _ x z _ y z _ y z _ x y z = ÄÍÔ00:

K1 K2 K3 K4 K5

40) Построим матрицу Грея по ДНФ 00.

z y I

- 2 I

- 1

x? ? ?

I4 I5 I3

6) Построим сокращенную ДНФ по матрице Грея . Выделим все максимальные интервалы, они зададут конъюнкции сокращенной ДНФ.

x? ? ?

I1 I2 I3