
DisMathTPU
.pdf
41
f3(x; y; z) = x y z ! (x z _ (x y)) ïî fxg; fx; y; zg,
f4(x; y; z; t) = y z x t=(x ! z t) (x _ y _ z) ïî fx; yg; fz; tg. Показать равносильность формул, полученных двумя способами.
Упр.2. Построить совершенные ДНФ и совершенные КНФ булевых функций f1 f8.
x y z |
f1 |
f2 |
f3 |
f4 |
f5 |
f6 |
f7 |
f8 |
||
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
8. Дизъюнктивная нормальная форма
8.1. Элементарная конъюнкция и ДНФ
Пусть имеем множество переменных X = fx1; x2; : : : ; xng.
Определение. Элементарной конъюнкцией назовем конъюнкцию переменных множества X, в которую каждая переменная входит не более
одного раза (с инверсией или без инверсии).
Примеры. Пусть X = fx1; x2; x3; x4g, тогда x1x2x4, x1x3, x1, 1 являются элементарными конъюнкциями, а x1x1x2, x1x2x2x4 не являются.
Определение. Число переменных, образующих элементарную конъюнкцию, назовем ее рангом.
Примеры. Ранги элементарных конъюнкций x1x3x4 и 1 равны трем и íóëþ.
Определение. Полной конъюнкцией назовем элементарную конъюнкцию, состоящую из всех n переменных множества X, то есть конъюнкцию
ранга n.
Пример. При n = 4 конъюнкция x1x2x3x4 полная. Определение. Две конъюнкции называются ортогональными по пере-
менной xi, если эта переменная входит в одну конъюнкцию с инверсией, а в другую без инверсии.
Пример. Конъюнкции x1x2x3 è x1x3x4 ортогональны по переменным x1 è x3.
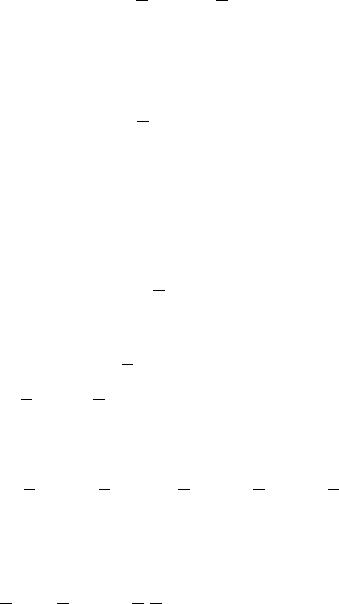
42
Определение. Две конъюнкции называются смежными, если они ортогональны по одной и только одной переменной xi (принято также гово- рить смежны по переменной xi ).
Пример. Конъюнкции x1x2x3 è x1x3x4 менной x3 (ортогональны только по x3).
Определение. Две конъюнкции называются соседними, если они ортогональны по одной и только одной переменной xi и совпадают по остальным (принято также говорить соседние по переменной xi ).
Пример. Конъюнкции x1x2x3 è x1x2x3 являются соседними по переменной x3 (ортогональны только по x3 и совпадают по x1 è x2).
Законы склеивания и обобщенного склеивания применяются, как нетрудно видеть, к соседним и смежным конъюнкциям соответственно. Поэтому их также называют законами склеивания соседних конъюнкций и обобщенного склеивания смежных конъюкнций и иногда добавляют, по какой именно переменной.
Примеры. Конъюнкции x1x2x3 è x1x2x3 являются соседними по пе- ременной x3, следовательно, к ним применим закон склеивания соседних конъюнкций по x3:
x1x2x3 _ x1x2x3 = x1x2:
Конъюнкции x1x2x3 è x1x3x4 являются смежными по переменной x3, следо- вательно, к ним применим закон обобщенного склеивания смежных конъюнкций по x3:
x1x2x3 _ x1x3x4 = x1x2x3 _ x1x3x4 _ x1x2x4:
Определение. Дизъюнктивной нормальной формой (ДНФ) булевой функции f(x1; : : : ; xn) назовем дизъюнкцию различных элементарных конъюнкций, задающую функцию f(x1; : : : ; xn).
Пример. x1x2 _ x1x2x3 _ x1x3x4 = ÄÍÔ.
Определение. Длиной ДНФ назовем число ее конъюнкций, а рангом ДНФ сумму рангов конъюнкций.
Пример. Длина ДНФ из предыдущего примера равна трем, а ранг восьми.
Будем применять обозначение ДНФ f , если захотим отметить, что ДНФ представляет булеву функцию f(x1; : : : ; xn).
Очевидно, что совершенная ДНФ является частным случаем ДНФ, все конъюнкции которой полные. Любая ДНФ может быть преобразована в совершенную ДНФ с использованием основных равносильностей законов склеивания и поглощения конъюнкций.

43
8.2. Преобразование ДНФ в совершенную ДНФ
Алгоритм преобразования ДНФ в совершенную ДНФ (основан на законах склеивания y = xy _ xy и идемпотентности x _ x = x).
Начало: задана ДНФf функции f(x1; : : : ; xn).
Шаг 1 : рассматриваем очередную конъюнкцию K исходной ДНФf . Åñëè все конъюнкции исчерпаны, идем на конец.
Шаг 2 : если конъюнкция K не является полной, то выбираем перемен-
íóþ xi, которая не входит в K, и по закону склеивания заменяем K на дизъюнкцию двух конъюнкций: K = Kxi _ Kxi (в таком применении бу-
дем называть его законом расклеивания соседних конъюнкций ). Если полученные слагаемые не являются полными конюнкциями, то применяем к каждой из них закон расклеивания (шаг 2) до тех пор, пока не получим из конъюнкции K дизъюнкцию полных конъюнкций. Идем на шаг 1.
Конец: на основании закона идемпотентности приводим подобные среди одинаковых конъюнкций получаем СовДНФ функции f(x1; : : : ; xn).
Пример. Пусть ДНФf = x1x2 _ x1x2 _ x3, n = 3. Применим закон расклеивания к каждой конъюнкции:
x1x2 = x1x2x3 _ x1x2x3, x1x2 = x1x2x3 _ x1x2x3,
x3 = x1x3 _ x1x3 = x1x2x3 _ x1x2x3 _ x1x2x3 _ x1x2x3.
В последней строке подчеркнуты конъюнкции, совпадающие с полученными ранее. По закону идемпотентности они не войдут в совершенную ДНФ, которая примет вид
СовДНФf = x1x2x3 _ x1x2x3 _ x1x2x3 _ x1x2x3 _ x1x2x3 _ x1x2x3:
8.3. Элементарная конъюнкция и интервал
Утверждение о конъюнкции и интервале. Каждая элементарная конъюнкция K ранга r может быть задана интервалом IK ранга r. Каждый интервал ранга r задает элементарную конъюнкцию ранга r.
Доказательство (конструктивное).
Рассмотрим произвольную конъюнкцию K ранга r: K = xci11 : : : xcirr : Построим характеристическое множество MK1 .
MK1 = na1 : : : an : aci11 : : : acirr = 1o = na1 : : : an : aci11 = 1; : : : ; acirr = 1o :
Следовательно, для компонент с номерами ij, j = 1; : : : ; r, должно выполняться условие acijj = 1, что, как было показано ранее, эквивалентно

44
условию aij = cj. Остальные компоненты могут принимать любые значе- ния. Это означает, что множество MK1 является интервалом, у которого r
компонент являются внешними, а остальные n r внутренними. Рассмотрим произвольный интервал I ранга r. Пусть его компоненты с
номерами i1; : : : ; ir являются внешними и равны соответственно c1; : : : ; cr. Åñëè I рассматривать как характеристическое множество Mf1 булевой функ- öèè f(x1; : : : ; xn), то из определения интервала следует, что f(x1; : : : ; xn)
принимает на наборе a1; : : : ; an значение 1, если и только если ai1 = c1, : : :, air = cr, то есть если и только если aci11 = 1, : : :, acirr = 1. Отсюда
f(x1; : : : ; xn) = xci11 : : : xcirr :
Таким образом, интервал IK, задающий элементарную конъюнкцию K ранга r, имеет следующий вид:
если переменная xi не входит в K, òî i-я компонента интервала IK является внутренней;
иначе i-я компонента является внешней, она равна 0, если переменная
xi входит в конъюнкцию K с инверсией, и равна 1, если переменная xi входит в K без инверсии.
Примеры. Пусть X = fx1; x2; x3; x4g. Рассмотрим три конъюнкции раз-
ных рангов и их задание интервалами, которые представим троичными векторами и на матрице Грея (здесь и везде далее конъюнкции и задающему ее интервалу будем присваивать один и тот же номер).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
I2 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
K1 = x1x2x3x4; I1 = 1 1 1 0; |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
I1 |
||||||||||
K2 = x3x4; |
|
I2 = 0 1: |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 2 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Конъюнкция K3 = 1 задается интервалом I3 |
= |
|
, òî åñòü âñåì áóëå- |
||||||||||||||||
вым пространством B4. Результаты можно |
|
|
|
|
|
|
|
|
|
конъюнкции |
|||||||||
|
|
|
|
|
проверить построением харак- |
||||||||||||||
теристических множеств M1 конъюнкций. Так множество M1
K2 = x3x4 (согласно определению конъюнкции) состоит из всех векторов,
в которых третья компонента принимает значение 0, четвертая 1, а зна- чения остальных компонент произвольны, значит M1 = 0 1.
Это взаимно-однозначное соответствие между элементарной конъюнкцией и интервалом позволяет рассматривать, например, закон склеивания соседних конъюнкций xy _ xy = y и операцию склеивания соседних интер-
валов Ixy [ Ixy = Iy как один и тот же закон, сформулированный на двух разных языках.

45
8.4. ДНФ и достаточное множество интервалов
Рассмотрим ДНФf = K1 _ : : : _ Km. По определению дизъюнкции, булева функция f(x1; : : : ; xn) принимает значение 1 тогда и только тогда, когда хотя бы одна из конъюнкций K1; : : : ; Km принимает значение 1. Это означает, что соответствующие интервалы I1; : : : ; Im образуют множество, достаточное для функции f(x1; : : : ; xn). Таким образом и в этом случае
можно пользоваться двумя параллельными языками: языком ДНФ и языком интервалов. Последний оказывается наиболее наглядным при задании булевых функций матрицами Грея.
8.4.1. Построение матрицы Грея по ДНФ
Исходя из предыдущих рассуждений о ДНФ и достаточном множестве интервалов, построение матрицы Грея булевой функции f(x1; : : : ; xn) ïî åå ÄÍÔf = K1 _ : : : _ Km сводится к выделению на матрице интервалов I1; : : : ; Im, задающих элементарные конъюнкции K1; : : : ; Km.
Пример. Построим матрицу Грея булевой функции f(a; b; c; d; e) ïî åå
ÄÍÔf = a c _ a b d _ c d e: K1 K2 K3
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
e |
d |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I1 |
|||
|
|
|
|
|
|
|
- |
|
a |
|
|
|
R@ |
|
|
||
b |
|
|
|
|
|
|||
|
|
|
|
|
||||
|
|
|
@ |
|
|
|
|
|
|
|
I3 |
|
|
|
I2 |
|
|
В частности, законы склеивания, обобщенного склеивания и поглощения могут быть продемонстрированы на матрицах Грея следующим образом.
Закон склеивания: |
|
|
|
|
- x y |
= |
|
- y |
||||||||||
|
|
|
|
|
|
|
|
y |
|
|
|
|
y |
|
|
|||
|
_ |
|
|
|
|
|
x |
|
|
|
|
|
x |
|
|
|
||
x y |
|
x y = y |
|
|
|
|
|
- x y |
|
|
- y |
|||||||
Закон поглощения: |
|
|
|
- y |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
y |
|
|
x y |
_ |
y = y |
|
|
|
|
|
-x y |
= |
|
|
|
|
|
||||
|
|
|
|
|
|
x |
|
|
y |
|
x |
|
|
y |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
склеивания: |
|
|
|
|
|
- x z |
= |
|
|
- x z |
||||||||
Закон обобщенного |
|
|
z |
|
|
|
z |
|
||||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
x |
|
|
|
|||
x y |
|
x z = x y |
|
x z |
|
|
|
|
|
- x y |
|
|
y z |
|||||
_ |
_ |
_ |
y z |
|
|
|
|
|
|
|
- x y |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
R@ |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
@ |
|
|
|

46
8.4.2. Построение ДНФ по матрице Грея
Пусть булева функция f(x1; : : : ; xn) задана матрицей Грея. Выделим на ней достаточное множество интервалов. Запишем дизъюнкцию элементар-
ных конъюнкций, заданных этими интервалами получим ДНФ f .
Пример. Рассмотрим булеву функцию пяти переменных, заданную матрицей Грея.
I1 |
|
c |
|
|
|
d |
- I3 |
|
|
HH |
|
|
|
|
HY |
|
e |
|
|
|
|
|
- |
|
|
|
I4 |
|
|
|
|
|
- I2 |
|
b |
|
|
||
a |
|
_ a b c e _ a b c d e |
_ a b: |
|
ÄÍÔf = a c d e |
||||
|
K1 |
K2 |
K3 |
K4 |
В подразделе 3.3 было показано, что булева функция может быть задана различными достаточными множествами интервалов. Из этого следует, что функция в общем случае может быть задана различными ДНФ.
Пример. Рассмотрим функцию из предыдущего примера.
I1 |
|
|
|
|
d |
c |
|
|
|
|
|
HH |
|
|
|
- I3 |
|
|
|
||||
HY |
|
|
|
|
|
|
|
||||
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
- I |
|
|
|
|
||
b |
|
@ |
|
|
2 |
|
|
|
|||
a |
R@ |
I4 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
ÄÍÔ0 = c d e |
_ |
a c e |
_ |
a b c d e |
_ |
a b: |
|
||||
|
f |
K1 |
K2 |
|
K3 |
K4 |
|||||
|
|
|
|
|
|
|
|
||||
Заметим, что ДНФ0
f проще, чем ДНФf , так как при одинаковой длине
ÄÍÔ0
f имеет меньший ранг (13 вместо 15).
8.5. Построение ДНФ по формуле
Пусть булева функция f(x1; : : : ; xn) задана формулой. Применим к ней
разложение Шеннона по любой переменной (наиболее предпочтительным, как правило, является выбор чаще встречающейся переменной, так как появление большого числа констант приводит к значительному упрощению

47
формул). Если коэффициенты полученной формулы не являются ДНФ, то применим разложение Шеннона к коэффициентам, и так далее до тех пор, пока все очередные коэффициенты не превратятся в ДНФ, затем раскроем
скобки получим ДНФf .
Пример. Рассмотрим функцию трех переменных
f(x; y; z) = (x ! yz)=(x z):
Разложим ее по переменной x (она встречается в формуле чаще y и так же часто как z):
f(x; y; z) = x [(1 ! yz)=(1 z)] _ x [(0 ! yz)=(0 z)] =
[ упростим выражение, используя свойства 0 и 1 для дизъюнкции с исклю- чением (0 a = a, 1 a = a), для штриха Шеффера (1=a = a) è äëÿ
импликации (0 ! a = 1, 1 ! a = a); способ получения этих свойств был рассмотрен в подразделе 4.4 ]
= x [yz=z] _ x [1=z] = x [yz=z] _ x z =
[ разложим коэффициент при x по переменной z (она встречается в подформуле чаще y) ]
= x [z (y1=1) _ z (y0=0)] _ x z = x [z (y=0) _ z (0=1)] _ x z =
[ используем свойство 0 для штриха Шеффера ( 0=a = 1) и закон исклю- ченного третьего ]
= x [z 1 _ z 1] _ x z = x [z _ z] _ x z = x _ x z:
Полученная формула является ДНФ.
8.6. Упражнения
Упр.1. На матрице Грея для пяти переменных построить интервалы, задающие конъюнкции:
K1 = x1x3x5; K2 = x2x4; K3 = x1x2x3x4x5; K4 = x1, K5 = x2x3x4:
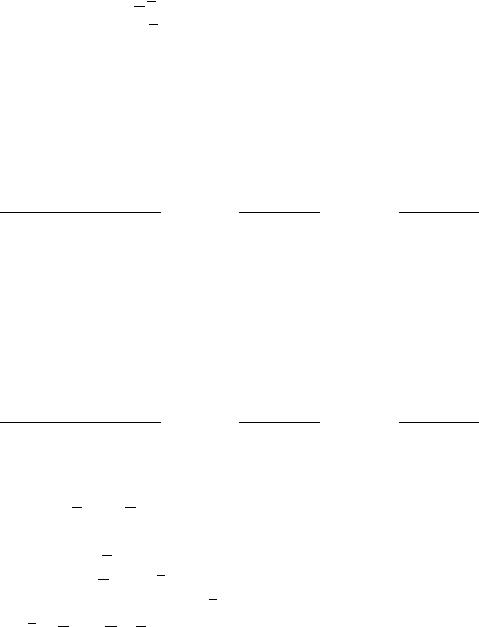
Упр.2. Записать конъюнкции, заданные интервалами I1 I6.
c
|
|
|
|
|
e |
d |
? |
I4 |
d c |
? |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I3 |
|
|
I6 |
||||
b |
|
|
|
|
|
6 |
b |
|
|
6 |
||
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
? |
|
|
|||
a |
|
? |
? |
|
|
a |
|
|
||||
|
|
|
|
|
|
|
|
|
||||
I1 |
I2 |
I5 |
48
Упр.3. Преобразовать ДНФ1 ÄÍÔ3 в совершенные ДНФ и проверить результат построением мàòðèö Ãðåÿ:
ÄÍÔ1 = a d _ b c d _ a b d,
ÄÍÔ2 = a b _ a c _ a b,
ÄÍÔ3 = a d _ b d _ a b.
Упр.4. Построить ДНФ из конъюнкций ранга 3 и менее по матрицам
Ãðåÿ. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
c |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
d |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
||||||
Упр.5. На каждой матрице Грея выделить достаточное множество максимальных интервалов и построить по ним ДНФ.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
c |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
d |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
||||
Упр.6. Построить ДНФ по формулам F1 F6 и проверить правильность вычислений построением таблиц истинности.
F1 = x ! y z ! x y; F2 = x y - (x z);
F3 = y # (x yz) ,! y _ z; F4 = x y=(z y) _ (x t y),
F5 = y ! x t ! (y x) ! y t _ x y z, F6 = zt y ! (x # z t).
9. Сокращенная, кратчайшая, минимальная и безызбыточная ДНФ
9.1. Импликанты функции и сокращенная ДНФ
Рассмотрим булевы функции f(x1; : : : ; xn) è g(x1; : : : ; xn). Определение. Булева функция g(x1; : : : ; xn) называется импликантой
функции f(x1; : : : ; xn), åñëè
g(x1; : : : ; xn) ! f(x1; : : : ; xn) 1:

49
Òàê êàê x ! y = 0 только на наборе 10, то для того, чтобы функция g(x1; : : : ; xn) была импликантой функции f(x1; : : : ; xn) достаточно, чтобы на всех тех наборах , на которых g( ) = 1, функция f(x1; : : : ; xn) также принимала значение 1.
Примеры. Пусть функция f(x; y; z) задана матрицей Грея (левая ма-
трица на рисунке). Функция g(x; y; z) и конъюнкции K1 = x y z, K2 = z (три правые матрицы) ее импликанты.
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
y |
|
|
|
y |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x |
x |
|
x |
|
x |
|
|||||||||||||||||||||||||||||
|
f(x; y; z) |
|
g(x; y; z) |
|
|
K1 = |
|
y z |
|
|
K2 = z |
|
|||||||||||||||||||||||
|
|
|
|
x |
|
||||||||||||||||||||||||||||||
Очевидно, что если K любая конъюнкция ДНФf , òî K является импликантой функции f(x1; : : : ; xn) и задается допустимым для функции f(x1; : : : ; xn) интервалом IK.
Определение. Элементарная конъюнкция K называется простой им-
пликантой функции f(x1; : : : ; xn), если она является импликантой этой функции, и не существует другой конъюнкции K0, которая является им-
пликантой функции f(x1; : : : ; xn) и поглощает конъюнкцию K. Примеры. Рассмотрим функцию f(x; y; z) из предыдущего примера.
Конъюнкция K2 = z простая импликанта данной функции, а конъюнция K1 = x y z импликанта, но не простая, так как она поглощается импликантой K2.
Другими словами, простая импликанта функции это такая импликантаконъюкция, которая не может быть упрощена выбрасыванием из нее переменных, то есть неупрощаемая конъюнкция. Это означает, что всякая простая импликанта K булевой функции f(x1; : : : ; xn) задается максимальным
для этой функции интервалом IK.
Определение. ДНФ, состоящая из всех простых импликант булевой функции f(x1; : : : ; xn), называется сокращенной ДНФ этой функции (или
СокрДНФ f ).
Из определения следует, что сокращенная ДНФ единственна для данной функции, то есть наряду с СовДНФ и СовКНФ она является еще одной канонической формой представления булевой функции.
В общем случае построение сокращенной ДНФ является довольно сложной задачей, которая будет рассмотрена нами далее. Однако для булевой функции небольшого числа аргументов, заданной матрицей Грея, найти сокращенную ДНФ (или, что то же самое, множество всех максимальных

50
интервалов ) довольно просто, и мы уже решали такую задачу для мажоритарной функции в подразделе 3.3, изучая интервальный способ задания булевой функции.
Примеры. Найдем сокращенные ДНФ функций из предыдущего примера: f(x; y; z), g(x; y; z), и функции h(x; y; z).
|
y |
- I2 |
СокрДНФf = z |
|
x y: |
|
|
|
|
|
|
|
|||
|
z |
|
|
|
|
|
|
x |
|
|
K1 |
_ K2 |
|
|
|
|
|
|
|
|
|
|
|
|
@ |
|
|
|
|
|
|
|
R@ |
|
|
|
|
|
|
|
I1 |
|
|
|
|
|
|
|
z y- I2 |
СокрДНФg = y z |
x y |
_ |
x z: |
||
|
|
- I3 |
K1 |
_ K2 |
K3 |
||
|
|
|
|
|
|
|
|
x |
? |
|
|
|
|
|
|
I1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
СокрДНФh сложнее она состоит из шести простых импликант, поэтому для наглядности изображена на двух матрицах Грея:
|
|
z |
y |
|
|
|
|
z |
y |
|
||
|
- I2 |
I5 |
|
- I6 |
||||||||
|
|
|
|
|
|
|
||||||
|
|
|
|
- I3 |
|
|
|
- |
|
|||
x |
|
|
|
x |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
I4 |
||||
|
? |
|
|
|
|
|
|
|
|
|
|
|
|
I1 |
|
СокрДНФh = y z |
_ x z _ x y _ x z _ x y _ y z: |
||||||||
|
|
|
||||||||||
|
|
|
|
|
|
K1 |
|
K2 |
K3 K4 K5 K6 |
|||
Обратим внимание на то, что термин сокращенная относится не к длине ДНФ (она может быть большой, значительно больше длины совершенной ДНФ), а к рангам всех ее конъюнкций ранги неупрощаемых конъюнкций (именно из них состоит сокращенная ДНФ) не могут быть уменьшены.
9.2. Минимальная и кратчайшая ДНФ
Определение. Минимальной ДНФ (МинДНФf ) булевой функции f(x1; : : : ; xn) называется ДНФ наименьшего ранга из всех ДНФ, задающих функцию f(x1; : : : ; xn).
Определение. Кратчайшей ДНФ (КратДНФ f ) булевой функции f(x1; : : : ; xn) называется ДНФ наименьшей длины из всех ДНФ, задающих функцию f(x1; : : : ; xn).
