ТПН лабы

ОСНОВЫ ТЕОРИИ ПЕРЕНОСА НЕЙТРОНОВ

z1 ≤ z ≤ c −(2,5γ11 ), выражение для плотности потока нейтронов (3.8) примет вид

Это выражение позволяет по измеренному потоку нейтронов вдоль оси z призмы определить коэффициент релаксации γ11 , а затем по формуле

(3.7) рассчитать значение χ2 .

Следует заметить, что коэффициент релаксации γ11 определяется

по той части распределения плотности потока, которая соответствует экспоненциальному закону. Именно с таким ходом зависимости плотно-

сти нейтронов связаны названия экспоненциальный реактор, экспоненциальные опыты, теория экспоненциального опыта.

Примером другой геометрии экспоненциального реактора служит цилиндр с экстраполированным радиусом R и плоским источником в начале координаты z. В этом случае поток при больших величинах z есть

Результаты измерений потока вдоль оси z, выполненных с помощью небольших фольг или счетчиков, сопоставляются с равенствами (3.6), (3.10), откуда можно вычислить коэффициент релаксации γ11 . Используя

уравнения (3.7), (3.11) и размеры колонны, можно найти параметр χ2 .

3.2.2. Ожидаемое распределение плотности нейтронов в экспоненциальном реакторе

Чтобы понять, какая информация может быть получена из экспоненциальных опытов, обсудим некоторые возможные частные случаи на примере определения квадрата длины диффузии (в этом случае

χ2 ≡ −1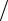L2 ) в тепловой колонне в виде прямоугольной призмы с цен-

трально размещенным точечным источником тепловых нейтронов [1]. В этом случае также приходят к уравнениям (3.7) и (3.9).

72

ОСНОВЫ ТЕОРИИ ПЕРЕНОСА НЕЙТРОНОВ

3.2.3.1. Определение эффективного поперечного сечения поглощения

При вычислении Σa используют метод кадмиевого отношения,

суть которого заключается в следующем.

Поскольку элемент индий поглощает как тепловые, так и резонансные нейтроны, то в случае, если он один используется как детектор нейтронов, можно измерить только суммарный поток тепловых и резонансных нейтронов. Однако, если индиевая фольга покрывается слоем кадмия, поглощающим все нейтроны вплоть до пороговой энергии кадмия ECd = 0,4 эВ, то

активация индиевой фольги измеряет поток одних резонансных нейтронов. Кадмиевое отношение есть отношение результатов двух таких измерений общей активности At + Ar (без кадмиевого экрана) и активности, обуслов-

леннойтолькорезонанснымпоглощением Ar (скадмиевымэкраном):

Cd Ar

Согласно теории, отношение At Ar =RCd −1 равно:

где выделен индиевый резонансный интеграл. Это уравнение представляет отношение потока тепловых нейтронов к потоку резонансных. Плотность замедления q входит в уравнение баланса тепловых нейтронов

DΦ0 − ΣaΦ0 + q = 0,

атак как в стационарном критическом состоянии пространственное распределение потока тепловых нейтронов подчиняется волновому уравнению

Φ0 + χ2Φ0 = 0 ,

то отсюда следует выражение для плотности замедления

74

ОСНОВЫ ТЕОРИИ ПЕРЕНОСА НЕЙТРОНОВ

Следует отметить очень подробное изложение различных методов определения параметров переноса в неразмножающих средах в работе [3]

§3.3. Теория экспоненциального опыта в определении параметров переноса быстрых нейтронов

Для создания реактора на тепловых нейтронах требуется введение в активную зону большой доли замедлителя. Последний должен обладать малым поглощением нейтронов и высокой замедляющей способностью, т.е. свойствами, обеспечивающими достаточно малые длины за-

медления τT или возраст тепловых нейтронов τT . Важность этой характеристики можно видеть из уравнения критичности Ферми (3.15)

где B2 − лапласиан, Pτ ,PL − вероятности избежать утечки быстрыми

нейтронами в процессе замедления и тепловыми нейтронами в процессе диффузии. Видно, что вероятность избежать утечек при замедлении полностью определяется возрастом тепловых нейтронов.

Впервые понятие возраста было введено при попытке аналитиче-

ского решения кинетического уравнения Больцмана, имеющего в операторной форме следующий вид [4]

имеют смысл интеграла упругих и неупругих соударений или скорости замедленияиинтеграладеленияилискоростигенерациинейтроновделения

76

ОСНОВЫ ТЕОРИИ ПЕРЕНОСА НЕЙТРОНОВ

Как известно в асимптотической области в случае замедления без поглощения имеет место спектр Ферми

Вблизи u = 0 плотность соударений меняется весьма заметно. Однако

интегральная функция плотности замедления нейтронов

при слабом поглощении меняется незначительно и с интегралом соударений связано соотношением

В асимптотической области, где плотность упругих соударений практически не меняется (см. 3.20), можно записать

где

ζ = ∫u ∞∫W0 (u′′− u′)du′′du′

u−q u

есть среднее приращение летаргии за одно соударение в смеси замедляющих ядер.

Возрастное приближение (3.23) распространяется на всю область замедления [0,u].

Тогда интеграл соударений можно записать как

S0Φ ΦΣs − ζ ∂ΦΣs ∂u

и уравнение (3.19) преобразуется в уравнение замедления в возрастном приближении, выраженное через глобальный поток Ф

78

Глава 3. ТЕОРИЯ ЭКСПОНЕНЦИАЛЬНОГО ОПЫТА

Таким образом, вводя поток замедления в приближении (3.23) удалось интегро-дифференциальное уравнение (3.19) свести к дифференциальному уравнению в частных производных, т.е. заметно упростить задачу.

Выразим последнее уравнение замедления через плотность замедления (3.23)

уравнение (3.25) преобразуется в стационарное уравнение замедления в возрастном приближении через переменную возраста

Для нестационарной задачи замедления в возрастном приближении че-

рез переменную возраста уравнение примет вид

обычно рассматривают следующие стационарные задачи замедления:

79

ОСНОВЫ ТЕОРИИ ПЕРЕНОСА НЕЙТРОНОВ

а) безпоглощения, когда L2 (τ) = ∞ иуравнение(3.27) сводитсяквиду

с начальным условием j (r ,0)= f (r );

б) с поглощением, когда L2 (τ)< ∞, тогда (3.27) можно записать как

с тем же начальным условием.

Последнее уравнение можно привести к виду (3.29), если представить функцию потока замедления в виде произведения

j (r ,τ)= ϕ(τ) j0 (r ,τ),

где j0 (r ,τ)−решение для непоглощающей среды; ϕ(τ)−вероятность

нейтрону избежать поглощения в процессе замедления до возраста τ. Уравнение типа (3.29) является частным случаем нестационарного

уравнения в однородной бесконечной среде с коэффициентом температуропроводности равным единице и отсутствии стоков тепла. Фунда-

ментальное решение или функция Грина этого уравнения для различных источников (плоский, линейный, точечный) известно:

Знаменитое уравнение возраста (3.29) было впервые получено Э. Ферми в 1942 г. Приблизительно через 1,5 года это уравнение независимо вывел Я.Б. Зельдович.

80