
- •«Национальный исследовательский
- •Методические указания к выполнению контрольной работы № 1 введение в анализ Предел функции
- •Второй замечательный предел
- •Варианты контрольных заданий для контрольной работы № 1 Введение в анализ
- •Методические указания к выполнению контрольной работы № 2
- •Основные правила дифференцирования
- •Правило дифференцирования сложной функции
- •Дифференцирование функций, заданных параметрически
- •Производная неявной функции
- •Геометрический смысл производной
- •Правило отыскания наибольшего и наименьшего значения функции
- •Наклонные и горизонтальные асимптоты
- •Варианты контрольных заданий для контрольной работы № 2
- •Математический анализ 1
- •080200 «Mенеджмент»
- •Отпечатано в Издательстве тпу в полном соответствиис качеством предоставленного оригинал-макета
Правило отыскания наибольшего и наименьшего значения функции
Найти первую производную и все критические точки
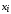 ,
принадлежащие
,
принадлежащие .
.Вычислить значения
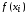 .
.Вычислить значения функции на концах промежутка.
Сравнить все полученные значения функции
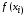 ,
, ,
, и выбрать среди них наибольшее и
наименьшее.
и выбрать среди них наибольшее и
наименьшее.
Задача.
Найти наибольшее и наименьшее значения
функции
 на промежутке
на промежутке .
.
Решение.
Необходимое
условие экстремума
 ,
поэтому
,
поэтому ,
а корни уравнения
,
а корни уравнения являются критическими точками, но
промежутку принадлежит только
являются критическими точками, но
промежутку принадлежит только .
Найдем теперь
.
Найдем теперь и на концах промежутка
и на концах промежутка и
и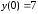 .
Среди них самое большое 23, самое меньшее
7.
.
Среди них самое большое 23, самое меньшее
7.
Выпуклость и вогнутость кривой. Точки перегиба
Пусть
кривая задана функцией
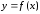 .
.
Определение
1.
Кривая называется выпуклой вверх (вниз)
на отрезке
 ,
если все точки кривой находятся ниже
(выше) любой касательной к графику
функции.
,
если все точки кривой находятся ниже
(выше) любой касательной к графику
функции.
Определение
2.
Точка

 ,
отделяющая вогнутую часть от выпуклой,
называется точкой перегиба графика
функции
,
отделяющая вогнутую часть от выпуклой,
называется точкой перегиба графика
функции .
.
Теорема.
Если функция
 дважды дифференцируема на некотором
промежутке, причем
дважды дифференцируема на некотором
промежутке, причем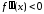 для любого
для любого из этого промежутка, то на этом промежутке
график функции выпуклый, если
из этого промежутка, то на этом промежутке
график функции выпуклый, если ,
то график вогнутый.
,
то график вогнутый.
Из
теоремы следует, что для нахождения
промежутков (выпуклости) вогнутости
надо найти вторую производную функции
и определить промежутки, где она
положительна (отрицательна). Необходимым
условием существования точки перегиба
является обращение в нуль второй
производной или ее отсутствие в точке
 ,
то есть условие
,
то есть условие или
или .В
случае выполнения одного из этих условий
точка
.В
случае выполнения одного из этих условий
точка
 называется критической точкой второго
рода.
называется критической точкой второго
рода.
Достаточным
условием того, что точка
 -
точка перегиба является смена знака
второй производной при переходе через
критические точки второго рода.
-
точка перегиба является смена знака
второй производной при переходе через
критические точки второго рода.
Правило нахождения интервалов выпуклости, вогнутости и точек перегиба функции.
Указать область определения функции.
Найти критические точки второго рода, принадлежащие области определения функции.
Определить знак второй производной в каждом интервале области определения между соседними критическими точками.
По знаку
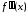 установить интервалы выпуклости,
вогнутости и по смене знака второй
производной в окрестности точки –
наличие или отсутствие точки перегиба.
установить интервалы выпуклости,
вогнутости и по смене знака второй
производной в окрестности точки –
наличие или отсутствие точки перегиба.
Асимптоты графика функции
Определение.
Асимптотой графика функции называется
прямая, к которой неограниченно
приближается график функции при
 или
или .
.
Различают вертикальные, горизонтальные и наклонные асимптоты.
Вертикальные асимптоты. Прямая
 называется вертикальной асимптотой,
если при
называется вертикальной асимптотой,
если при хотя бы один из односторонних пределов
в точке
хотя бы один из односторонних пределов
в точке бесконечен, т.е.
бесконечен, т.е. или
или т. е. в точке
т. е. в точке функция терпит разрыв второго рода.
функция терпит разрыв второго рода.
Задача.
Найти вертикальные асимптоты функции
 .
.
Решение.
При
 и
и функция не определена. Найдем односторонние
пределы
функция не определена. Найдем односторонние
пределы при
при .
.
 ,
, ;
; ,
, .
.
Следовательно,
 ,
, вертикальные асимптоты графика.
вертикальные асимптоты графика.
Наклонные и горизонтальные асимптоты
Определение.
Прямая
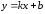 называется наклонной асимптотой графика
функции
называется наклонной асимптотой графика
функции при
при ,если
эту функцию можно представить в виде
,если
эту функцию можно представить в виде ,
,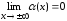 ,
т. е. разность междуординатами
точек кривой и асимптоты при
,
т. е. разность междуординатами
точек кривой и асимптоты при
 есть бесконечно малая величина.
есть бесконечно малая величина.
Теорема. Для того, чтобы график функции имел наклонную асимптоту, необходимо и достаточно, чтобы имели место соотношения:
 ,
,
 ,
причем эти пределы могут быть неравными
при
,
причем эти пределы могут быть неравными
при и при
и при .
Если
.
Если ,
, ,
получаем горизонтальную асимптоту
,
получаем горизонтальную асимптоту .
Таким образом, прямая
.
Таким образом, прямая является горизонтальной асимптотой
кривой
является горизонтальной асимптотой
кривой ,
если
,
если .
.
Задача
2.
Найти асимптоты графика функции
 .
.
Решение.  . Вычислим
. Вычислим
 =
=
= ,
, .
.
Найдем
 :
: .
.
Получим
уравнение асимптоты
 ;
убедимся, что утверждение теоремы
выполняется. Преобразуем функцию,
выделив целую часть.
;
убедимся, что утверждение теоремы
выполняется. Преобразуем функцию,
выделив целую часть.
 ,
где
,
где ,
,
Кроме
того, функция имеет вертикальную
асимптоту
 ,
т. к.
,
т. к.

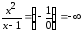 ,
,
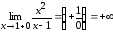 .
.
Задача
3. Найти
асимптоты графика функции
 .
.
Решение.
Найдем
 .
При
.
При функция
функция терпит разрыв второго порядка, т. к.
терпит разрыв второго порядка, т. к.
 .
.
Таким
образом,
 является вертикальной асимптотой.
является вертикальной асимптотой.
Найдем горизонтальные асимптоты.
 ,
следовательно,
,
следовательно,
 является горизонтальной асимптотой.
является горизонтальной асимптотой.
Общая схема исследования функции
Найти область определения функции, исследовать ее поведение на границах области определения.
Найти точки разрыва и установить их характер с помощью односторонних пределов.
Исследовать периодичность, четность (нечетность), найти точки пересечения графика с осями координат.
Найти интервалы монотонности и экстремумы функции.
Найти интервалы выпуклости, вогнутости и точки перегиба графика функции.
Найти асимптоты графика.
Построить график, используя результаты исследования.
Задача
4. Провести
полное исследование и построить график
функции
 .
.
Найдем область определения
 .
из условия
.
из условия ,
, ,
, ,
следовательно,
,
следовательно,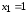 ,
,
 – точки разрыва. Найдем односторонние
пределы:
– точки разрыва. Найдем односторонние
пределы:
 ,
,
 ,
,
 ,
,
 .
.
Отсюда
следует, что
 и
и – точки разрыва второго рода, и
– точки разрыва второго рода, и – вертикальные асимптоты.
– вертикальные асимптоты.
Для установления симметрии графика функции
найдем
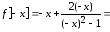
 =
–
=
– ,
это означает, что
,
это означает, что – нечетная функция, и ее график симметричен
относительно начала координат. Достаточно
провести ее исследование для
– нечетная функция, и ее график симметричен
относительно начала координат. Достаточно
провести ее исследование для .
Очевидно, что функция не является
периодической. Точка О (0,0) является
единственной точкой пересечения с осями
координат, т.к.
.
Очевидно, что функция не является
периодической. Точка О (0,0) является
единственной точкой пересечения с осями
координат, т.к. .
.
Первая производная:
 ,
,
Критические
точки найдем из условий
 ,
,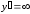 .
.
а)
 ,
, ,
,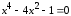 ,
, .
.
Решая
биквадратное уравнение, найдем
 .
.
б)
 ,
, ,
, ,
, .
.
Таким
образом, критические точки функции: ,
, ,
а точки
,
а точки не входят в область определения,
следовательно, не являются критическими
точками. Проверим критические точки на
экстремум по первому признаку.
не входят в область определения,
следовательно, не являются критическими
точками. Проверим критические точки на
экстремум по первому признаку.
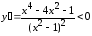 ,
при
,
при ,
, ,
при
,
при
Так
как производная меняет знак при переходе
через критическую точку, то в точке
 функция имеет минимум. Составим
таблицу.
функция имеет минимум. Составим
таблицу.
|
|
0 |
(0, 1) |
1 |
(1; 2.05) |
2,05 |
(2,05,
|
|
|
0 |
|
не сущ. |
|
(min) 3,4 |
|
|
|
0 |
– |
не сущ. |
– |
0 |
+ |
Найдем
 .
Критические
.
Критические
точки
второго рода найдем из условия
 ,
, ,
, ;
при
;
при ,откуда
,откуда .
Так как
.
Так как не входят в область определения функции,
то
не входят в область определения функции,
то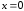 единственная критическая точка. Проверим
знак второй производной при переходе
через точку
единственная критическая точка. Проверим
знак второй производной при переходе
через точку
 при
при ,
,
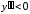 при
при
 .
. меняет знак с «+» на «–», значит,
меняет знак с «+» на «–», значит,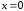 – точка перегиба, и график меняет
вогнутость на выпуклость при переходе
через критическую точку. Итак, в (0, 1)
функция выпукла, а в
– точка перегиба, и график меняет
вогнутость на выпуклость при переходе
через критическую точку. Итак, в (0, 1)
функция выпукла, а в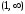 – вогнута.
– вогнута.
Найдем асимптоты. Наклонные асимптоты имеют вид:
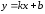 ;
;
 =
=
 ,
,

 ,
, ,
,
отсюда
уравнение наклонной асимптоты
 .
Горизонтальные асимптоты отсутствуют,
а вертикальные были найдены в п. 2.
.
Горизонтальные асимптоты отсутствуют,
а вертикальные были найдены в п. 2.
По результатам исследования построим график. Так как
функция
нечетная, то можно построить график для
 и отобразить его симметрично начала
координат.
и отобразить его симметрично начала
координат.

