
- •«Национальный исследовательский
- •Методические указания к выполнению контрольной работы № 1 введение в анализ Предел функции
- •Второй замечательный предел
- •Варианты контрольных заданий для контрольной работы № 1 Введение в анализ
- •Методические указания к выполнению контрольной работы № 2
- •Основные правила дифференцирования
- •Правило дифференцирования сложной функции
- •Дифференцирование функций, заданных параметрически
- •Производная неявной функции
- •Геометрический смысл производной
- •Правило отыскания наибольшего и наименьшего значения функции
- •Наклонные и горизонтальные асимптоты
- •Варианты контрольных заданий для контрольной работы № 2
- •Математический анализ 1
- •080200 «Mенеджмент»
- •Отпечатано в Издательстве тпу в полном соответствиис качеством предоставленного оригинал-макета
Варианты контрольных заданий для контрольной работы № 1 Введение в анализ
Найти указанные пределы, не пользуясь правилом Лопиталя:
1.1.
а)
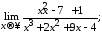 б)
б) в)
в)
г)
 д)
д)

1.2.
а)
 б)
б)
 в)
в)
г)
 д)
д)
1.3.
а)
 б)
б) в)
в)
г)
 д)
д)
1.4.
а)
 б)
б) в)
в) г)
г)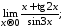 д)
д)
1.5.
а)
 б)
б) в)
в)
г)
 д)
д)
1.6.
а)
 б)
б) в)
в)
г)
 д)
д)
1.7.
а)
 б)
б) в)
в)
г)
 д)
д)

1.8.
а)
 б)
б) в)
в)
г)
 д)
д)
1.9.
а)
 б)
б) в)
в)
г)
 д)
д)
1.10.
а)
 б)
б) в)
в)
г)
 д)
д)
1.11.
а)
 б)
б) в)
в)
г)
 д)
д)
1.12.
а)
 б)
б) в)
в)
г)
 д)
д)
1.13.
а)
 б)
б) в)
в)
г)
 д)
д)
1.14.
а) б)
б)

в)
 г)
г) д)
д)
1.15.
а)
 б)
б)
в)
 г)
г) д)
д)
1.16.
а)
 б)
б) в)
в)
г)

 д)
д)
1.17.
а)
 б)
б) в)
в)
г)
 д)
д)
1.18.
а)
 б)
б) в)
в)
г)
 д)
д)

1.19.
а)
 б)
б) в)
в)
г)
 д)
д)
1.20.
а)
 б)
б) в)
в)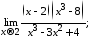
г)
 д)
д)
2.
Исследовать функцию
![]() на непрерывность, найти точки разрыва
функции и определить их тип. Построить
схематический график функции.
на непрерывность, найти точки разрыва
функции и определить их тип. Построить
схематический график функции.
а)
 б)
б) ;
в)
;
в) ;
;
а)
 б)
б) ;
в)
;
в) ;
;
а)
 б)
б) ;
в)
;
в) ;
;
а)
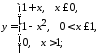 б)
б) ;
в)
;
в) ;
;
а)
 б)
б) ;
в)
;
в) ;
;
а)
 б)
б) ;
в)
;
в) ;
;
а)
 б)
б) ;
в)
;
в) ;
;
а)
 б)
б) ;
в)
;
в) ;
;
а)
 б)
б) ;
в)
;
в) ;
;
а)
 б)
б) ;
в)
;
в) ;
;
а)
 б)
б) ;
в)
;
в)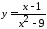 ;
;
а)
 б)
б) ;
в)
;
в) ;
;а)
 б)
б) ;
в)
;
в) ;
;
а)
 б)
б) ;
в)
;
в) ;
;
а)
 б)
б)
 в)
в) ;
;а)
 б)
б) ;
в)
;
в) ;
;
а)
 б)
б) ;
в)
;
в) ;
;
а)
 б)
б) ; в)
; в) ;
;
а)
 б)
б) ;
в)
;
в) ;
;
а)
 б)
б) ;
в)
;
в)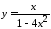 ;
;
Методические указания к выполнению контрольной работы № 2
Производная и правила дифференцирования
1. Пусть
функция
 =
= получила приращение
получила приращение
 ,
соответствующее приращению аргумента
,
соответствующее приращению аргумента .
.
Определение.
Если существует предел отношения
приращения функции
 к вызвавшему его приращению аргумента
к вызвавшему его приращению аргумента ,
при
,
при ,
стремящимся к нулю, т. е.
,
стремящимся к нулю, т. е. ,
то он называется производной функции
,
то он называется производной функции по независимой переменной
по независимой переменной и обозначается
и обозначается ,
или
,
или ,
или
,
или .
.
Функция, имеющая производную, называется дифференцируемой.
Задача
1.
Используя определение, найти производные
функцийа)
 ,
б)
,
б) .
.
Решение:
а) Дадим аргументу
 приращение
приращение и найдем соответствующее значение
функции
и найдем соответствующее значение
функции =
= ,
теперь найдем
,
теперь найдем
![]() и
составим отношение
и
составим отношение
 .
.
Осталось
вычислить
 ,
, .
.
б)
пусть аргумент
 получил приращение
получил приращение ,
новому значению аргумента соответствует
значение функции
,
новому значению аргумента соответствует
значение функции .
.
Найдем
приращение .
. .
.
Тогда

 ,
, .
.
Основные правила дифференцирования
Если
 =соnst,
а функции
=соnst,
а функции ,
, дифференцируемы, то
дифференцируемы, то
1. 4.
4. ;
;
2. ;
5.
;
5. ;
;
3. ;
6.
;
6. .
.
Таблица производных основных элементарных функций
1. ;
10.
;
10. ;
;
2. ,
, ;
11.
;
11. ;
;
3. ;
12.
;
12. ;
;
4. ;
13.
;
13. ;
;
5. ;
14.
;
14. ;
;
6. ;
15.
;
15.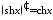 ;
;
7. ;
16.
;
16. ;
;
8. ;
17.
;
17. ;
;
9. ;
18.
;
18. .
.
Правило дифференцирования сложной функции
Если
 и
и ,
т. е.
,
т. е. ,
где
,
где и
и имеют производные, то
имеют производные, то .
Здесь
.
Здесь – промежуточный аргумент. Это правило
распространяется на цепочку из любого
конечного числа дифференцируемых
функций.
– промежуточный аргумент. Это правило
распространяется на цепочку из любого
конечного числа дифференцируемых
функций.
Задача 2. Найти производные функций:
а)
 ,
б)
,
б) ,
в)
,
в) ,
г)
,
г) .
.
Решение: а) представим функцию в табличной форме как сумму степенных функций и затем только найдем производную.
 ,
,

 .
.
б) введем промежуточный аргумент и затем воспользуемся правилом дифференцирования сложной функции.
 ,
,
 ,
, =3
=3
 ;
;
в)
пусть
 ,
где
,
где ,
тогда
,
тогда ,
,
 =
= =
= .
.
Окончательно:
 ,
, ;
;
г) правило 4 можно распространить на любое число сомножителей, если перемножаемые функции дифференцируемы.
 ,
,
 ,
в данном случае
,
в данном случае
 ,
,
 ,
, ,
, ,
,
 ,
,
 ,
,
 .
.
Дифференцирование
сложной показательно-степенной функции
 .
Логарифмическое
дифференцирование
.
Логарифмическое
дифференцирование
Пусть
 и
и – дифференцируемые функции. Чтобы найти
производную функции
– дифференцируемые функции. Чтобы найти
производную функции предварительно прологарифмируем ее по
основанию
предварительно прологарифмируем ее по
основанию :
: ,
теперь воспользуемся правилом 3 и 6
,
теперь воспользуемся правилом 3 и 6
 ,
откуда
,
откуда
 (1)
(1)
Задача
3.
Найти производные функций а)
 ,
б)
,
б)
Решение:
а) воспользуемся формулой (1): Пусть
 ,
, ,
найдем
,
найдем ,
, и подставим в формулу (1):
и подставим в формулу (1):

б)
сначала прологарифмируем
 .
Дифференцируя левую и правую части
равенства, получим:
.
Дифференцируя левую и правую части
равенства, получим:
 ,
теперь найдем
,
теперь найдем

 =
=
 .
.
Метод, основанный на предварительном логарифмировании функции, не требует запоминания формулы и имеет более широкий спектр применения, в частности при дифференцировании большого количества сомножителей.
Задача 4. Найти производные функций:
а)
 ,
б)
,
б) .
.
Решение: а) воспользуемся свойствами логарифмической функции:
 ,
,
 ,
, ,
, .
.
Итак,
 ,
, ,
,
 .
.
