МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

«Национальный исследовательский

ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

УТВЕРЖДАЮ

Директор ИПР

_______________ А.Ю. Дмитриев

«____»_____________2012 г.

МАТЕМАТИЧЕСКИЙ АНАЛИЗ 1

Методические указания и индивидуальные задания для студентов ИПР, обучающихся по направлению080200 «Mенеджмент»

Составители

С.В. Рожкова

В.И. Рожкова

Г.А. Никольская

Г.М. Матвеенко

Семестр	1
Кредиты	4
Лекции, часов	8
Практические занятия, часов	8
Индивидуальные задания	2
Самостоятельная работа, часов	200
Формы контроля	Экзамен

Издательство

Томского политехнического университета

2012

УДК 517

ББК

Математический анализ 1: методические указания и индивидуальные задания для студентов ИПР, обучающихся по направлению 080200 «Mенеджмент» / сост. С.В. Рожкова, В.И. Рожкова, Г.М. Матвеенко, Г.А. Никольская; Томский политехнический университет.– Томск: Изд-во Томского политехнического университета, 2011.– 49с.

Методические указания и индивидуальные задания рассмотрены и рекомендованы к изданию методическим семинаром кафедры высшей математики ФТИ «____» ______2011 года, протокол № ___.

Зав. кафедрой ВМ,

профессор, доктор физ.-мат. наук _________________К.П. Арефьев

Рецензент

Кандидат физико-математических наук,

доцент кафедры ВМ ФТИ

Э.М. Кондакова

© Составление.ГОУ ВПО НИ ТПУ, 2011

© Рожкова С.В., Рожкова В.И., Матвеенко Г.М, Никольская Г.А., составление, 2011

© Оформление. Издательство Томского

политехнического университета, 2011

Методические указания к выполнению контрольной работы № 1 введение в анализ Предел функции

Пусть функция определена в некоторой окрестности точки. Числоназываетсяпределом функции при , стремящемся к, если для любогоможно указать такое число , что для всех , отличных от и удовлетворяющих неравенству, выполняется неравенство.

Если есть предел функции

при стремящемся к то пишут

или при.

Число называетсяпределом функции в точкеслева (пишут ), еслистремится к пределупри , стремящемся к числу так, что принимает только значения, меньшие . Еслипринимает только значения, большие, то пишути называютпределом функции в точке справа.

При вычислении пределов функций используются следующие теоремы:

Если каждая из функций иимеет конечный предел при, то сумма, разность и произведение этих функций также имеет конечный предел, причем

Если, кроме того, , то и частноеимеет конечный предел, причем.

Следствие:

1. Постоянный множитель можно выносить за знак предела

, где .

1. Если и− натуральное число, то

.

Кроме того, при вычислении пределов нужно обратить внимание на то, что элементарные функции непрерывны там, где они определены, т.е.

. (1)

Пример. Найти .

Решение.

Однако, бывают случаи, когда теоремы о пределах суммы, частного и произведения неприменимы, т.к. при вычислении пределов получаются неопределенности .

Для вычисления таких пределов функцию заменяют функцией, принимающей в окрестности точките же значения, что ии определенной в точке. Пределы таких функций равны, т.е.

.

Рассмотрим простейшие приемы раскрытия неопределенностей и нахождения пределов функций.

Неопределенность .

Рассмотрим предел дробно-рациональной функции, когда при и числитель и знаменатель дроби имеют пределы, равные нулю.

Пример. Найти .

Решение.

Непосредственный переход к пределу по формуле (1), дает неопределенность , т.е. функция в точкенеопределена. Для решения задачи поступим следующим образом, разделим числитель и знаменатель дроби на, получим

.

Тогда .

Сформулируем правило.

Для того, чтобы найти предел дробно-рациональной функции в случае, когда при и числитель, и знаменатель дроби имеют пределы, равные нулю, надо числитель и знаменатель дроби разделить наи перейти к пределув полученном выражении. Если и после этого неопределенность сохраняется, то надо произвести повторное деление на.

Пусть − дробь, содержащая иррациональные выражения.

Пример. Найти. .

Решение.

Умножим числитель и знаменатель дроби на выражение . Тогда

Пример. Найти

Решение.

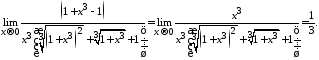
Правило. Чтобы найти предел дроби, содержащей иррациональные выражения, в случае, когда пределы числителя и знаменателя дроби равны нулю, надо освободиться от имеющихся иррациональностей, после этого сделать необходимые упрощения (приведение подобных членов, сокращение одинаковых множителей и т. п.) и перейти к пределу при в полученном выражении.

Замечание. В этом случае используются формулы сокращенного умножения

Неопределенность вида .

Рассмотрим предел при 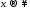отношения двух многочленов

В данном случае теорема о пределе дроби неприменима, т.к. пределы числителя и знаменателя не существуют.

Преобразуем дробь следующим образом:

Очевидно, что

и

Тогда

Правило. Чтобы вычислить предел дробно-рациональной функции в случае, когда при числитель и знаменатель дроби имеют пределы, равные бесконечности, надо числитель и знаменатель дроби разделить навнаибольшей степени, встречающейся в членах дроби, а затем прейти к пределу.

Пример. Найти

Решение.

Пример. Найти

Решение.

Пример. Найти .

Решение.

Пусть − дробь, содержащая иррациональности. Приимеем неопределенность, которую раскрывают по правилу, указанному в предыдущем пункте, т.е. делят числитель и знаменатель дроби нав высшей степени, а затем переходят к пределу при

.

Пример. Найти .

Решение.

Первый замечательный предел

Для раскрытия неопределенности от функций, содержащих тригонометрические и обратные тригонометрические функции используют первый замечательный предел

и следствия из него

.

Примеры.

Замечание. В этом примере использована формула тригонометрии