8.3 Критерий Эппса-Палли

Этот критерий применим при . Малые выборки с<8 при обнаружении отклонений от нормального распределения не дают достоверных результатов.

Многосторонний критерий с высокой мощностью при многих альтернативных гипотезах использует сумму квадратов модулей разности между характеристическими функциями на основе выборочных данных и нормального распределения с весомыми коэффициентами.

По наблюдениям(=1, 2, ...,) вычисляют следующие параметры:

(13)

и

, (14)

где - среднее арифметическое;

- выборочный центральный момент второго порядка;

- объем выборки.

Статистику критерия Эппса-Палли вычисляют по формуле

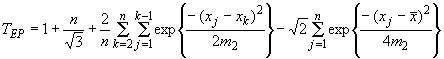. (15)

Порядок значений произволен, но он должен оставаться неизменным в течение всех проводимых вычислений.

Алгоритм вычисления статистики критерия Эппса-Палли представлен на рисунке 8.

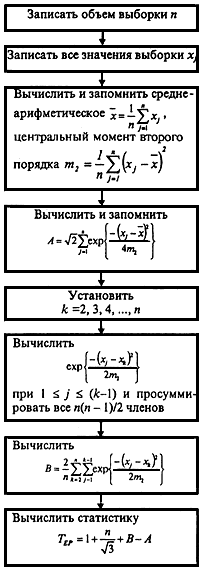
Рисунок 8 - Алгоритм вычисления статистики критерия Эппса-Палли

Нулевую гипотезу отклоняют, если вычисленное значение статистики превышает-квантиль при данных уровне значимостии объеме выборки.-Квантили статистики критерияпри=0,90; 0,95; 0,975 и 0,99 приведены в таблице 12.

Пример 5

Пример применения критерия Эппса-Палли. Таблица 5 содержит серию из 25 значений показателя прочности вискозной нити, измеренной при стандартных условиях в произвольных единицах. Дополнительно даны преобразованные значения, которые рассеяны около прямой линии, нанесенной на бумаге для нормальных вероятностных графиков.

Таблица 5 - Значения показателя прочности вискозной нити

Измеренные значения	Преобразованные значения
147	1,756
186	1,255
141	1,799
183	1,322
190	1,146
123	1,908
155	1,690
164	1,602
183	1,322
150	1,732
134	1,845
170	1,531
144	1,778
99	2,021
156	1,681
176	1,447
160	1,643
174	1,477
153	1,708
162	1,623
167	1,568
179	1,398
78	2,100
173	1,491
168	1,556

На основе данных таблицы 5 вычислено значение статистики критерия =0,612 с использованием калькулятора. Используем таблицу 12 для поиска значения квантиля уровня=0,99 при=25. В таблице установлены следующие значения:

для =20-квантиль равен 0,564;

для =30-квантиль равен 0,569.

С помощью интерполяции значений, приведенных в таблице 12, можно оценить, что -квантиль для=25 будет равен приблизительно 0,567. Вычисленное значениепревышает это критическое значение, поэтому нулевая гипотеза отклоняется при уровне значимости=0,01 для значений.

На основе данных таблицы 5 найдено =0,006. Поскольку это значение менее критического значения для=25, то нулевая гипотеза для преобразованных значенийне отклоняется.

Этот пример подтверждает известный факт, что значения показателя прочности вискозной нити подчиняются логарифмически нормальному закону распределения.

Пример 6

Пример детально описывает процедуру вычисления статистики критерия в соответствии с формулой (15).

Второй столбец таблицы 6 содержит =10 значениям, для которых должен быть проведен критерий Эппса-Палли. Согласно выражениям (13) и (14), получаем=10,4 и=11,858.

Таблица 6 - Значения показателя прочности вискозной нити - вычисление статистики критерия

		=2	=3	=4	=5	=6	=7	=8	=9	=10
											=1, ..., 10
1	4,9	0,9996	0,8977	0,2192	0,2083	0,1684	0,0769	0,0587	0,0304	0,0205	0,5285
2	5,0	-	0,9095	0,2304	0,2192	0,1778	0,0821	0,0629	0,0329	0,0222	0,5407
3	6,5	-	-	0,4421	0,4258	0,3633	0,1977	0,1593	0,0933	0,0673	0,7257
4	10,9	-	-	-	0,9996	0,9895	0,8723	0,8154	0,6668	0,5790	0,9947
5	11,0	-	-	-	-	0,9933	0,8853	0,8303	0,6842	0,5966	0,9924
6	11,4	-	-	-	-	-	0,9312	0,8853	0,7520	0,6668	0,9791
7	12,7	-	-	-	-	-	-	0,9933	0,9312	0,8723	0,8945
8	13,1	-	-	-	-	-	-	-	0,9664	0,9207	0,8575
9	14,0	-	-	-	-	-	-	-	-	0,9895	0,7609
10	14,5	-	-	-	-	-	-	-	-	-	0,7016
Сум- ма	104,0	0,9996	1,8072	0,8916	1,8528	2,6923	3,0455	3,8052	4,1573	4,7350	7,9757
Общая сумма 23,9865

Двойная сумма в третьем члене выражения (15) является конечной серией () подсерий, первая из которых имеет один член, а последняя () член.

Для первой подсерии установлен индекс =2 и единственный член суммы, равный

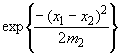, получен при=1. Во второй подсерии установлен индекс=3 и сумма имеет два члена, равные:

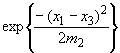и ,

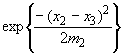которые получены при =1 и=2. Для последней подсерии фиксирован индекс=10, и сумма имеет 9 членов, равные:

,

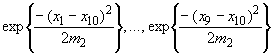которые получены при =1, 2, 3, ..., 9.

Значения членов для -1=9 подсерий перечислены в столбцах 3-11 таблицы 6.

12-й столбец показывает =10 членам суммы в четвертом члене выражения (15).

Для каждого из последних 10 столбцов таблицы 6 вычислены их суммы и указаны внизу столбца.

Все 45 членов, принадлежащих сумме в третьем члене выражения (15), после суммирования дали общую сумму .

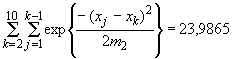Окончательно выражение (15) подсчитано и равно

.

При =10 таблица 12 содержит значение-квантиля для=0,95, равное 0,357. Вычисленное значение=0,2914 не превышает это критическое значение, поэтому в этом примере нулевая гипотеза не отклоняется при уровне значимости=0,05.