Угловое ускорение
Углово́е ускоре́ние — векторная физическая величина, характеризующая быстроту изменения угловой скорости твёрдого тела.
При вращении тела вокруг неподвижной оси, угловое ускорение по модулю равно:
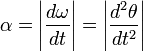
Вектор
углового ускорения α направлен вдоль
оси вращения (в сторону
при
ускоренном вращении и противоположно
—
при замедленном).
При вращении вокруг неподвижной точки вектор углового ускорения определяется как
,
и
направлен по касательной к вектору
в
соответствующей его точке.
. Итак, угловое ускорение равно второй производной от угла поворота по времени или первой производной от угловой скорости по времени. Угловое ускорение измеряется в рад/сек2 .
Криволинейное движение
Криволинейные движения – движения, траектории которых представляют собой не прямые, а кривые линии. По криволинейным траекториям движутся планеты, воды рек.
Криволинейное движение – это всегда движение с ускорением, даже если по модулю скорость постоянна. Криволинейное движение, определяется по формулам
Частным
случаем криволинейного движения –
является движение по окружности. И
определяется по формуле:
где
r
– радиус окружности.
Вектор ускорения при движении по окружности направлен к центру окружности и перпендикулярно вектору скорости.
При
криволинейном движении ускорение можно
представить как сумму нормальной
и
тангенциальной
составляющих:
,
-
нормальное (центростремительное)
ускорение, направлено к центру кривизны
траектории и характеризует изменение
скорости по направлению:
v – мгновенное значение скорости, r – радиус кривизна траектории в данной точке.
-
тангенциальное (касательное) ускорение,
направлено по касательной к траектории
и характеризует изменение скорости по
модулю.
Полное ускорение, с которым движется материальная точка, равно:
.
Кроме центростремительного ускорения, важнейшими характеристиками равномерного движения по окружности являются период и частота обращения.
Угловая скорость (w) – величина, равная отношению угла поворота радиуса, на котором находится вращающаяся точка, к промежутку времени, за который произошел этот поворот:
.
Связь между линейной и угловой скоростями:
v= wr.
Динамика
Дина́мика— раздел механики, в котором изучаются причины возникновения механического движения. Динамика оперирует такими понятиями, как масса, сила, импульс, энергия. В основе Д. лежат три закона Ньютона, из которых как следствия получаются все уравнения и теоремы, необходимые для решения задач Д.
Согласно первому закону (закону инерции) материальная точка, на которую не действуют силы, находится в состоянии покоя или равномерного прямолинейного движения; изменить это состояние может только действие силы. Второй закон, являющийся основным законом Д., устанавливает, что при действии силы F материальная точка (или поступательно движущееся тело) с массой m получает ускорение w, определяемое равенством
mw = F. (1)
Третьим законом является закон о равенстве действия и противодействия (см. Действия и противодействия закон). Когда к телу приложено несколько сил, F в уравнении (1) означает их равнодействующую. Этот результат следует из закона независимости действия сил, согласно которому при действии на тело нескольких сил каждая из них сообщает телу такое же ускорение, какое она сообщила бы, если бы действовала одна.
Основная задача динамики
Исторически деление динамики сложилось следующим образом.
-
Прямая задача динамики: по заданному характеру движения определить равнодействующую сил, действующих на тело.
-
Обратная задача динамики: по заданным силам определить характер движения тела.
Уравнение движения
Уравне́ние движе́ния (уравнения движения) — уравнение или система уравнений, задающие закон эволюции механической или сходной динамической системы (например, поля) во времени[1].(примером может служить Вторй закон Ньютона)
А) Движение точки есть последовательный и непрерывный переход ее через точки пространства, совершающийся с течением времени; такое движение называется абсолютным. Если известен вид и положение траектории в пространстве, то движение точки будет вполне известно, а для этого: 1) надо выбрать на траектории какую-либо постоянную точку so, от которой считать расстояние по кривой; 2) надо условиться, в каком из двух направлений по кривой расстояния считать положительными, и 3) надо знать, какой функцией времени t выражается расстояние s движущейся точки от SO . Пусть s = f(t).
С другой стороны, координаты точек траектории могут быть выражены функциями расстояний точек от SO; пусть х = φ 1(s), у = φ 2(s), z = φ 3(s). Подставив сюда вместо s — функцию f(t), получим уравнения:
x = f1(t); У = f2(t); z = f3(t)
(где f 1(t) = φ(f(t)) θ т. д.)
выражающие закон изменения координат движущейся точки с течением времени. Уравнения эти называются уравнениями движения точки
В) Движения твердых тел. Такое тело, все точки которого сохраняют неизменные расстояния между собою, называется твердым или, вернее, идеально твердым телом, так как все существующие твердые тела деформируются более или менее, смотря по природе их и по величине сил, на них действующих.
Когда известны функции времени, выражающие закон изменения величин х 1, у 1 , z1, θ, ψ, φ, ςо могут быть составлены уравнения Д. всякой точки твердого тела. Пусть координаты этой точки по отношению к неизменно связанным с телом осям суть ξ, η, ς. Οо формулам преобразования координат коорд. х, у, z той же точки по отношению к неподвижным осям могут быть выражены так:
х = х 1 + a1ξ + a2η + a3ς;
y = y1 + b1ξ + b2η + b3ς;
z = z1 + c1ξ + c2η + c3ς — (I)
где а 1, а 2, а 3 суть косинусы углов, составляемых положительною осью х-ов с положительными осями ξ-ов, η-ов, ς-ов, а b1, b2, b3, c1, c2, с 3 — косинусы углов между последними и положительными осями у-ов и z-ов. Эти девять косинусов выражаются в углах θ, ψ, φ, νапример:
c3 = cosθ, b3 = sinθcosψ, a3 = sinθsinψ. Если подставить во вторые части равенств (I) вместо х 1, у 1, z1, и в косинусах а, b, с, вместо θ, ψ, φ δанные функции, то равенства эти обратятся в уравнения Д. той точки твердого тела, которой относительные координаты по отношению к осям, неизменно связанным с твердым телом, имеют постоянные величины ξ, η, ς.