Алгоритм 14 Расчет абсолютной величины разности d между эмпирическим и равномерным распределениями

1. Занести в таблицу наименования разрядов и соответствующие им эмпирические частоты (первый столбец).

2. Подсчитать относительные эмпирические частоты (частости) для каждого разряда по формуле:

f*_эмп=f_эмп/n

где f_эмп - эмпирическая частота по данному разряду;

п - общее количество наблюдений. Занести результаты во второй столбец.

3. Подсчитать накопленные эмпирические частости Σf*j по формуле:

где Σf*j=Σf*_j-1+f*_j - частость, накопленная на предыдущих разрядах; j - порядковый номер разряда; f*_j- эмпирическая частость данного /-го разряда. Занести результаты в третий столбец таблицы.

4. Подсчитать накопленные теоретические частости для каждого раз­ ряда по формуле:

Σf*_{т j}=Σf*_{Т j-1}+f*_{т j} где Σf*_{т j-1} - теоретическая частость, накопленная на предыдущих

разрядах;

j - порядковый номер разряда;

f*_{т j} - теоретическая частость данного разряда. Занести результаты в третий столбец таблицы.

5. Вычислить разности между эмпирическими и теоретическими нако­ пленными частостями по каждому разряду (между значениями 3-го и 4-го столбцов).

6. Записать в пятый столбец абсолютные величины полученных раз­ ностей, без их знака. Обозначить их как d.

7. Определить по пятому столбцу наибольшую абсолютную величину разности - d_max.

8. По Табл. X Приложения 1 определить или рассчитать критические значения d_max для данного количества наблюдений n.

Если d_max равно критическому значению d или превышает его, различия между распределениями достоверны.

Пример 2: сопоставление двух эмпирических распределений

Интересно сопоставить данные, полученные в предыдущем при­мере, с данными обследования X. Кларом 800 испытуемых (Klar H., 1974, р. 67). X. Кларом было показано, что желтый цвет является единственным цветом, распределение которого по 8 позициям не отли­чается от равномерного. Для сопоставлений им использовался метод % Полученные им эмпирические частоты представлены в Табл. 4.18.

Таблица 4.18

Эмпирические частоты попадания желтого цвета на каждую из 8 пози­ций в исследовании X. Клара (по: Klar H., 1974) (n=800)

Сформулируем гипотезы.

Н₀: Эмпирические распределения желтого цвета по 8 позициям в отечественной выборке и выборке X. Клара не различаются.

H₁: Эмпирические распределения желтого цвета по 8 позициям в отечественной выборке и выборке X. Клара отличаются друг от друга.

Поскольку в данном случае мы будем сопоставлять накопленные эмпирические частости по каждому разряду, теоретические частости нас не интересуют.

Все расчеты будем проводить в таблице по алгоритму 15.

Алгоритм 15 Расчет критерия λ при сопоставлении двух эмпирических распределений

1. Занести в таблицу наименования разрядов и соответствующие им эмпирические частоты, полученные в распределении 1 (первый столбец) и в распределении 2 (второй столбец).

2. Подсчитать эмпирические частости по каждому разряду для распределения 1 по формуле:

f*_э=f_э/n₁

где f_э - эмпирическая частота в данном разряде;

п₁ - количество наблюдений в выборке. Занести эмпирические частости распределения 1 в третий столбец.

3. Подсчитать эмпирические частости по каждому разряду для распределения 2 по формуле:

f*_э=f_э/n₂

где f_э - эмпирическая частота в данном разряде;

n₂ - количество наблюдений во 2-й выборке.

Занести эмпирические частости распределения 2 в четвертый столбец таблицы.

4. Подсчитать накопленные эмпирические частости для распределения 1 по формуле:

где Σf*_j-1 - частость, накопленная на предыдущих разрядах;

j - порядковый номер разряда;

f*_j-1- частость данного разряда.

Полученные результаты записать в пятый столбец.

5. Подсчитать накопленные эмпирические частости для распределения 2 по той же формуле и записать результат в шестой столбец.

6. Подсчитать разности между накопленными частостями по каждому разряду. Записать в седьмой столбец абсолютные величины разностей, без их знака. Обозначить их как d.

7. Определить по седьмому столбцу наибольшую абсолютную величину разности

8. Подсчитать значение критерия λ по формуле:

где п₁ - количество наблюдений в первой выборке;

n₂ - количество наблюдений во второй выборке.

9. По Табл. XI Приложения 1 определить, какому уровню статистической зна- чимости соответствует полученное значение λ.

Если λ_эмп>1,36, различия между распределениями достоверны.

Последовательность выборок может быть выбрана произвольно, так как расхождения между ними оцениваются по абсолютной величине разностей. В нашем случае первой будем считать отечественную выбор­ку, второй - выборку Клара.

Таблица 4.19

Расчет критерия при сопоставлении эмпирических распределений желтого цвета в отечественной выборке (n₁=102) и выборке Клара (n₂=800)

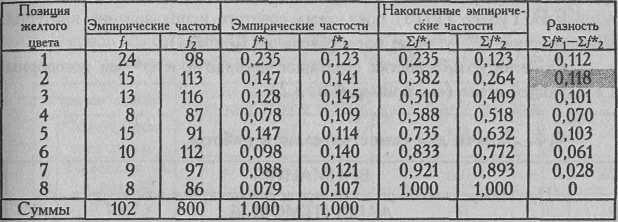
Максимальная разность между накопленными эмпирическими частостями составляет 0,118 и падает на второй разряд.

В соответствии с пунктом 8 алгоритма 15 подсчитаем значение Я,:

По Табл. XI Приложения 1 определяем уровень статистической значимости полученного значения: р=0,16

Построим для наглядности ось значимости.

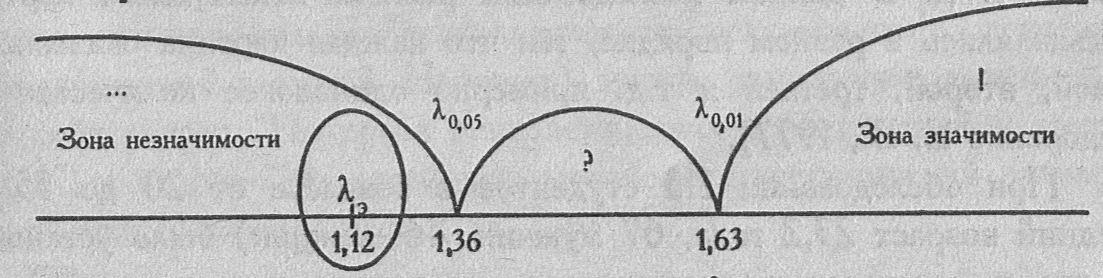
На оси указаны критические значения λ, соответствующие принятым уровням значимости: λ_0,05=1,36, λ_0,01=1,63.

Зона значимости простирается вправо, от 1,63 и далее, а зона незначимости - влево, от 1,36 к меньшим значениям.

λ_эмп>λ_кр

Ответ: Н₀ принимается. Эмпирические распределения желтого цвета по 8 позициям в отечественной выборке и выборке X. Клара совпадают. Таким образом, распределения желтого цвета в двух выбор-ках не различаются, но в то же время они по-разному соотносятся с равномерным распределением: у Клара отличий от равномерного рас­пределения не обнаружено, а в отечественной выборке различия обна­ружены (ρ<0,05). Возможно, картину могло бы прояснить применение другого метода?

Е.В. Гублер (1978) предложил сочетать использование критерия λ, с критерием φ* (угловое преобразование Фишера).

Об этих возможностях сочетания методов λ и φ* мы поговорим в следующей главе (см. пример 4 п. 5.2).

4.4. Задачи для самостоятельной работы .

ВНИМАНИЕ!

При выборе способа решения задачи рекомендуется пользоваться

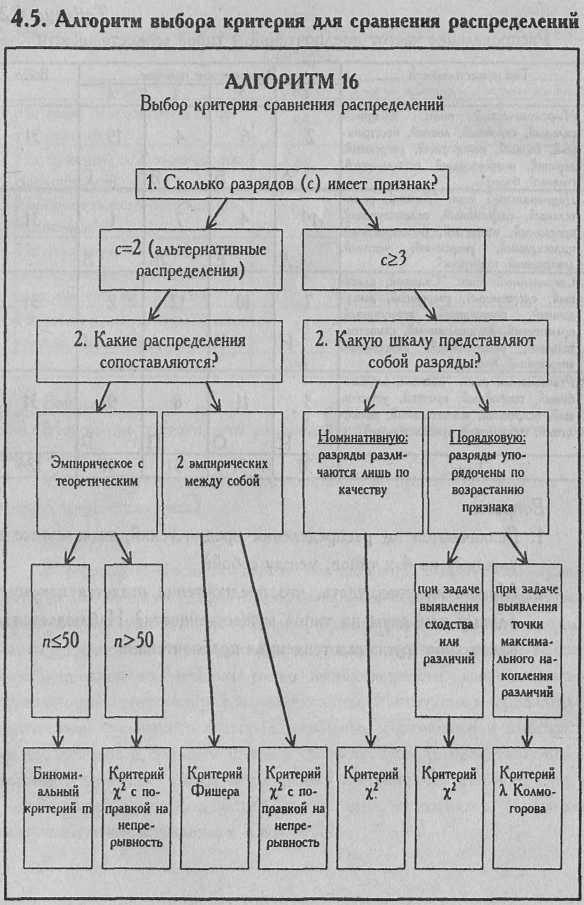
АЛГОРИТМОМ 16

Задача 6

В проективной методике X. Хекхаузена (модификация ТАТ) испытуемому последовательно предъявляются 6 картин. Всякий раз он сначала рассматривает картину в течение 20 сек, а затем в течение 5 минут пишет по ней рассказ, стараясь, в соответствии с инструкцией, проявить "максимум фантазии и воображения". После того, как испы­туемый закончит писать первый рассказ, ему предъявляется вторая кар­тина, и т. д. В данном исследовании разным испытуемым картины предъявлялись в разном порядке, так что каждая картина оказывалась первой, второй, третьей и т.д. примерно одинаковое количество раз (Сидоренко Е. В., 1977).

При обследовании 113 студентов в возрасте от 20 до 35 лет; (средний возраст 23,2 года, 67 мужчин, 46 женщин) было установле-но, что в рассказах по картинам с условными названиями "Препо-даватель и ученик" и "Мастер измеряет деталь" словесные формули­ровки, отражающие "боязнь неудачи", встречаются гораздо чаще, чем в рассказах по другим картинам, в особенности по картине "Улыбающийся юноша" (см. Табл. 4.20).

Вопросы:

1. Можно ли утверждать, что картины методики обладают разной по­ будительной силой в отношении мотивов: а) "надежда на успех"; б) боязнь неудачи"?

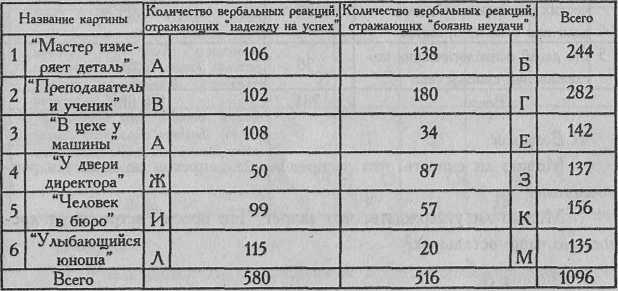
2. Как следует из Табл. 4.20, нет почти ни одной картины, которая в равной мере стимулировала бы мотив "надежда на успех" и мотив "боязнь неудачи". Можно ли считать стимульный набор методики Хекхаузена неуравновешенным по направленности воздействия?

Таблица 4.20

Эмпирическое распределение словесных формулировок, отражающих мотивы "надежда на успех" и "боязнь неудачи" (n=113)

Задача 7

В процессе проведения транзактно-аналитических сессий установ­лено, что запреты на "психологические поглаживания²¹" встречаются с неодинаковой частотой. Например, многие участники тренинга признают у себя запрет "Не проси психологических поглаживаний у других лю­дей", а запрет "Не давай психологических поглаживаний самому себе" встречается гораздо реже (см. Табл. 4.21).

Таблица 4.21

Частота встречаемости запретов на психологические поглаживания (n=166)

Вопросы:

Можно ли считать, что распределение запретов не является рав­номерным?

Можно ли утверждать, что запрет "Не проси" встречается дос­товерно чаще остальных?

Задача 8

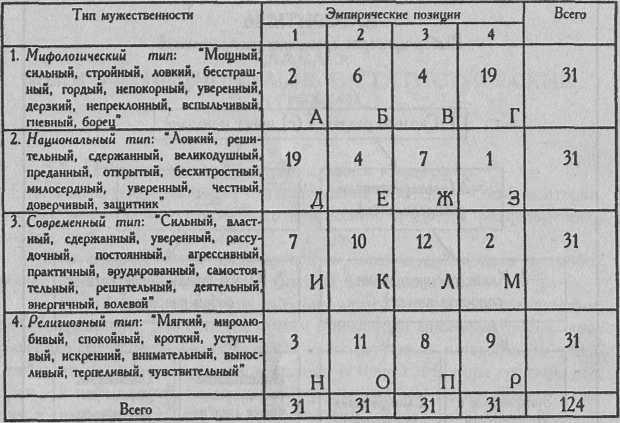
В социально-психологическом исследовании стереотипов мужест­венности Н. В. Стан (1992) выборке из 31 женщин с высшим образо­ванием в возрасте от 22 до 49 лет (средний возраст 35 лет) предъяв­лялись напечатанные на отдельных карточках перечни качеств, характе­ризующих один из четырех типов мужественности: мифологический, национальный, современный и религиозный. Испытуемым предлагалось внимательно ознакомиться с предложенными описаниями и выбрать из них то, которое в большей степени соответствует их представлению об идеальном мужчине. Затем испытуемым предлагалось выбрать одну из 3 оставшихся карточек, а затем одну из двух оставшихся. Результаты эксперимента представлены в Табл. 4.22.

Таблица 4.22

Распределение частот предпочтений 4 типов мужественности

Вопросы:

1. Различаются ли распределения предпочтений, выявленные по каждому из 4-х типов, между собой?

2. Можно ли утверждать, что предпочтение отдается какому-то одному или двум из типов мужественности? Наблюдается ли какая-либо групповая тенденция предпочтений?