
Лекция 13
Понятие игры двух лиц - антагонистической и с нулевой суммой. Схема классификации игр.
Игра
- это сложный объект
 ,
в котором
,
в котором множества и
множества и - вещественно-значные функции, i=1,...,n.
Элементы множества
- вещественно-значные функции, i=1,...,n.
Элементы множества называются стратегиями i-го игрока, а
функция
называются стратегиями i-го игрока, а
функция - функцией выигрыша i-го игрока,
- функцией выигрыша i-го игрока,
i=1,...,n.
Каждый элемент
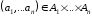 называется
реализацией игры, а число
называется
реализацией игры, а число -
выигрышем
i-го игрока, i=1,...,n в игре
-
выигрышем
i-го игрока, i=1,...,n в игре .
.
Если
n=2, то говорят об игре двух лиц. Если в
игре двух лиц
 ,
т.е. у игроков нет общих стратегий, то
игра называется антагонистической.
Если в антагонистической игре двух лиц
множества стратегий конечны, то и игра
называется конечной. Наконец, если сумма
функций выигрыша
,
т.е. у игроков нет общих стратегий, то
игра называется антагонистической.
Если в антагонистической игре двух лиц
множества стратегий конечны, то и игра
называется конечной. Наконец, если сумма
функций выигрыша ,
то конечная антагонистическая игра
двух лиц называется игрой с нулевой
суммой.
,
то конечная антагонистическая игра
двух лиц называется игрой с нулевой
суммой.
Именно
такие игры (если не будет оговорок) мы
будем рассматривать. Пусть
 - множества стратегий первого и второго
игроков, соответственно. Положим
- множества стратегий первого и второго
игроков, соответственно. Положим ,
считая, что
,
считая, что и
и и введем матрицу
и введем матрицу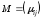 ,
которая называется «платежной матрицей
игры». Если положить
,
которая называется «платежной матрицей
игры». Если положить ,
причем в первом векторе «1» стоит на
месте № i, а во втором - на месте № j, то
окажется выполненным равенство:
,
причем в первом векторе «1» стоит на
месте № i, а во втором - на месте № j, то
окажется выполненным равенство:
 .
.
Всякий
числовой набор
 ,
в котором все
,
в котором все и сумма
и сумма ,
называется смешанной стратегией первого
игрока; аналогично, смешанной стратегией
второго игрока называется числовой
набор
,
называется смешанной стратегией первого
игрока; аналогично, смешанной стратегией
второго игрока называется числовой
набор ,
в котором все
,
в котором все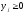 и
и .
.
Если в смешанной стратегии все координаты, кроме одной, равны нулю, то стратегия называется чистой. Всякая чистая стратегия естественным образом связана с определенной стратегией - ее номер, как элемента множества стратегий, совпадает с номером ненулевой координаты в чистой стратегии (кстати, эта ненулевая единственная координата равна, разумеется, единице).
Лекция 14
Основные характеристики игры.
В рассмотрении конечных антагонистических игр двух лиц с нулевой суммой принято, наряду с их определением, описанным выше, учитывать тот или иной принцип, которого придерживаются игроки. Ниже будут рассмотрены два таких принципа, наиболее часто встречающиеся в исследованиях и приложениях.
Принцип равной разумности. Согласно
этому принципу, оба игрока имеют равные
возможности в оценке любой ситуации и
равные возможности в использовании
этой оценки. Отметим, что элемент
 ,
будучи фиксированным, и представляет
собой «игру», так как каждый из игроков
играет, выбирая только одну какую-то
свою стратегию (с этой точки зрения
шахматы - это не игра). Реализация игры
,
будучи фиксированным, и представляет
собой «игру», так как каждый из игроков
играет, выбирая только одну какую-то
свою стратегию (с этой точки зрения
шахматы - это не игра). Реализация игры определяет выигрыш первого игрока,
который называется также проигрышем
второго игрока. Первый игрок стремится
к большему выигрышу, а второй игрок
стремится к меньшему проигрышу. Именно
это и обуславливает выбор стратегий
сторонами.
определяет выигрыш первого игрока,
который называется также проигрышем
второго игрока. Первый игрок стремится
к большему выигрышу, а второй игрок
стремится к меньшему проигрышу. Именно
это и обуславливает выбор стратегий
сторонами.
Если первый игрок выберет стратегию
 ,
то второй игрок, учитывая принцип равной
разумности, выберет ту из своих стратегий,
при которой выигрыш будет минимальным;
поэтому первому игроку имеет смыл
выбирать ту из своих стратегий, при
которой этот минимум окажется максимальным;
это означает, что число
,
то второй игрок, учитывая принцип равной
разумности, выберет ту из своих стратегий,
при которой выигрыш будет минимальным;
поэтому первому игроку имеет смыл
выбирать ту из своих стратегий, при
которой этот минимум окажется максимальным;
это означает, что число

является минимальным выигрышем, который может наступить в игре; оно называется нижней ценой игры.
Если второй игрок выберет стратегию
 ,
то первому игроку следует выбрать ту
из своих стратегий, при которой выигрыш
окажется максимальным; поэтому второй
игрок будет выбирать ту из своих
стратегий, при которой соответствующий
максимум окажется
,
то первому игроку следует выбрать ту
из своих стратегий, при которой выигрыш
окажется максимальным; поэтому второй
игрок будет выбирать ту из своих
стратегий, при которой соответствующий
максимум окажется
минимальным; это означает, что число

является максимальным проигрышем второго игрока; оно называется верхней ценой игры.
Можно
доказать, что всегда имеет место
соотношение:
 .
.
Если
 ,
то говорят, что игра имеет цену (которая
равна
,
то говорят, что игра имеет цену (которая
равна ),
а матрица M имеет седловую точку (это
как раз та клетка в платежной матрице,
в которой стоит элемент, равный цене
игры).
),
а матрица M имеет седловую точку (это
как раз та клетка в платежной матрице,
в которой стоит элемент, равный цене
игры).
Предположим теперь, что игра повторяется
несколько, скажем, N раз. В этом случае
о каждой из стратегий каждого из игроков
можно сказать, сколько раз именно к ней
прибегал игрок; пусть
 раз первый игрок прибегал к стратегии
раз первый игрок прибегал к стратегии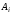 и пусть
и пусть раз второй игрок прибегал к стратегии
раз второй игрок прибегал к стратегии ,
так что
,
так что
 .
Тогда наборы
.
Тогда наборы и
и ,
где
,
где

представляют собой объекты, которые выше были названы смешанными стратегиями игроков. Тем самым становится ясным смысл смешанной стратегии - это список частот, с которыми игрок обращается к своим стратегиям при многократном повторении игры.
Можно доказать, что всегда имеют место следующие соотношения:
 .
.
Более
того, среди смешанных стратегий
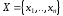 и
и есть такие, на которых достигается
следующее точное равенство:
есть такие, на которых достигается
следующее точное равенство:
 .
.
В этом состоит основная теорема теории игр. Общее значение частей последнего равенства называется ценой игры; те смешанные стратегии, при которых это равенство достигается, называются оптимальными смешанными стратегиями.
Сформулируем, в заключение знаменитую
теорему об активных стратегиях. Словами
активная стратегия обозначают такую
стратегию игрока, к которой он прибегает
хотя бы один раз, реализуя свою оптимальную
смешанную стратегию. Говоря более
формально, стратегия
 называется
активной, если в оптимальной смешанной
стратегии
называется
активной, если в оптимальной смешанной
стратегии число
число отлично
от нуля.
отлично
от нуля.
Теорема об активных стратегиях. Если первый игрок придерживается своей оптимальной смешанной стратегии, а второй игрок придерживается какой-либо своей активной стратегии, то средний выигрыш первого игрока остается равным цене игры.
Л И Т Е Р А Т У Р А
[1] Конспект лекций.
[2] Харари Ф. Теория графов. “Мир”. М.-1995.
[3] Кристофидес Н. Теория графов. “Мир”. М.-1993.
[4] Феллер В. Введение в теорию вероятностей и ее приложения. “Мир”. М.-1990.
[5] Воробьев Н.Н. Основы теории игр. “Наука”. М.-1996.
[6] Михалевич В.С., Кукса А.М. Методы последова-тельной оптимизации. “Наука”. М.-1990.
[7] Ахо А., Хопкрофт Дж., Ульман Дж. Построение и анализ вычислительных алгоритмов. “Мир”. М.-1991.
